Лабораторная работа №3

Дисциплина: Вычислительная математика

Выполнил студент гр. 3530901/80003 П. М. Курняков

Преподаватель В. Н. Цыган

“___” ___________2020 г.

Санкт-Петербург

2020

Задание

Привести дифференциальное уравнение:

к системе двух дифференциальных уравнений первого порядка.

Начальные условия: y|_t=1=2; y '|_t=1=1.

Точное решение: y(t)=

Диапазон для t: [1,2].

Решать с шагом h, используя:

1. программу RKF45

2. метод Эйлера-Коши

3. метод Адамса 3й степени точности

4. метод Рунге-Кутты 4й степени точности

Шаг h: 0.1, 0.05, 0.025, 0.0125.

Сравнить результаты, полученные заданными приближенными способами, с точным решением. Исследовать влияние размера шага на погрешность методов.

Метод решения

Код программы будем писать на языке Python.

Для начала приведем уравнение к системе дифференциальных уравнений первого порядка. Затем проведем вычисления, используя программу RKF45, используя библиотеку SciPy. Далее посчитаем то же самое остальными методами, которые были написаны самостоятельно. Метод Адамса для старта использует метод RK4. Т.к. метод Адамса не самостартующий, для преодоления больших погрешностей, перед началом работы мы, с помощью функции RK4 просчитываем значения 2 точек левее точки старта и саму точку старта. Затем уже, на основании этих данных, вычисляются с большей точностью дальнейшие точки.

Расчетные соотношения для метода Эйлера-Коши: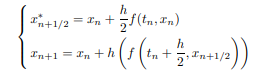

Для метода Адамса 3й степени точности:

Для метода Рунге-Кутты 4го порядка:

Произведя расчеты, получим систему дифференциальных уравнений первого порядка:

Для выполнения задания был использован язык Python и следующие библиотеки:

Функция pick_step возвращает массив точек t и точных значений в этих точках y(t):

Функция f (t, y(t)).

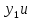
В массиве Y хранятся начальные условия и , в массиве dY - значения на нулевой и первой позиции соответственно.

Функция, вычисляющая точное решение системы:

Первый способ решения. Программа rkf45 с шагом печати h_print = 0.1 и погрешностью atol = 0.0001. Интегрирование осуществляется при помощи функции , которая возвращает настраиваемый объект, при помощи которого можно решать произвольные системы . Этот объект нужно настроить на использование методов Рунге-Кутта при помощи параметра . Соответственно, можно вызвать в некоторой точке для того, чтобы вычислить значение исследуемой функции в ней.

Функция rkf45 принимает в качестве параметров 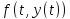, набор точек , в которых нужно вычислить значения и начальные условия . Результатом является массив значений в точках .

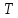Второй способ. Метод Рунге-Кутты 4 степени.

В двумерном массиве Y содержатся попарно значения в соответствующих точках. В массиве Y0 хранятся начальные условия.

Третий способ. Метод Адамса 3 степени точности

Суть методов Адамса в пошаговом вычислении значений решения 

y = y(t) дифференциального уравнения вида y’ = f (t, y). Использование трёх точек и полинома 2-й степени приведёт к формуле, представленной в расчетных соотношениях в начале отчета.

Данный метод имеет 3-ю степень точности и является явным.

Методы Адамса не являются самостартующими, т. е. они требуют для начала интегрирования специальных стартовых алгоритмов для расчета дополнительных начальных условий.

В двумерном массиве Y хранятся значения функции и производные . Чтобы вычислить начальные условия для «старта» метода Адамса, был использован метод Рунге-Кутты 4 степени. С его помощью были получены значения функции f в точках 0.8 и 0.9. Они были сохранены на нулевую и первую позицию массива Y, на второй позиции - начальное условие для точки 1.0. Затем была применена сама формула для вычисления интеграла. Значения в точках 0.8 и 0.9 не относятся к нужному промежутку решений [1;2], поэтому значения из Y были перезаписаны в Y2, начиная с 3 элемента.

Четвертый способ. Метод Эйлера-Коши.

Исторически первым и наиболее простым способом численного решения задачи Коши для ОДУ первого порядка является метод Эйлера. В его основе лежит аппроксимация производной отношением конечных приращений зависимой (y) и независимой (x) переменных между узлами равномерной сетки.

Главная функция, запускающая все методы и строящая графики:

Результаты

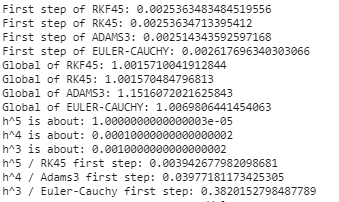
Для шага 0.1:

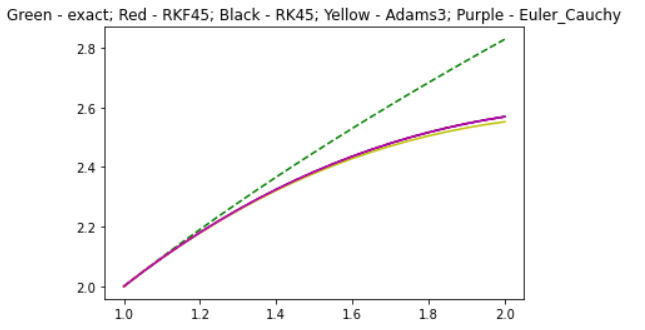
Для шага 0.05:

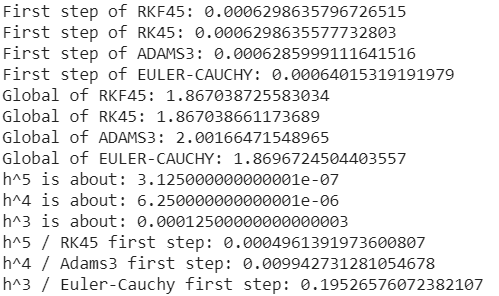
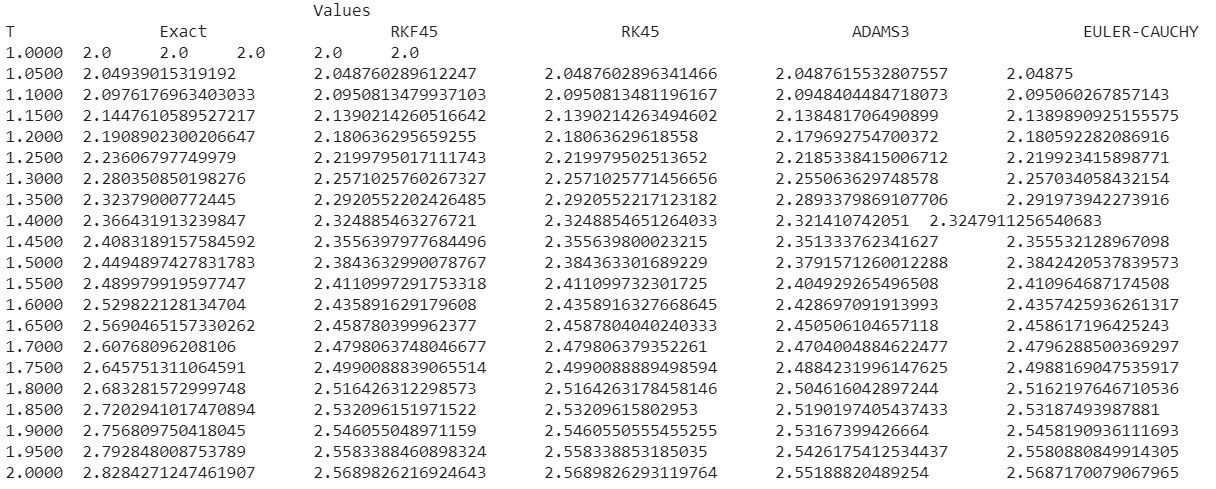
Для шага 0.025

Для шага 0.0125

Список конкретных значений слишком велик, я его опущу.

Вывод

В ходе данной работы были получены решения исходного дифф.уравнения в различных точках с помощью 4-х методов на интервале [1;2]. Решения, полученные с помощью программы rkf45, метода Рунге-Кутты 4 степени и метода Эйлера-Коши оказались самыми точными, однако при уменьшении шага итерирования метод Адамса приблизился к ним по точности.