
- •Классификация систем распознавания речи
- •Наиболее распространенный подход к распознаванию речи
- •Лекция 2
- •Цифровой звук и частота дискретизации
- •Ключевые операции цос
- •Формы преобразования Фурье
- •Б. Амплитудно-фазовая форма
- •В. Комплексная форма
- •А. Прореживание по времени
- •Вейвлет-разложение как способ представления речевого сигнала
- •Лекция 3
- •Методы представления речевого сигнала на основе кепстрального анализа и кодирования с линейным предсказанием
- •Лекция 4
- •Процесс речеобразования и принципы восприятия речи
- •Образование и артикуляционная классификация звуков речи
- •Психоакустические принципы восприятия речи
- •Признаки распознавания
- •Временные и спектральные характеристики, используемые для классификации звуков речи
- •Лекция 5
- •Выделение речи из звукового сигнала (vad-алгоритмы)
- •Сегментация речевого сигнала
- •Лекция 6
- •Применение скрытых марковских моделей для распознавания речи
- •Решение задачи 1, распознавание
- •Решение задачи 2. Алгоритм Витерби
- •Решение задачи 3. Алгоритм Баума-Уэлча.
- •Лекция 7
- •Гауссовы смешанные модели (gmm)
- •Распознавание речи с помощью нейронных сетей
- •Введение в нейронные сети
- •Лекция 8
- •Метод нелинейного растяжения-сжатия оси времени
Вейвлет-разложение как способ представления речевого сигнала
Рассмотрим
сигнал как значения непрерывной функции
времени
 .
Очевидно, что
- локализована, т. е. f
.
Очевидно, что
- локализована, т. е. f
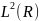 .
.
Если
конструировать базис функционального
пространства
с помощью непрерывных масштабных
преобразований и переносов вейвлета
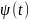 с произвольными значениями базисных
параметров – масштабного коэффициента
a и параметра сдвига
b:
с произвольными значениями базисных
параметров – масштабного коэффициента
a и параметра сдвига
b:
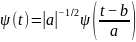 ,
a,b
R,
,
,
a,b
R,
,
то на его основе можно записать интегральное вейвлет-преобразование
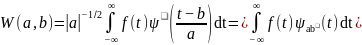
Результатом вейвлет-преобразования сигнала является двумерный массив амплитуд - значений коэффициентов W(a,b) [102-104, 106]. Распределение этих значений в пространстве (a,b) = (временной масштаб, временная локализация) дает информацию об эволюции относительного вклада компонент разного масштаба во времени и называется вейвлет-спектром.
Введя аналог
частоты
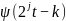 ,
где j и k
– целые числа, с помощью дискретных
масштабных преобразований
,
где j и k
– целые числа, с помощью дискретных
масштабных преобразований
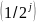 и сдвигов
и сдвигов
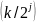 мы можем описать все частоты и покрыть
всю ось, имея единственный базисный
вейвлет
.
мы можем описать все частоты и покрыть
всю ось, имея единственный базисный
вейвлет
.
Если вейвлет
 имеет единичную норму, то все вейвлеты
семейства
имеет единичную норму, то все вейвлеты
семейства
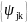 вида
вида
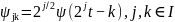
также нормированы на единицу, т. е.
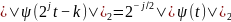
Вейвлет называется ортогональным, если семейство представляет собой ортонормированный базис функционального пространства .
Вейвлеты покрывают все пространство, используя смещение по-разному сжатых вариантов единственной функции, следовательно, любую функцию из можно разложить в вейвлет-ряд
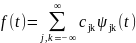
Признаки вейвлета
Для практического применения важно знать признаки, которыми обязательно должна обладать функция, чтобы быть вейвлетом:
Локализация. Вейвлет должен быть локализован и во временном пространстве, и по частоте.
Нулевое среднее:
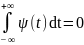
Часто для
приложений оказывается необходимым,
чтобы первые
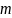 моментов
были равны 0:
моментов
были равны 0:
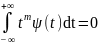
Такой вейвлет называется вейвлетом -го порядка. Обладающие большим числом нулевых моментов вейвлеты позволяют, игнорируя наиболее регулярные полиномиальные составляющие сигнала, анализировать мелкомасштабные флуктуации и особенности высокого порядка.
Ограниченность:
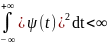
Опишем сигнал в терминах вейвлет-преобразования при помощи его средних (по некоторым интервалам) значений и изменений вокруг этих средних (флуктуациями). Это позволит вскрыть флуктуационную структуру сигнала на разных масштабах, что приводит к понятию многомасштабного анализа.
Многомасштабный анализ
Многомасштабное
приближение
представляет собой нарастающую
последовательность
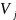 замкнутых линейных пространств
со следующими свойствами:
замкнутых линейных пространств
со следующими свойствами:
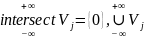 всюду
плотно в
;
всюду
плотно в
;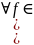 и
и
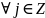
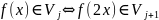 ;
;и
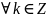
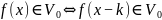 ;
;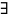 такая функция
такая функция
 что последовательность
что последовательность
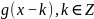 является ортонормальным базисом Рисса
в пространстве
является ортонормальным базисом Рисса
в пространстве
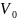 .
.
С учетом многомасштабного анализа разложение функции в вейвлет-ряд имеет вид:
 (2.14)
(2.14)
при этом
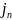 является уровнем детализации,
является уровнем детализации,
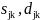 -
коэффициенты вейвлет-разложения,
-
коэффициенты вейвлет-разложения,
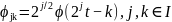 ,
,
 - скейлинг-функция или масштабная
функция,
,
- скейлинг-функция или масштабная
функция,
,
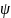 - базисный или «материнский» вейвлет.
Эти коэффициенты зачастую называют
суммами (
- базисный или «материнский» вейвлет.
Эти коэффициенты зачастую называют
суммами (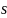 )
и разностями (
)
и разностями (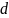 ),
связывая со средними значениями и
флуктуациями соответственно.
),
связывая со средними значениями и
флуктуациями соответственно.
Возвращаясь
к вейвлетам, отметим, что
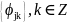 образуют ортонормированный базис
образуют ортонормированный базис
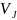 ;
;
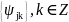 образуют ортонормированный базис в
образуют ортонормированный базис в
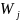 ,
где
- ортогональное дополнение
в
,
где
- ортогональное дополнение
в
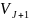 .
Полный набор
.
Полный набор
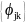 и
при всех
и
при всех
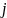 образуют ортонормированный базис в
.
образуют ортонормированный базис в
.
Вейвлет-коэффициенты
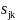 и
и
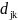 можно вычислить по формулам:
можно вычислить по формулам:
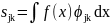 (2.15)
(2.15)
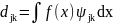 (2.16)
(2.16)
Первая сумма
в (1) со скейлинг-функциями
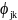 содержит
средние значения
по диадным интервалам
содержит
средние значения
по диадным интервалам
 (усреднение проводится с весовыми
функциями
,
отличными от нуля только на
-том
отрезке). Второй член содержит все
флуктуации
по данным интервалам. Эти флуктуации
проистекают из всех меньших интервалов,
заключенных внутри данного и соответствующих
большим значениям параметра масштабирования
.
Этот член фокусирует наше внимание на
все более тонких деталях изучаемого
сигнала. На любом уровне детализации
общее число членов в разложении остается
неизменным и равным
(усреднение проводится с весовыми
функциями
,
отличными от нуля только на
-том
отрезке). Второй член содержит все
флуктуации
по данным интервалам. Эти флуктуации
проистекают из всех меньших интервалов,
заключенных внутри данного и соответствующих
большим значениям параметра масштабирования
.
Этот член фокусирует наше внимание на
все более тонких деталях изучаемого
сигнала. На любом уровне детализации
общее число членов в разложении остается
неизменным и равным
 ,
где
,
где
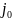 - начальный уровень с наименьшими
интервалами, число членов в каждой сумме
зависит от выбранного уровня разрешения.
На
-том
уровне имеется
- начальный уровень с наименьшими
интервалами, число членов в каждой сумме
зависит от выбранного уровня разрешения.
На
-том
уровне имеется
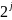 -коэффициентов
и
-коэффициентов
и
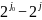 -
коэффициентов.
-
коэффициентов.
Представление
(2.14) взаимно однозначно для любой функции
из
,
т.е. коэффициенты преобразования
определяются единственным образом для
заданного вейвлет-базиса и функция
может быть полностью восстановлена по
коэффициентам разложения. На самом
детальном уровне остаются только
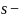 коэффициенты
и получается представление скейлинг-функцией,
конечное представление улавливает все
флуктуации, имеющиеся в сигнале. При
практическом анализе сигналов скейлинг-
и вейвлет-функции называют широкополосными
и узко-полосными фильтрами, т. к. они
отфильтровывают компоненты сигнала на
больших и малых масштабах.
коэффициенты
и получается представление скейлинг-функцией,
конечное представление улавливает все
флуктуации, имеющиеся в сигнале. При
практическом анализе сигналов скейлинг-
и вейвлет-функции называют широкополосными
и узко-полосными фильтрами, т. к. они
отфильтровывают компоненты сигнала на
больших и малых масштабах.
Вейвлеты Добеши
Свяжем
функцию
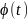 с ее сдвинутыми и сжатыми модификациями.
Простейшее линейное соотношение с
числом коэффициентов
с ее сдвинутыми и сжатыми модификациями.
Простейшее линейное соотношение с
числом коэффициентов
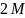 можно записать в виде:
можно записать в виде:
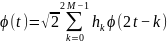
Величина
масштабирующего множителя определяет
размер ячеек выбранной решетки, число
 - число коэффициентов
- число коэффициентов
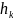 и длину области задания вейвлета. Для
ортонормированных базисов
и длину области задания вейвлета. Для
ортонормированных базисов
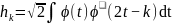
Если известна, тогда можно построить базисный вейвлет по формуле:
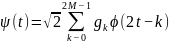 ,
где
,
где
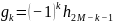 .
Связь
.
Связь
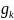 и
рассмотрим ниже.
и
рассмотрим ниже.
В практических приложениях используются только вейвлет-коэффициенты без вычисления конкретной формы вейвлета.
Общие свойства скейлинг-функций и вейвлетов однозначно определяют коэффициенты в рамках многомасштабного анализа.
Из свойства ортогональности масштабных функций:
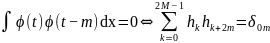 (2.17)
(2.17)
Из ортогональности вейвлетов масштабным функциям:
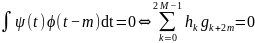
Отсюда получим
(2.18)
т. е. однозначно определяют .
Условие
ортогональности вейвлетов полиномам
до степени
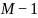 :
:
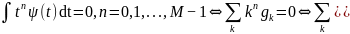 (2.19)
(2.19)
Вообще говоря, чем больше моментов равны нулю, тем больше вейвлет-коэффициентов для гладких функций близки к нулю. Очевидно, число нулевых моментов важно для достижения более сильного сжатия сигнала.
Условие нормировки:
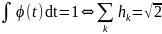 (2.20)
(2.20)
Набор всех возможностей (2.17) - (2.20) задает полную систему вейвлетов данного порядка из известного семейства ортонормальных вейвлетов Добеши. Вейвлеты Добеши с компактным носителем определяются однозначно для данного многомасштабного анализа с точностью до сдвига аргумента (смещения).
После того,
как выбран определенный вейвлет, т. е.
коэффициенты
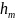 и
и
 ,
можно проводить вейвлет-преобразование
сигнала
,
поскольку задан ортонормальный
вейвлет-базис. Коэффициенты
и
из разложения (2.14) можно вычислить по
формулам (2,3). При этом компьютерные
расчеты занимают довольно длительное
время, поэтому на практике их значения
находятся с помощью быстрого
вейвлет-преобразования.
,
можно проводить вейвлет-преобразование
сигнала
,
поскольку задан ортонормальный
вейвлет-базис. Коэффициенты
и
из разложения (2.14) можно вычислить по
формулам (2,3). При этом компьютерные
расчеты занимают довольно длительное
время, поэтому на практике их значения
находятся с помощью быстрого
вейвлет-преобразования.
Быстрое вейвлет-преобразование
В реальных
ситуациях с оцифрованным сигналом мы
имеем дело с конечным набором цифр
(точек). Поэтому всегда существует
наилучший уровень разрешения, когда
каждый интервал содержит по одному
числу. Припишем значение
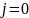 этому уровню разрешения.
этому уровню разрешения.
Многомасштабный анализ приводит естественным путем к иерархической и быстрой схеме вычисления вейвлет-коэффициентов заданной функции.
В общем случае итерационные формулы быстрого вейвлет-преобразования имеют вид:
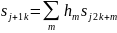
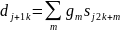
с
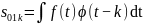 .
.
Эти уравнения
обеспечивают быстрые (так называемые
пирамидальные) алгоритмы вычисления
вейвлет-коэффициентов. Начав с
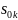 ,
мы вычислим все другие вейвлет-коэффициенты
при известных
и
.
Явный вид вейвлета при этом не используется.
Коэффициенты
по сути представляют собой локальные
средние значения сигнала, взвешенные
со скейлинг-функцией. В случае, когда
доступны только дискретные значения
,
простейшее принимаемое решение состоит
в непосредственном использовании
величин
,
мы вычислим все другие вейвлет-коэффициенты
при известных
и
.
Явный вид вейвлета при этом не используется.
Коэффициенты
по сути представляют собой локальные
средние значения сигнала, взвешенные
со скейлинг-функцией. В случае, когда
доступны только дискретные значения
,
простейшее принимаемое решение состоит
в непосредственном использовании
величин
 из доступного набора данных в виде
коэффициентов
.
из доступного набора данных в виде
коэффициентов
.
