
- •Классификация систем распознавания речи
- •Наиболее распространенный подход к распознаванию речи
- •Лекция 2
- •Цифровой звук и частота дискретизации
- •Ключевые операции цос
- •Формы преобразования Фурье
- •Б. Амплитудно-фазовая форма
- •В. Комплексная форма
- •А. Прореживание по времени
- •Вейвлет-разложение как способ представления речевого сигнала
- •Лекция 3
- •Методы представления речевого сигнала на основе кепстрального анализа и кодирования с линейным предсказанием
- •Лекция 4
- •Процесс речеобразования и принципы восприятия речи
- •Образование и артикуляционная классификация звуков речи
- •Психоакустические принципы восприятия речи
- •Признаки распознавания
- •Временные и спектральные характеристики, используемые для классификации звуков речи
- •Лекция 5
- •Выделение речи из звукового сигнала (vad-алгоритмы)
- •Сегментация речевого сигнала
- •Лекция 6
- •Применение скрытых марковских моделей для распознавания речи
- •Решение задачи 1, распознавание
- •Решение задачи 2. Алгоритм Витерби
- •Решение задачи 3. Алгоритм Баума-Уэлча.
- •Лекция 7
- •Гауссовы смешанные модели (gmm)
- •Распознавание речи с помощью нейронных сетей
- •Введение в нейронные сети
- •Лекция 8
- •Метод нелинейного растяжения-сжатия оси времени
А. Прореживание по времени
Разделим
последовательность
,
состоящую из
отсчетов, на две подпоследовательности
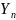 и
и
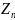 ,
каждая из N/2
отсчетов (рис.5.3).
,
каждая из N/2
отсчетов (рис.5.3).
Отсчеты образованы из четных отсчетов исходной последовательности , а отсчеты - из нечетных:
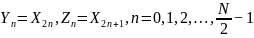 .
.
Поскольку подпоследовательности и состоят из N/2 отсчетов каждая, ДПФ для них имеет вид:
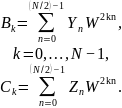
Нам нужна последовательность , которую мы можем представить через четные и нечетные элементы исходной последовательности :
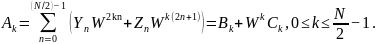


Рис.2.3 Рис.2.4
Поскольку
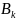 и
и
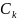 периодичны с периодом
периодичны с периодом
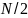 ,
можем записать:
,
можем записать:
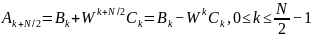 .
.
Таким
образом, первые
и последние
отсчетов ДПФ от
могут быть получены комбинацией отсчетов
ДПФ двух подпоследовательностей
и
.
На рис.2.4 представлен сигнальный граф,
наглядно представляющий процедуру
конструирования отсчетов
из отсчетов
и
для случая
 .
.


Рис.2.5 Рис.2.6
Поскольку нам удалось задачу вычисления N-точечного ДПФ редуцировать к задаче вычисления двух N/2-точечных ДПФ, естественно попытаться “развить” успех в данном направлении. На рис.2.5 и 2.6 показаны два следующих аналогичных шага, после которых отсчеты сигнала оказываются связанными с коэффициентами ДПФ своеобразными нитями-операциями, похожими на своеобразную «бабочку».
Итак,
для случая N = 23
= 8 вычисления совершаются в 3 этапа.
На первых двух этапах вычисляются некие
“промежуточные” массивы из 8 точек
каждый. На третьем этапе вычисляется
“окончательный” 8-точечный массив. Для
вычисления каждого элемента этих 3-х
массивов необходимо выполнить одно
комплексное умножение и одно
комплексное сложение – итого
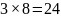 комплексных умножений и сложений вместо
комплексных умножений и сложений вместо
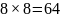 комплексных умножений и сложений при
“лобовых” вычислениях.
комплексных умножений и сложений при
“лобовых” вычислениях.
Обобщая наши рассуждения на случай N-точечных массивов, заключаем, что для вычислений в соответствии с алгоритмом БПФ необходимо N log2N комплексных умножений и сложений, тогда как при прямых вычислениях требуется N операций.
Таким образом, при прореживании по частоте, как и при прореживании по времени, процедуру вычислений делят на log2N этапов. При этом на каждом этапе на вычисление элементов N-точечного массива затрачивается N комплексных сложений и умножений. В результате вычисления производятся примерно за N log2N комплексных сложений и умножений против N 2 при “лобовых” вычислениях.
Частотно-временное представление сигнала
Частотно-временное
представление сигнала получается при
использовании оконных функций (окон)
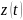 ,
обеспечивающих локализацию во времени.
Такое преобразование называется оконным
преобразованием Фурье, или
Фурье-преобразованием на коротком
интервале (STFT)
- мгновенным спектром.
,
обеспечивающих локализацию во времени.
Такое преобразование называется оконным
преобразованием Фурье, или
Фурье-преобразованием на коротком
интервале (STFT)
- мгновенным спектром.
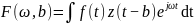 ,
,
Таким
образом,
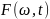 - разложение сигнала по семейству функций
- разложение сигнала по семейству функций
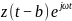 ,
образованному из единственной функции
,
образованному из единственной функции
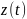 с помощью переносов
с помощью переносов
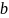 во времени и переносов
во времени и переносов
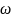 по частоте
.
по частоте
.
Частотно-временное представление сигнала, обеспечивающее локальную информацию о сигнале, как в частотной, так и во временной области. При этом сигнал делится на множество однородных маленьких участков длиной в N отсчетов (возможно, с перекрытием). Данные отрезки называют окнами или фреймами.
В настоящее время предложено большое число различных окон: прямоугольное, треугольное окно Барлета, окно Ганна, Хэмминга, Блекмана, Кайзера и ДР. Простейшим из них является прямоугольное, соответствующее умножению сигнала на константу.
Набор мгновенных спектров образует спектрограмму сигнала (Рис.2.7).
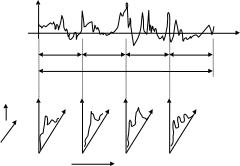
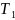
амплитуда
частота
время
Рис.2.7
При
этом невозможно достичь произвольно
хорошей локализации и по частоте и по
времени в силу принципа неопределенности
Гейзенберга. Разрешение по частоте и
по времени ограничиваются неравенством:
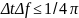 .
.
Разрешающая
способность по частоте такого спектрального
анализа определяется величиной
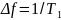 ,
а разрешающая способность по времени
– величиной
,
если сегменты анализируемого процесса
не перекрываются. Если же сегменты
перекрываются, то разрешение по времени
может быть равным даже
,
а разрешающая способность по времени
– величиной
,
если сегменты анализируемого процесса
не перекрываются. Если же сегменты
перекрываются, то разрешение по времени
может быть равным даже
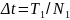 ,
где
- число отсчетов сегмента, подвергаемый
преобразованию Фурье (число
часто называют поэтому параметром БПФ
и принимают равным степени 2). Однако на
практике степень перекрытия выбирают
из неких “разумных” предпосылок,
поскольку при чересчур высокой степени
перекрытия объем вычислений может стать
неприемлемо высоким.
,
где
- число отсчетов сегмента, подвергаемый
преобразованию Фурье (число
часто называют поэтому параметром БПФ
и принимают равным степени 2). Однако на
практике степень перекрытия выбирают
из неких “разумных” предпосылок,
поскольку при чересчур высокой степени
перекрытия объем вычислений может стать
неприемлемо высоким.
Один и тот же термин “спектрограмма” применяют как к комплексной функции частоты и времени, так и к ее модулю (набору амплитудных спектров).
Пусть: x - массив отсчетов исходного сигнала размером 4001; Fs= 7418 - частота дискретизации сигнала (Рис.2.8).

Рис.2.8.
Массив B - набор амплитудных спектров вычисляется по следующим параметрам: N1 - длина окна для взвешивания сегментов сигнала (например, Бартлетта протяженностью N1=512 отсчетов); количество перекрывающихся отсчетов сегментов (например, 256). Уровень значений этих амплитудных спектров кодируется цветом. Можно наблюдать следующую спектрограмму, состоящую (при данных значениях параметров) из 14 спектров сегментов (рис.2.9)

Рис.2.9
Нетрудно
подсчитать, что длительность анализируемого
сигнала составляет
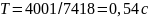 ,
диапазон анализируемых частот равен
[0,Fs/2],
т.е. [0, 3709]Гц.
,
диапазон анализируемых частот равен
[0,Fs/2],
т.е. [0, 3709]Гц.
Для
N1 = 512 получаем, что длительность
сегмента равна
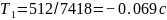 ,
разрешающая способность по частоте
составляет
,
разрешающая способность по частоте
составляет
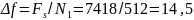 Гц.
Для степени перекрытия 256 отсчетов
разрешение по времени составляет
Гц.
Для степени перекрытия 256 отсчетов
разрешение по времени составляет
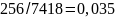 с.
с.
