
- •Классификация систем распознавания речи
- •Наиболее распространенный подход к распознаванию речи
- •Лекция 2
- •Цифровой звук и частота дискретизации
- •Ключевые операции цос
- •Формы преобразования Фурье
- •Б. Амплитудно-фазовая форма
- •В. Комплексная форма
- •А. Прореживание по времени
- •Вейвлет-разложение как способ представления речевого сигнала
- •Лекция 3
- •Методы представления речевого сигнала на основе кепстрального анализа и кодирования с линейным предсказанием
- •Лекция 4
- •Процесс речеобразования и принципы восприятия речи
- •Образование и артикуляционная классификация звуков речи
- •Психоакустические принципы восприятия речи
- •Признаки распознавания
- •Временные и спектральные характеристики, используемые для классификации звуков речи
- •Лекция 5
- •Выделение речи из звукового сигнала (vad-алгоритмы)
- •Сегментация речевого сигнала
- •Лекция 6
- •Применение скрытых марковских моделей для распознавания речи
- •Решение задачи 1, распознавание
- •Решение задачи 2. Алгоритм Витерби
- •Решение задачи 3. Алгоритм Баума-Уэлча.
- •Лекция 7
- •Гауссовы смешанные модели (gmm)
- •Распознавание речи с помощью нейронных сетей
- •Введение в нейронные сети
- •Лекция 8
- •Метод нелинейного растяжения-сжатия оси времени
Формы преобразования Фурье
Непрерывное преобразование Фурье
Известно несколько форм представления ряда Фурье:
синусно-косинусная;
амплитудно-фазовая;
комплексная.
А. Синусно-косинусная форма
Функция
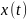 - периодическая с периодом
- периодическая с периодом
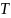 .
«Классическая» синусно-косинусная
форма представления этой функции в виде
ряда Фурье имеет вид:
.
«Классическая» синусно-косинусная
форма представления этой функции в виде
ряда Фурье имеет вид:
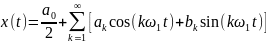 ,
(2.7)
,
(2.7)
где
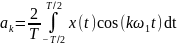 ,
,
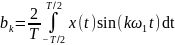 .
.
Здесь
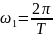 - «основная» частота ряда частот
- «основная» частота ряда частот
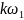 гармоник, на которые раскладывается
сигнал
.
гармоник, на которые раскладывается
сигнал
.



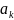
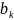
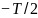 0
0
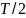
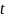 0 1 2 3
0 1 2 3
 0 1 2 3
0 1 2 3
Достоинство такого представления – вещественность величин и .
Недостаток
– не очень понятна необходимость функций
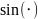 и
и
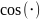 .
.
Б. Амплитудно-фазовая форма
Запишем (2.7) в виде:
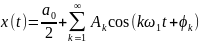 .
(5.2)
.
(5.2)
Или, что то же,
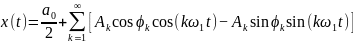 .
.
Сравнивая с (5.1), видим, что:
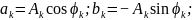
откуда
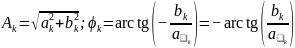 .
.
В. Комплексная форма
В амплитудно-фазовой форме полагаем:
 .
.
Получаем:
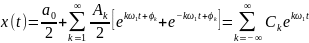 ;
(2.8а)
;
(2.8а)
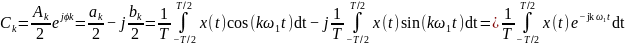 (2.8б)
(2.8б)
Дискретное преобразование Фурье
Пару непрерывных преобразований Фурье обычно записывают в виде:
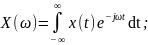 (2.9а)
(2.9а)
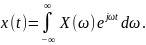 (2.9б)
(2.9б)
Перепишем соотношения (2.8) в виде:
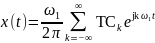 ;
;
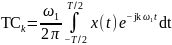 .
.
При
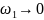 эти соотношения превращаются в пару
непрерывных преобразований Фурье,
поэтому:
эти соотношения превращаются в пару
непрерывных преобразований Фурье,
поэтому:
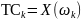 (2.10)
(2.10)
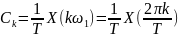 .
.
Можно рассуждать и по-иному. Сравним соотношения:
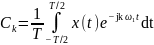 ;
;
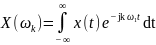 .
.
Если
функция
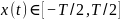 ,
тогда, периодизируя ее, можем записать:
,
тогда, периодизируя ее, можем записать:
, что совпадает с полученным ранее соотношением (2.8).
Таким образом, с учетом соотношений (2.6) и (2.8) можем записать:
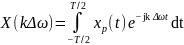 ;
(2.11а)
;
(2.11а)
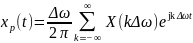 ,
(2.11б)
,
(2.11б)
где
обозначено
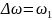 .
Сравнивая пары соотношений (2.9) и (2.11),
видим, что пару (5.6) можно формально и
абсолютно точно получить, заменяя в
(2.9а) бесконечные пределы интегрирования
на конечные, а в (2.9б) – заменяя интеграл
суммой. Причина точности произведенной
замены – периодическое продолжение
функции времени, приводящее к дискретизации
спектра. Чтобы подчеркнуть периодический
характер функции времени, мы и применили
обозначение
.
Сравнивая пары соотношений (2.9) и (2.11),
видим, что пару (5.6) можно формально и
абсолютно точно получить, заменяя в
(2.9а) бесконечные пределы интегрирования
на конечные, а в (2.9б) – заменяя интеграл
суммой. Причина точности произведенной
замены – периодическое продолжение
функции времени, приводящее к дискретизации
спектра. Чтобы подчеркнуть периодический
характер функции времени, мы и применили
обозначение
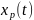 .
.
Используя дуальность времени t и частоты f, а также полученный выше результат о возможности формального перехода от пары непрерывных преобразований Фурье к паре дискретно-непрерывных преобразований Фурье, сразу запишем:
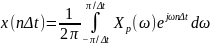 ;
(2.12а)
;
(2.12а)
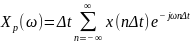 ,
(2.12б)
,
(2.12б)
Продолжая развивать идею «дискретизации-периодизации», приходим к паре дискретных соотношений:
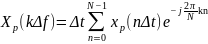 ;
;
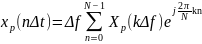 ,
где
,
где
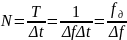 .
.

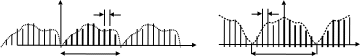
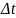
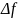

0 -
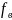
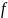
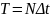
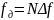
Обозначая
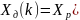 ,
получим «классическую» пару дискретных
преобразований Фурье (ДПФ):
,
получим «классическую» пару дискретных
преобразований Фурье (ДПФ):
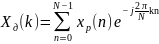 ;
(2.13а)
;
(2.13а)
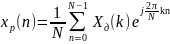 (2.13а)
(2.13а)
Быстрое преобразование Фурье (БПФ)
Пару ДПФ часто записывают в виде:
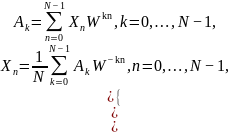
где
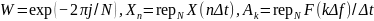 ,
,
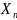 - отсчеты сигнала,
- отсчеты сигнала,
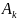 - коэффициенты ДПФ.
- коэффициенты ДПФ.
Для
вычисления одного элемента последовательности
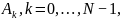 необходимо примерно
операций комплексных умножений и
сложений, если вычисления производить
«в лоб», т.е. в соответствии с приведенным
выше соотношением. БПФ – это «хитроумная»
схема вычислений, при которой количество
вычислительных операций удается сделать
существенно меньшим. Например, если N
- степень двойки, тогда количество
вычислительных операций пропорционально
величине
необходимо примерно
операций комплексных умножений и
сложений, если вычисления производить
«в лоб», т.е. в соответствии с приведенным
выше соотношением. БПФ – это «хитроумная»
схема вычислений, при которой количество
вычислительных операций удается сделать
существенно меньшим. Например, если N
- степень двойки, тогда количество
вычислительных операций пропорционально
величине
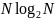 .
Преимущества алгоритма БПФ быстро
увеличиваются с ростом N,
что существенно при обработке массивов
большой размерности.
.
Преимущества алгоритма БПФ быстро
увеличиваются с ростом N,
что существенно при обработке массивов
большой размерности.
Еще
более заметен выигрыш алгоритма БПФ
при обработке двумерных массивов чисел,
например, при обработке изображений. В
этом случае необходимо
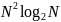 операций против
операций против
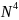 при «лобовых» вычислениях.
при «лобовых» вычислениях.
Существует несколько разновидностей алгоритма БПФ. Ниже будет изложена модификация алгоритма БПФ: с прореживанием по времени. Существует и вторая - с прореживанием по частоте. При этом рассмотрим случай, когда N - степень двойки.
