Вариант 7
Решить систему уравнений по формулам Крамера
2. Вычислить пределы функций
1)
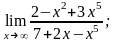2)
3)
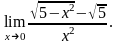
3. Вычислить производные функций
1)
;
2)
;
3)
4. Провести полное исследование функции и построить ее график
5. Вычислить неопределенный интеграл
1)
;
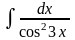2)
;
3)
.
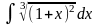6. Вычислить определенный интеграл
1)
;
2)
;
3) Вычислить площадь фигуры, ограниченной
графиками функций
,
.
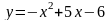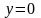7.
Даны числа
,
,
,
1. Изобразить на числовой плоскости
2. Найти модули и аргументы чисел . Записать в тригонометрической форме.
3. Вычислить , , .
Вариант 8
Решить систему уравнений по формулам Крамера
2. Вычислить пределы функций
1)
2)
3)
3. Вычислить производные функций
1)
;
2)
;
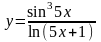3)
.
4. Провести полное исследование функции и построить ее график
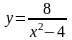
5. Вычислить неопределенный интеграл
1)
;
2)
;
3)
.
6. Вычислить определенный интеграл
1)
;
2)
;
3) Вычислить площадь фигуры, ограниченной
графиками функций
,
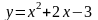7.
Даны числа
,
,
,
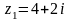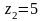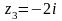1. Изобразить на числовой плоскости
2. Найти модули и аргументы чисел . Записать в тригонометрической форме.
3. Вычислить , , .
Вариант 9
Решить систему уравнений по формулам Крамера
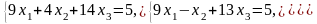
2. Вычислить пределы функций
1)
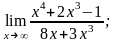2)
3)
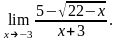
3. Вычислить производные функций
1)
;
2)
;
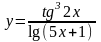3)
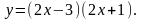
4. Провести полное исследование функции и построить ее график
5. Вычислить неопределенный интеграл
1)
;
2)
;
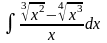3)
.
6. Вычислить определенный интеграл
1)
;
2)
;
3) Вычислить площадь фигуры, ограниченной
графиками функций
,
.
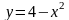7.
Даны числа
,
,
,
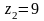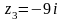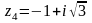
1. Изобразить на числовой плоскости
2. Найти модули и аргументы чисел . Записать в тригонометрической форме.
3. Вычислить , , .
Вариант 10
Решить систему уравнений по формулам Крамера
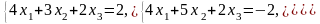
Вычислить пределы функций
1)
2)
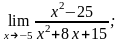3)
3. Вычислить производные функций
1)
;
2)
;
3)
.
4. Провести полное исследование функции и построить ее график
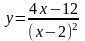
5. Вычислить неопределенный интеграл
1)
;
2)
;
3)
.
6. Вычислить определенный интеграл
1)
;
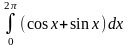2)
;
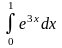3) Вычислить площадь фигуры, ограниченной
графиками функций
,
.
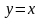7.
Даны числа
,
,
,
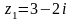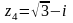
1. Изобразить на числовой плоскости
2. Найти модули и аргументы чисел . Записать в тригонометрической форме.
3. Вычислить , , .
Вопросы для подготовки к дифференцированному зачету по дисциплине «математика»
Матрицы. Виды матриц.
Действия над матрицами.
Определители 1-го, 2-го порядков.
Определители 3-го порядка. Правило треугольников.
Система линейных алгебраических уравнений. Формулы Крамера.
Предел функции в точке. Основные теоремы о пределах.
Предел функции при x стремящемся к бесконечности. Замечательные пределы.
Непрерывность функции в точке и на промежутке. Свойства непрерывных функций.
Точки разрыва функции. Классификация точек разрыва.
Производная функции.
Геометрический смысл производной.
Механический смысл производной.
Таблица производных.
Понятие сложной функции. Производная сложной функции.
Схема исследования функции. Область определения функции. Четность и нечетность функции. Нули функции. Возрастание и убывание функции, правило нахождения промежутков монотонности. Точки экстремума функции, правило нахождения экстремумов функции.
Асимптоты функции.
Первообразная. Свойства первообразной.
Неопределенный интеграл. Основные свойства неопределенного интеграла.
Таблица неопределенных интегралов.
Методы интегрирования: метод непосредственного интегрирования; метод замены переменной (метод подстановки).
Определенный интеграл. Понятие интегральной суммы.
Основные свойства определенного интеграла.
Геометрический смысл определенного интеграла.
Методы вычисления определенных интегралов. Формула Ньютона-Лейбница.
Геометрические и физические приложения определенного интеграла.
Комплексные числа. Алгебраическая и геометрическая записи комплексного числа.
Действия над комплексными числами.
Понятие события. Достоверные, невозможные, совместные, несовместные, противоположные события. Классическое определение вероятности.
Теорема сложения вероятностей. Теорема умножения вероятностей.
Случайная величина. Дискретная и непрерывная случайные величины.
Закон распределения дискретной случайной величины.
Математическое ожидание дискретной случайной величины. Отклонение случайной величины. Дисперсия дискретной случайной величины. Среднее квадратичное отклонение случайной величины.
Логические операции: отрицание, дизъюнкция, конъюнкция, строгая конъюнкция, импликация, эквиваленция.
Булевы функции.
Дифференцированный зачет проводится в форме тестирования.
Приложение 1