
- •Формулы логики высказываний
- •Логическое следствие
- •Нормальные формы.
- •Метод резолюций в логике высказываний
- •Предикаты и операции с ними. Формулы.
- •1) Атомарная формула;
- •Интерпретация, равносильность. Законы логики предикатов. Логическое следствие.
- •Нормальные формы в логике предикатов
- •Метод резолюций в логике предикатов
- •11. Языки и операции с ними
- •12. Конечный автомат. Язык, допускаемый конечным автоматом
- •13.Регулярные языки. Теорема Клини
- •14. Контекстно-свободные грамматики
Интерпретация, равносильность. Законы логики предикатов. Логическое следствие.
Опр. Вхождение переменной в формулу называется связанным, если переменная стоит непосредственно за квантором, или входит в область действия квантора по этой переменной.
Вхождение переменной свободное в противном случае.
Опр. Переменная называется свободной в формуле, если существует хотя бы одно свободное вхождение этой переменной в формулу.
Пример.
 .
.
Опр. Интерпретацией формулы F на непустом множестве M называется отображение , ставящее в соответствие:
символу константы элемент из M,
символу n-местной функции f некоторую функцию на M,
символу n-местного предиката A некоторый предикат, заданный на M.
Результатом
(F)
интерпретации формулы является предикат
,
где переменные
 являются свободными в формуле F.
являются свободными в формуле F.
Опр.
Формулы
![]() и
и
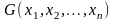 называются равносильными, если для
любой интерпретации
на множестве M,
и любых элементов
,
значения истинности высказываний
называются равносильными, если для
любой интерпретации
на множестве M,
и любых элементов
,
значения истинности высказываний
 и
и
 совпадают.
совпадают.
Опр.
Формула
 называется тождественно истинной, если
для любой интерпретации
на множестве M,
и любых элементов
,
высказывание
истинно.
называется тождественно истинной, если
для любой интерпретации
на множестве M,
и любых элементов
,
высказывание
истинно.
Теорема.


Законы логики предикатов:
1) 21) аналогичны законам логики высказываний.
22)
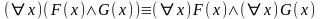 ;
;
23)
 ;
;
Замечание:
1.
![]() .
.
Для доказательства неравносильности можно привести контрпример.
Пусть
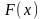 = «Число x
чётное»,
= «Число x
чётное»,
 = «Число x
нёчетное»
одноместные предикаты на N.
= «Число x
нёчетное»
одноместные предикаты на N.
Тогда и левая часть и правая часть равенства являются высказываниями:
л.ч. = «Для любого натурального числа x выполняется, что x чётное или x нечётное» = 1;
п.ч. = «Любое натуральное число чётное или любое натуральное число нечётное» = 0 0 = 0.
2.
 ;
;
Доказательством служит такая же интерпретация, как в предыдущем случае.л.ч. = «Существует натуральное число x, такое, что выполняется x чётное и x нечётное» = 0;
п.ч. = «Существует натуральное число чётное и существует натуральное число нечётное» = 1 & 1 = 1.
24)
 ;
;
25)
 ;
;
Замечание:

Для доказательства неравносильности можно привести контрпример.
Пусть
 = « x
y »
двухместный предикат на N.
= « x
y »
двухместный предикат на N.
л.ч. = «Для любого числа x существует y, превышающий или равный x» = 1.
п.ч. = «Существует число y, такое, что для любого x выполняется x y» = 0.
26)
 ;
;
27)
 ;
;
28)
 ;
;
29)
 ;
;
Пусть
 ,
не содержит y,
,
не содержит y,
 не содержит x.
не содержит x.
30)
 ;
;
31)
 ;
;
32)
 ;
;
33)
 .
.
Опр.
Формула
называется логическим следствием
формул
 ,
если для любой интерпретации
на множестве M,
и любых элементов
,
из того, что все значения
,
если для любой интерпретации
на множестве M,
и любых элементов
,
из того, что все значения
 ,
…,
,
…,
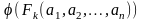 истинны, следует, что значение
истинно.
истинны, следует, что значение
истинно.
Нормальные формы в логике предикатов
Опр. Формула F
имеет предварённую нормальную форму
(ПНФ), если
 ,
где
,
где
 ,
H
не содержит кванторов.
,
H
не содержит кванторов.
Теорема.
Для всякой формулы F существует равносильная формула, имеющая ПНФ.
Доказательство:
Алгоритм приведения к ПНФ.
1. Исключить эквиваленцию и импликацию (по законам 21 и 20).
2. Занести отрицание к атомарным формулам (по законам де Моргана 17 и 18).
3. Вынести кванторы вперед, используя (если нужно) переименование переменных (по законам 22, 23, 28 33).
Опр. Формула F
имеет сколемовскую нормальную форму
(СНФ), если
 ,
где H
не содержит кванторов и имеет КНФ.
,
где H
не содержит кванторов и имеет КНФ.
Теорема.
Для всякой формулы F существует формула, имеющая СНФ, одновременно с F выполнимая или невыполнимая. Доказательство:
Алгоритм приведения к СНФ.
1, 2, 3 из алгоритма приведения к ПНФ.
Результат
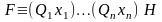 .
.
4. Бескванторную часть H привести к КНФ.
5. Исключить кванторы существования, поочередно слева направо, применяя одно из двух правил:
1 случай)
 ~
~
 ,
где a символ
константы.
,
где a символ
константы.
2 случай)
 ~
~
~
 ,
где
,
где

символ функции, зависящей от переменных
символ функции, зависящей от переменных
 .
.
При выполнении 1, 2, 3, 4 шагов алгоритма получается формула, равносильная F, следовательно, выполнимая или не выполнимая одновременно с F.
Если существует
интерпретация ,
при которой формула
истинна, то
существует значение
 ,
такое, что при этой же интерпретации
значение
,
такое, что при этой же интерпретации
значение
 истинно. Т.е.
формула
выполнима.
истинно. Т.е.
формула
выполнима.
Если существует
интерпретация ,
при которой формула
истинна,
то для любых значений переменных
 существует подходящее значение
существует подходящее значение
 ,
такое, что при этой же интерпретации
значение
,
такое, что при этой же интерпретации
значение
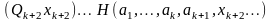 истинно. Т.е. существует функция
(
истинно. Т.е. существует функция
( ),
для которой формула
выполнима.
),
для которой формула
выполнима.
Опр.
Множество формул
 выполнимо, если существует интерпретация
на множестве M,
и существуют элементы
,
такие, что все значения
,
…,
выполнимо, если существует интерпретация
на множестве M,
и существуют элементы
,
такие, что все значения
,
…,
 истинны.
истинны.
Невыполнимо в противном случае.
Теорема.
Формула G является логическим следствием формул множество формул не выполнимо.
