1. Высказывания и операции с ними.

Опр. Высказывание  повествовательное предложение, о котором можно сказать: истинно оно или ложно.

Опр. Значение истинности высказывания  истина или ложь.

Высказывания делятся на простые и составные.

Опр. Составное высказывание получено из простых при помощи операций (связок).

конъюнкция дизъюнкция отрицание импликация эквиваленция

Опр. Конъюнкция высказываний X и Y  высказывание, полученное при помощи союза «и», т.е. «…X… и …Y…».

X & Y

Опр. Дизъюнкция высказываний X и Y  высказывание, полученное при помощи союза «или», т.е. «…X… или …Y…».

X  Y

Опр. Конъюнкция высказываний X и Y  высказывание, полученное при помощи союза «и», т.е. «…X… и …Y…».

X & Y

Опр. Дизъюнкция высказываний X и Y  высказывание, полученное при помощи союза «или», т.е. «…X… или …Y…».

X  Y

Опр. Отрицание высказывания X  высказывание, полученное при помощи приставки «не», т.е. «не …X…».

 X

Опр. Импликация высказываний X и Y  высказывание, полученное при помощи конструкции «Если …X…, то …Y…».

X  Y

Опр. Импликация высказываний X и Y  высказывание, полученное при помощи конструкции «Если …X…, то …Y…».

X  Y

Опр. Эквиваленция высказываний X и Y  высказывание, полученное при помощи конструкции «…X…, если и только если …Y…».

X  Y

2. Формулы логики высказываний

Атомарная формула логики высказываний  заглавная буква латинского алфавита, с индексом или без, а также символ 0 или 1.

Опр. Формула логики высказываний  выражение одного из двух видов:

1) атомарная формула;

2) (F & G), (F  G), (F), (F  G), (F  G),

где F и G  формулы логики высказываний.

Для уменьшения количества скобок договоримся о приоритетах операций:

		наивысший
&		средний
		низший

Примеры:

1. Формула X & Y  Z означает ((X) & Y)  Z .

2. Выражение X & Y  Z не является формулой.

4. Логическое следствие

Опр. Формула G называется логическим следствием формул , если для любой интерпретации из того, что все значения истинны, следует, что значение истинно.

Замечание. Формула G является логическим следствием формул , если .

Опр. Множество формул выполнимо, если существует интерпретация такая, что все значения истинны.

Невыполнимо  в противном случае.

Теорема.

Формула G является логическим следствием формул  множество формул не выполнимо.

4. Нормальные формы.

Опр. Литерал  атомарная формула (кроме 0 и 1), или ее отрицание.

Элементарная конъюнкция  литерал или конъюнкция литералов.

Опр. Формула F имеет дизъюнктивно-нормальную форму (ДНФ), если она является элементарной конъюнкцией или дизъюнкцией элементарных конъюнкций.

( …. & …. & … )  ( …. & …. )  ( … ) …

Теорема.

Для всякой формулы F существует равносильная формула, имеющая ДНФ.

Доказательство:

Алгоритм приведения к ДНФ.

1. Исключить эквиваленцию и импликацию (по законам 21 и 20).

2. Занести отрицание к атомарным формулам (по законам де Моргана 17 и 18).

3. К не элементарным конъюнкциям применить законы дистрибутивности (11 и 12).

Опр. Формула F имеет совершенную дизъюнктивно-нормальную форму (СДНФ) относительно атомарных формул , если:

1) в записи F участвуют только ;

2) F имеет ДНФ, т.е. ;

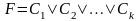3) Каждая содержит или , или , для любого j.

4) F не содержит одинаковых элементарных конъюнкций.

Теорема.

Для всякой выполнимой формулы F существует равносильная формула, имеющая СДНФ.

Доказательство:

Алгоритм приведения к СДНФ.

Алгоритм приведения к СДНФ.

1, 2, 3  из алгоритма приведения к ДНФ.

Результат  формула , равносильная исходной. 4. Если не содержит ни , ни , то заменяем на .

5. Если F содержит несколько одинаковых элементарных конъюнкций, то вычеркиваем их все, кроме одной.

Элементарная дизъюнкция  литерал или дизъюнкция литералов.

Опр. Формула F имеет конъюнктивно-нормальную форму (КНФ), если она является элементарной дизъюнкцией или конъюнкцией элементарных дизъюнкций.

( ….  ….  … ) & ( ….  …. ) & ( … ) …

Теорема.

Для всякой формулы F существует равносильная формула, имеющая КНФ.