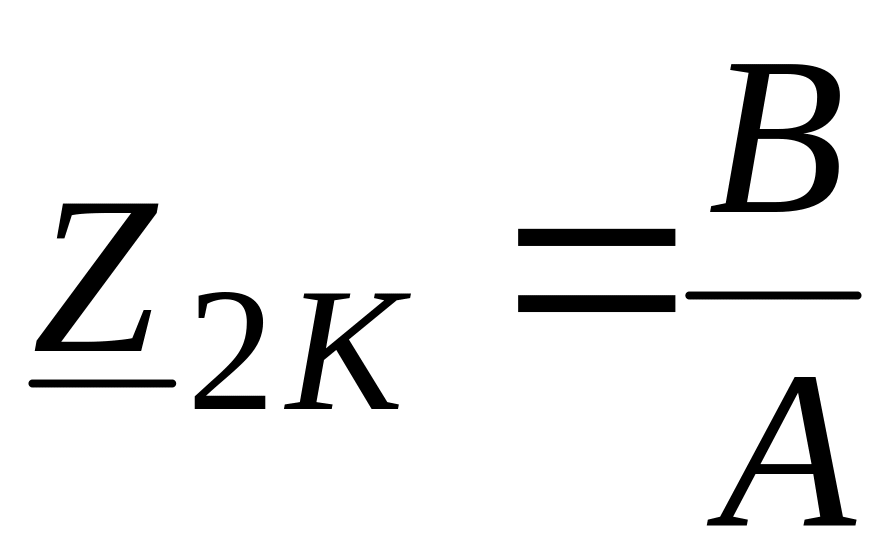Кафедра теоретической электротехники и электрических машин лаборатория теоретической электротехники Руководство к лабораторной работе № 108 «Исследование резонанса токов»

Программа работы.

1. Настройка цепи в резонанс с изменением емкости С конденсатора при постоянном значении частоты f.

2. Установка величины затухания d резонансного контура.

3. Исследование зависимостей токов , , в неразветвленной части цепи, в конденсаторе и в катушке от емкости С конденсатора, при постоянном значении напряжения на зажимах цепи.

4. Исследование зависимостей напряжения и токов , 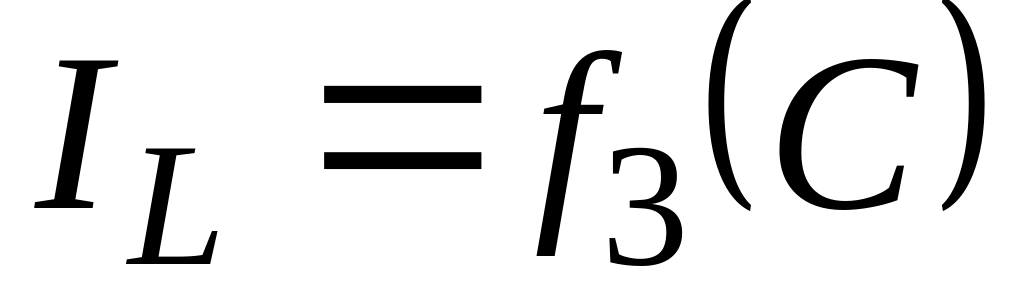в конденсаторе и катушке от емкости С конденсатора при постоянной частоте и постоянном значении тока I в неразветвленной части цепи.

5. Построение снятых характеристик в абсолютных координатах.

6. Составление отчета.

Цель работы

Исследование резонанса токов имеет целью ознакомить студентов с характером резонансных кривых в простейшей параллельной цепи и показать, что при резонансе в параллельной цепи токи в катушке и конденсаторе могут превысить ток в неразветвленной цепи.

Основные теоретические положения.

Условие резонанса в простейшей параллельной цепи (рис.1) выражается в виде равенства нулю реактивной проводимости этой цепи:

.

При резонансе полная проводимость достигает своего наименьшего значения, равного активной проводимости g и ток в цепи, если напряжение на зажимах цепи не изменяется, получает также наименьшее значение.

В условиях данной лабораторной работы настройку параллельной цепи в резонанс осуществляют изменением емкости конденсатора. Для величины конденсатора , при которой наступает резонанс, имеем:

Из векторной диаграммы токов, представленной на рис.2 при условии резонанса в цепи, видно, что токи I_L и I_C в катушке и конденсаторе могут превосходить ток в неразветвленной части цепи. Поэтому резонанс при параллельном соединении носит название резонанса токов. Из диаграммы следует, что увеличение токов в катушке и конденсаторе при резонансе, по сравнению с током в неразветвленной части цепи, будет иметь место при условии

или .

Так как , то оба эти условия приводятся к одному, а именно:

,

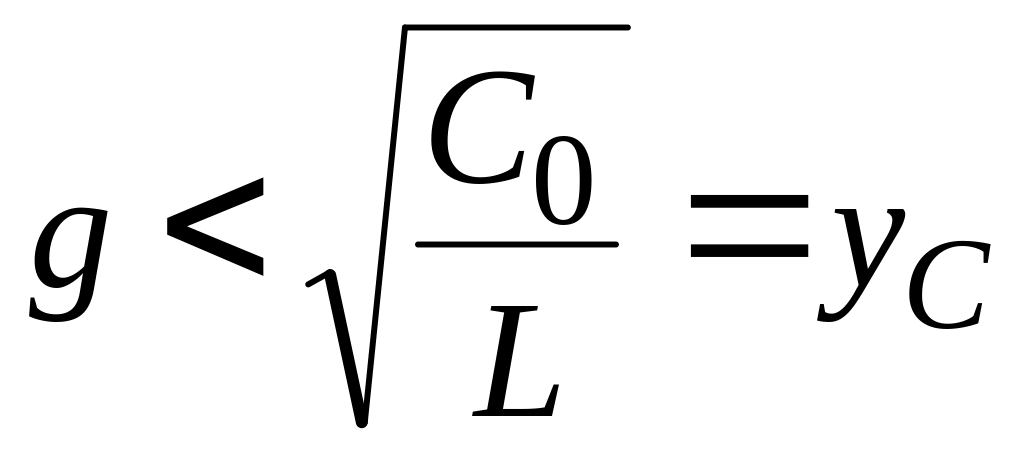где величина 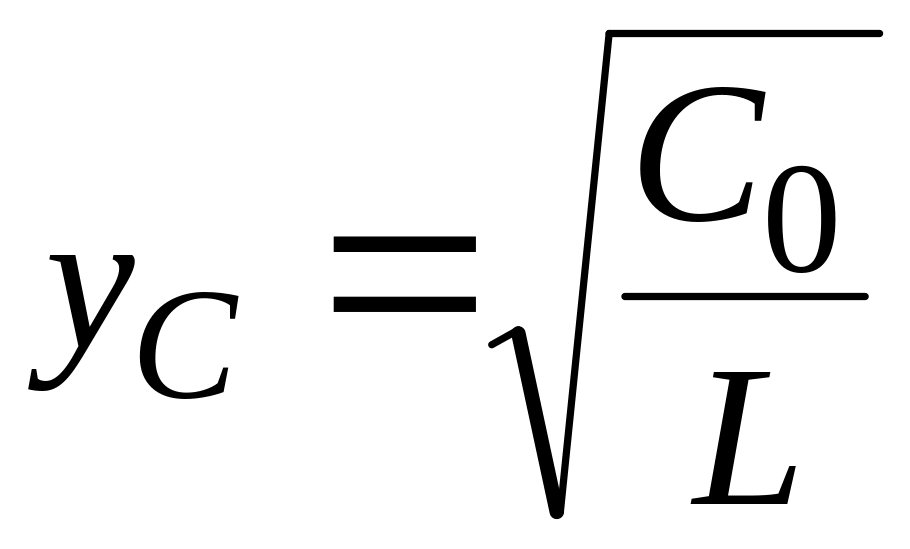, имеющая размерность проводимости, носит название волновой проводимости цепи g, L, C₀.

Используя условие резонанса, нетрудно показать, что волновая проводимость равна индуктивной проводимости катушки или емкостной проводимости конденсатора в момент резонанса:

.

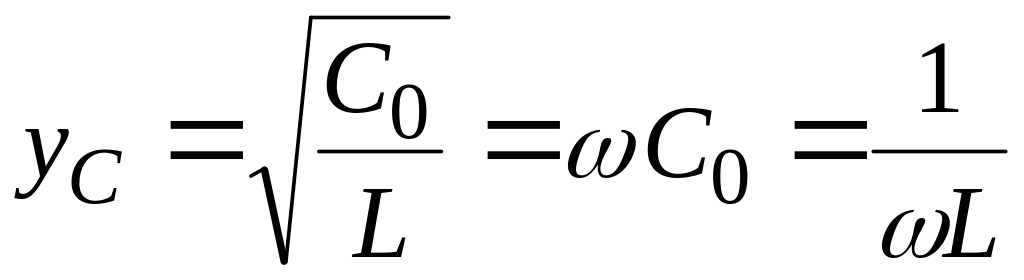Отношение называется затуханием цепи. Таким образом, условие увеличения токов при резонансе токов можно записать в виде:

.

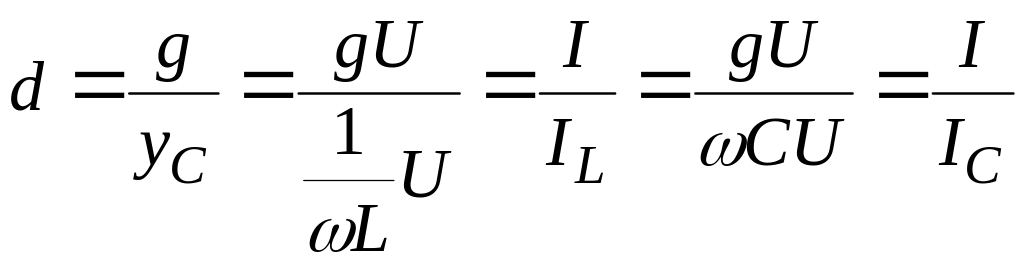Рассмотрим характер зависимостей напряжения и токов в различных участках схемы от величины емкости С конденсатора при изменении ее в обе стороны от резонансного значения.

При постоянном напряжении на зажимах цепи ток в неразветвленной части цепи, определяющийся выражением:

Будет зависеть от емкости С конденсатора так же, как зависит от нее полная проводимость y цепи, то есть будет иметь при резонансе минимальное значение. Нетрудно убедиться, что характер этой зависимости аналогичен зависимости из резонанса напряжений и представленной на рис.4.

Ток в катушке, как это видно из выражения , но будет зависеть от емкости конденсатора, а ток в конденсаторе будет расти пропорционально увеличению емкости (аналогично характеристикам и из резонансов напряжений, изображенных на рис.4.

При постоянном значении I в неразветвленной части цепи напряжение U на зажимах цепи, равное

Будет иметь в момент резонанса максимум, а общий характер зависимости напряжения U от емкости будет аналогичен зависимости из резонанса напряжений и представленной на рис.3.

Пользуясь рассуждениями, подобными тем, которыми мы пользовались при анализе резонанса напряжений, нетрудно показать, что зависимость тока

(при постоянном значении I в неразветвленной части цепи) будет подобна только что рассмотренной зависимости , а зависимость тока – аналогична зависимости из резонанса напряжений (рис.3), причем, при увеличении емкости до бесконечности, ток будет стремиться к току I в неразветвленной цепи.

Практические указания к выполнению работы.

1. Для исследования явления резонанса токов собирают схему согласно рис.5, в которой используется регулируемая емкость лабораторного стенда около 70 мкФ, а в качестве индуктивной катушки – вариометр, использованный при исследовании резонанса напряжений. При этом подвижная катушка должна быть в положении п.2б, которое соответствует резонансному значению индуктивности при резонансе напряжений.

2. Настройку цепи в резонанс осуществляют, изменяя емкость, по минимуму тока в неразветвленной части цепи. Грубо резонанс можно установить, уравнивая токи в катушке и конденсаторе. Однако это условие не является в условиях нашей работы точным, так как индуктивная катушка обладает также и некоторым активным сопротивлением.

Заданное преподавателем затухание цепи устанавливается с помощью реостата R, который течение последующего исследования должен оставаться неприкосновенным.

3. Зависимости, указанные в пунктах 3 и 4, снимают, изменяя ступенями емкость конденсаторов, причем вблизи резонанса эти ступени следует брать меньшими, а вдали от него их можно увеличить. В первом случае напряжение, а во втором – ток поддерживают с помощью автотрансформаторов.

4. Кривые, относящиеся к работе, строятся в абсолютных величинах на двух графиках, отдельно для пунктов 3 и 4.

5. Отчет составляется в соответствии с требованиями правил и методических указаний к выполнению работ и составлению отчетов.

6. Таблица результатов измерений и расчетов при постоянном напряжении на зажимах цепи.

№№ п.п.	Измерения				Расчет
	I	IL	IC	φ	C
	А	А	А		мкФ

7. Таблица результатов измерений и расчетов при постоянном токе в неразветвленной части цепи.

№№ п.п.	Измерения				Расчет
	U	IL	IC	φ	C
	В	А	А		мкФ

ЛИТЕРАТУРА:

Л.А. Бессонов – Теоретические основы электротехники, 1973 г. Стр. 135 – 137.

КАФЕДРА ТЕОРЕТИЧЕСКОЙ ЭЛЕКТРОТЕХНИКИ И ЭЛЕКТРИЧЕСКИХ МАШИН

ЛАБОРАТОРИЯ ТЕОРЕТИЧЕСКОЙ ЭЛЕКТРОТЕХНИКИ

Руководство к лабораторной работе № 109 «Исследование электрической цепи со взаимной индуктивностью»

Программа работы.

1. Определение параметров катушек вариометра и разметка конов катушек.

2. Определение взаимной индуктивности и коэффициента связи.

3. Исследование работы трансформатора без стального сердечника. Построение векторных диаграмм трансформатора. Проверка баланса мощностей.

4. Исследование режимов работы электрической цепи при параллельном соединении индуктивно-связанных катушек. Построение векторной диаграммы. Проверка баланса мощностей.

5. Составление отчета.

Цель работы:

Работа имеет целью ознакомить студентов с особенностями работы цепей с взаимной индуктивностью, с распределением токов, напряжений и мощностей в таких цепях.

Основные теоретические положения.

Если изменяющийся во времени магнитный поток одного контура электрической цепи пронизывает второй контур, то во втором контуре возникает э.д.с. взаимной индукции и при этом происходит передача мощности (энергии) из одного контура в другой через магнитное поле.

Наиболее типичным представителем магнитосвязанных контуров является трансформатор. В нем вторичная обмотка (второй контур) обычно не связаны электрически с источниками энергии и вся мощность, потребляемая в цепи вторичной обмотки, передается из первичной обмотки посредством переменного магнитного поля.

Если второй контур включен в электрическую цепь, содержащую источники энергии, то лишь часть всей потребляемой энергии он получает из первого контура через магнитное поле (или, наоборот, передает в первый).

Для электрической схемы, изображенной на рис.1, имеем:

,

,

.

Построенная по этим уравнениям векторная диаграмма токов и напряжений имеет вид, изображенный на рис.2.

Активная мощность, полученная от источника первой ветвью

.

Проекция напряжения U на направление тока I₁, то есть состоит из двух отрезков: напряжения на активном сопротивлении первой ветви I₁U₁ и проекции напряжения I₂x_M, то есть

.

Соответственно и активная мощность, получаемая первой ветвью от источника, состоит из двух слагаемых

,

т.е. первая ветвь получает от источника мощность, меньшую, чем требуется на нагрев активного сопротивления R₁ на величину

.

Эту недостающую мощность первая ветвь получает от второй ветви через магнитное поле.

Если аналогичным путем подсчитать активную мощность, получаемую от источника второй ветвью, то получим:

Вторая ветвь получает от источника мощность, большую, чем требуется на нагревание активного сопротивления R₂ на величину , т.е. именно на ту величину, которую она передает первой ветви через магнитное поле.

Общая активная мощность, получаемая обеими ветвями от источника

Если одну индуктивно связанных катушек (назовем ее первой) присоединить к источнику переменного напряжения, а зажимы второй замкнуть на вольтметр, как показано на рис.3, по данным измерений можно найти полное сопротивление первой катушки

Активное сопротивление

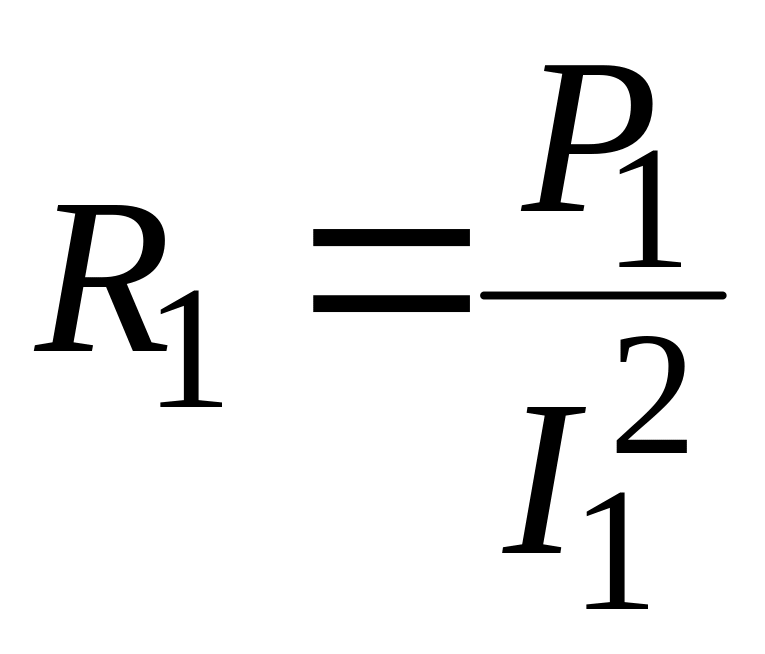
Индуктивное сопротивление

Сопротивление взаимоиндукции

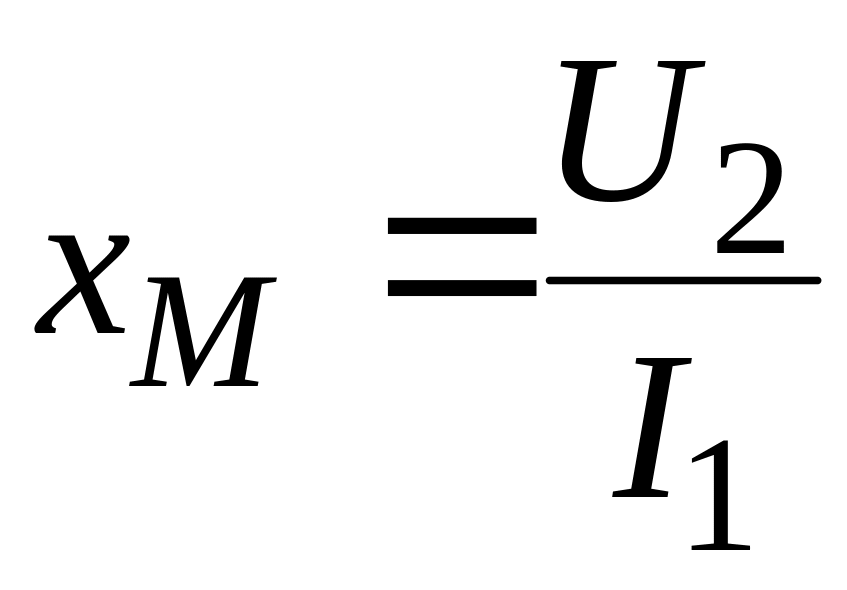
Аналогичным образом можно найти параметры второй катушки:

Коэффициент связи катушек

Практические указания к выполнению работы.

Лабораторная работа имеет два варианта, отличающихся второй частью. Бригада студентов выполняет один вариант по указанию преподавателя.

В качестве индуктивно связанных катушек используются катушки вариометра. При этом подвижная катушка должна быть полностью введена.

Первая (общая для обеих вариантов) часть работы включает пункты 1 и 2 программы работ.

1. Определение параметров катушек производится по схеме рис.3.

2. Определение общего полного сопротивления обеих последовательно соединенных катушек производится при согласном и встречном соединениях по схемам рис. 4. При этом “начало” и “конец” одной из катушек выбираются произвольно, а “начало” и “конец” другой катушки определяются по результатам измерений.

1. Вычислить сопротивление взаимной индуктивности x_M и коэффициент связи:

;

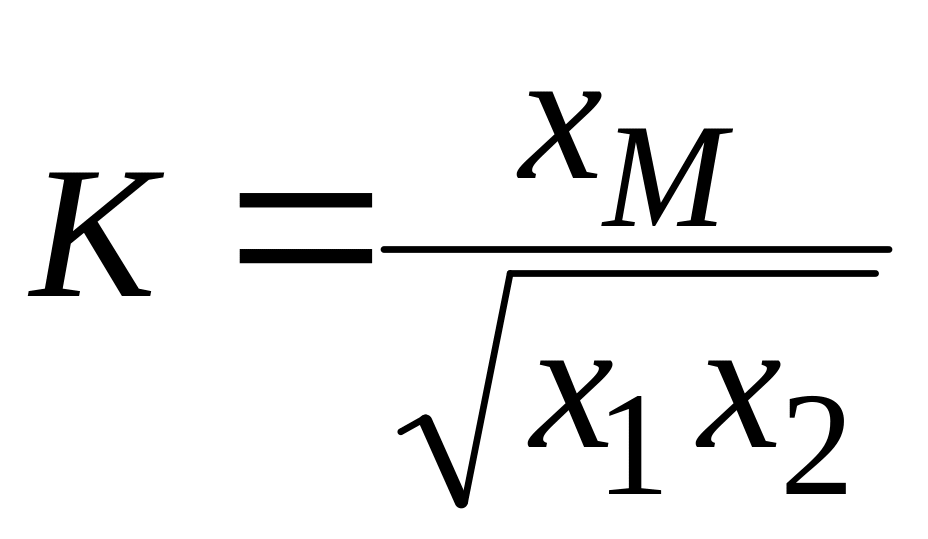
Вторая часть работы.

Первый вариант. Исследование трансформатора без стального сердечника:

1. Собрать схему, изображенную на рис. 5. При этом катушку с меньшей индуктивностью присоединить к сети, а вторичную обмотку замкнуть на активное сопротивление.

2. Поддерживая неизменным напряжение на зажимах первичной обмотки, изменять ток нагрузки от нуля (холостой ход) до наибольшей возможной величины. Записать значения измеряемых величин для 4-5 различных значений нагрузки.

3. По результатам измерений построить в масштабе векторные диаграммы токов и напряжений для холостого хода к для максимального тока нагрузки. По последней векторной диаграмме вычислить активную мощность нагрузки и мощность, передаваемую от одной обмотки к другой через магнитное поле. Вычислить потери мощности на нагревание первичной и вторичной обмоток. Сравнить их с показаниями ваттметра.

Второй вариант. Исследование параллельного соединения индуктивно связанных катушек.

4.1. Собрать схему, изображенную на рис.6. Последовательно с катушкой, имеющей меньшую индуктивность, включить активное нагрузочное сопротивление. Поддерживая неизменным напряжение на зажимах цепи, изменять сопротивление нагрузки от нуля до наибольшей величины. Записать значения измеряемых величин для 4-5 различных значений нагрузки.

4.2. При максимальном сопротивлении нагрузки измерить все три мощности одним ваттметром, отсоединяя последовательно концы параллельных ветвей от точки “в” и присоединяя их к точке “а”.

4.3. Построить по результатам измерений две векторные диаграммы: одну для сопротивления нагрузки, равноq нулю; другую для максимального сопротивления нагрузки. По последней векторной диаграмме вычислить активные мощности, получаемые каждой катушкой, и мощность, передаваемую от одной катушки к другой через магнитное поле. Сравнить эти мощности с показаниями ваттметра.

5. Отчет составляется в соответствии с “правилами и методическими указаниями к выполнению лабораторных работ и составлению отчетов.

6. Таблица результатов измерений и расчетов параметров катушек.

№№ катушек	Измерения			Расчет
	U	I	P	Z	R	X2	XM
	В	А	Вт	Ом	Ом	Ом	Ом
1-я катушка
2-я катушка

6. Таблица результатов измерений и расчетов при согласном и встречном включении катушек.

Способ включения	Измерения			Расчет
	В	А	Вт	Ом	Ом	Ом
Согласно
Встречно

6. Таблица результатов измерений и расчетов при исследовании трансформатора без сердечника.

№№ п.п.

Измерения

Расчет

В

А

Вт

В

А

В

В

В

В

В

В

В

№№ п.п.

Измерения

Расчет

В

А

Вт

А

Вт

В

А

Вт

В

В

В

В

В

В

ЛИТЕРАТУРА:

Л.А. Бессонов – Теоретические основы электротехники, 1973 г. Стр. 146 – 152.

КАФЕДРА ТЕОРЕТИЧЕСКОЙ ЭЛЕКТРОТЕХНИКИ И ЭЛЕКТРИЧЕСКИХ МАШИН

ЛАБОРАТОРИЯ ТЕОРЕТИЧЕСКОЙ ЭЛЕКТРОТЕХНИКИ

Руководство к лабораторной работе № 110 «Экспериментальное определение коэффициентов пассивного четырехполюсника и параметров схем замещения»

Программа работы.

1. Проведение опытов холостого хода и короткого замыкания.

2. Вычисление входных сопротивлений.

3. Определение коэффициентов четырехполюсника.

4. Определение параметров схем замещения пассивного четырехполюсника.

Цель работы.

Целью работы является закрепление студентами навыков экспериментального определения входных сопротивлений, определение коэффициентов пассивного четырехполюсника.

Основные теоретические положения.

Линейным пассивным четырехполюсником называется часть линейной электрической цепи, не содержащая источников энергии и имеющая два входных (1 – 1) и два выходных (2 – 2) зажима (рис.1).

Основными уравнениями четырехполюсника, связывающими ток и напряжение на входе с током и напряжением на выходе, являются уравнения:

,

.

Коэффициенты A, B, C, D в общем случае являются комплексными числами и их величины зависят от схемы внутренних соединений четырехполюсника, от значений активных сопротивлений и реактивностей схемы и от частоты.

Для заданного четырехполюсника коэффициенты A, B, C, D при неизменной частоте будут постоянными комплексными числами, связанными соотношением:

Коэффициенты A, B, C, D можно вычислить по значениям входных сопротивлений четырехполюсника, определяемых в режимах холостого хода и короткого замыкания.

Если в схеме рис.2 разомкнуть зажимы 2 – 2, то ток , и такой режим называется холостым ходом. При холостом ходе из основных уравнений четырехполюсника имеем:

,

.

Входное сопротивление четырехполюсника при холостом ходе со стороны зажимов 1 – 1:

(1).

Замкнем выходные зажимы 2 – 2 накоротко (например, через амперметр). В режиме короткого замыкания , и из уравнений четырехполюсника имеем:

,

.

Входное сопротивление четырехполюсника при коротком замыкании

(2).

Запитаем четырехполюсник со стороны зажимов 2 – 2 и проведем опыты холостого хода и короткого замыкания. Так как при такой замене в уравнениях четырехполюсника меняются местами коэффициенты A и D, то:

	(3),
	(4).

По показаниям приборов из опытов холостого хода и короткого замыкания найдем:

; ; ,

; ; ,

; ; ,

; ; .

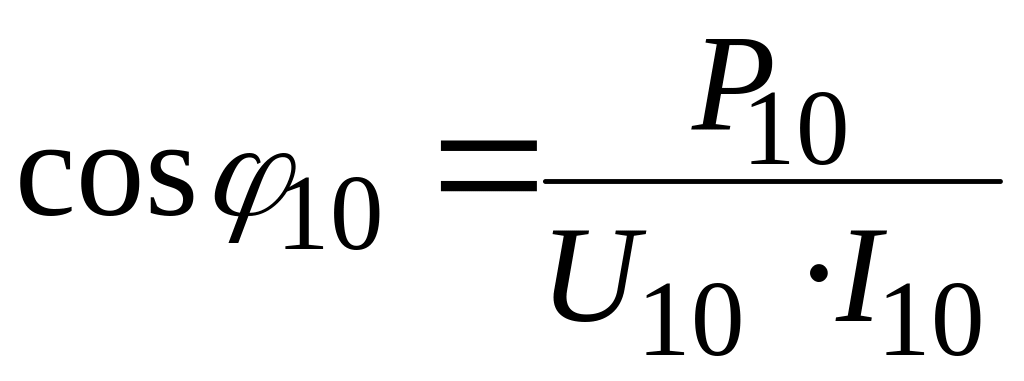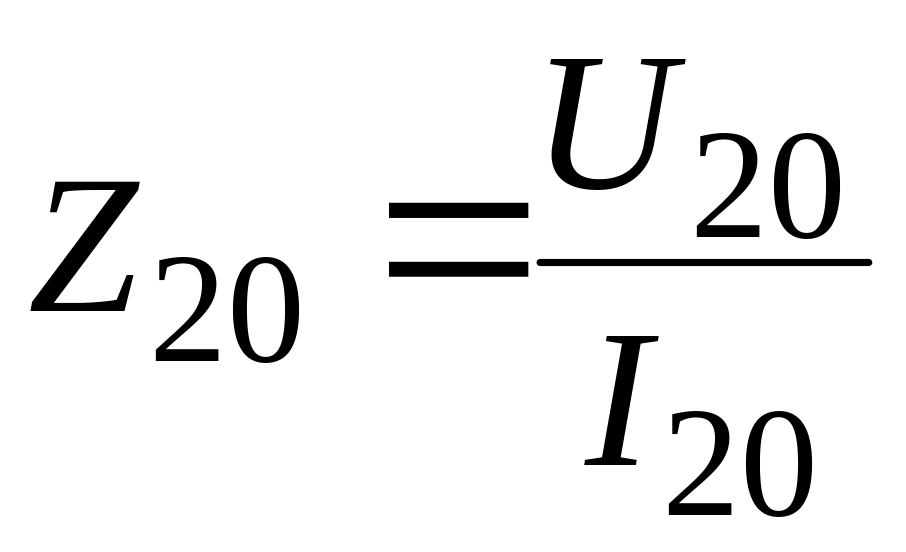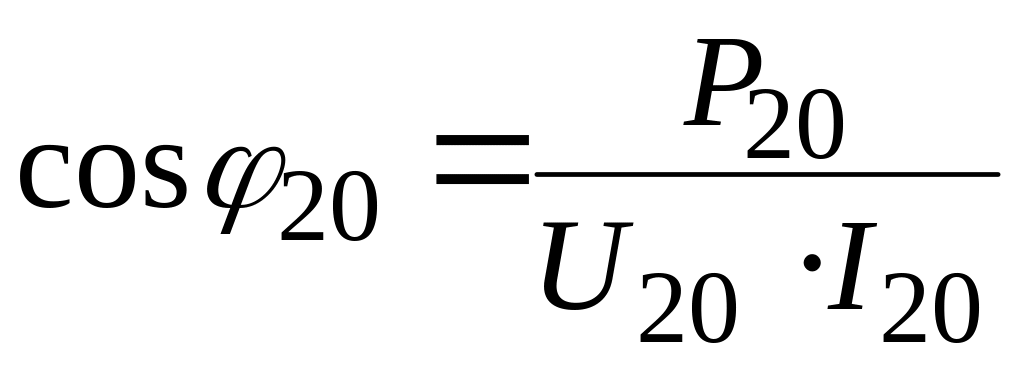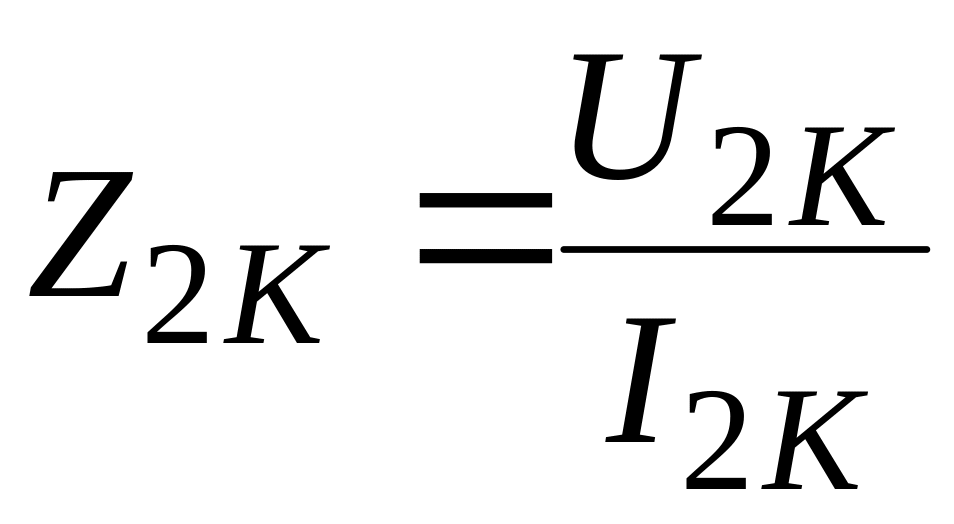Знак угла во всех опытах определяется с помощью емкости С, подключаемой параллельно четырехполюснику. Для правильного определения знака величина емкости должна выбираться из условия

.

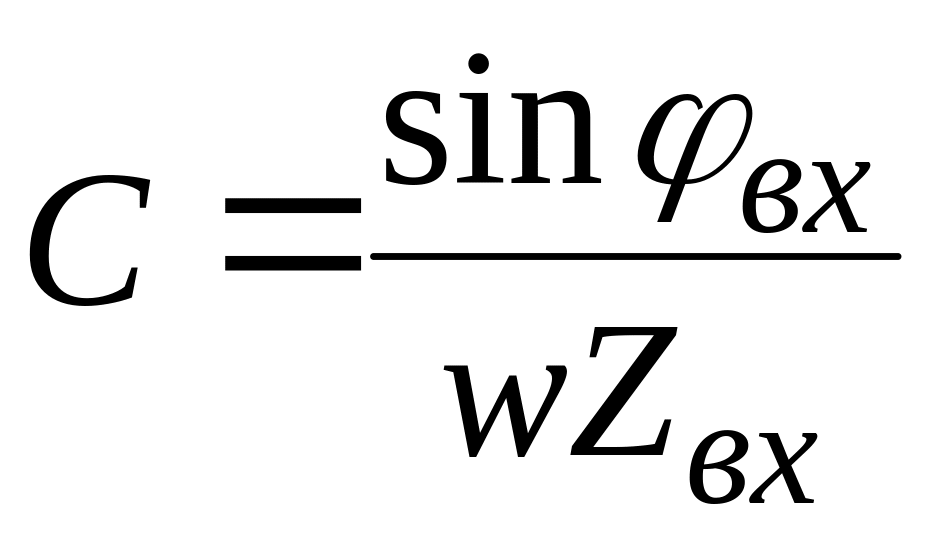Любые три из четырех значений входных сопротивлений можно использовать для нахождения коэффициентов A, B, C, D.

;

;

;

.

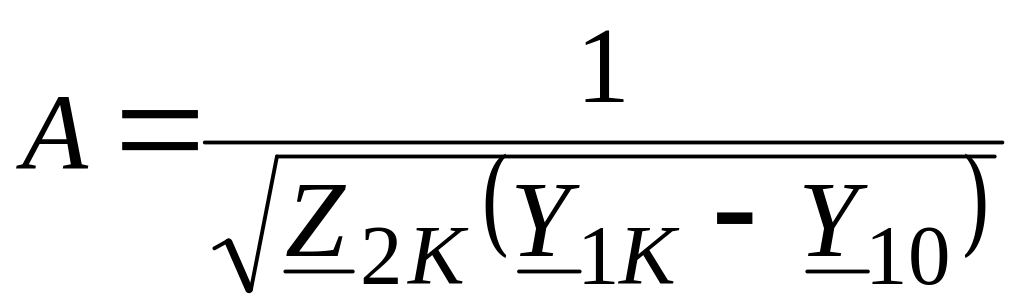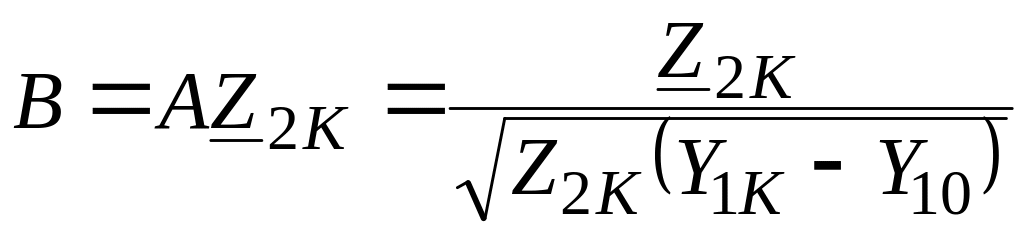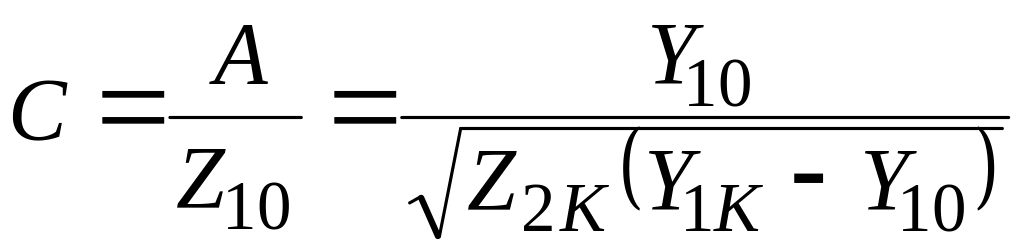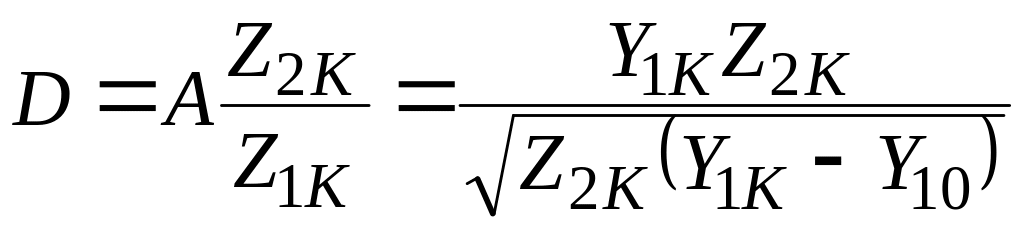Параметры схем замещения четырехполюсника определяются из известных соотношений.

Для Т-образной схемы замещения (рис.3):

;

;

.

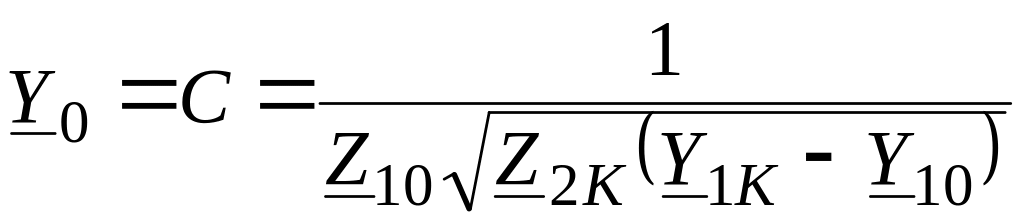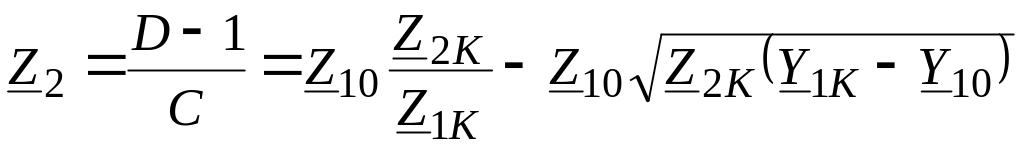Для П-образной схемы замещения (рис 4):

;

;

.

Практические указания к выполнению работы.

1. Для определения величин входных сопротивлений собирается схема рис.2. на этой схеме проводятся опыты холостого хода и короткого замыкания при питании четырехполюсника со стороны зажимов 1-1 и опыт короткого замыкания при питании четырехполюсника со сторон зажимов 2-2. Результаты наблюдений и вычислений заносятся в таблицу.

При опытах короткого замыкания напряжение питания подается такой величины, чтобы ток выходного контура не превышал 3А.

2. Величины входных сопротивлений определяются по формулам:

; ; .

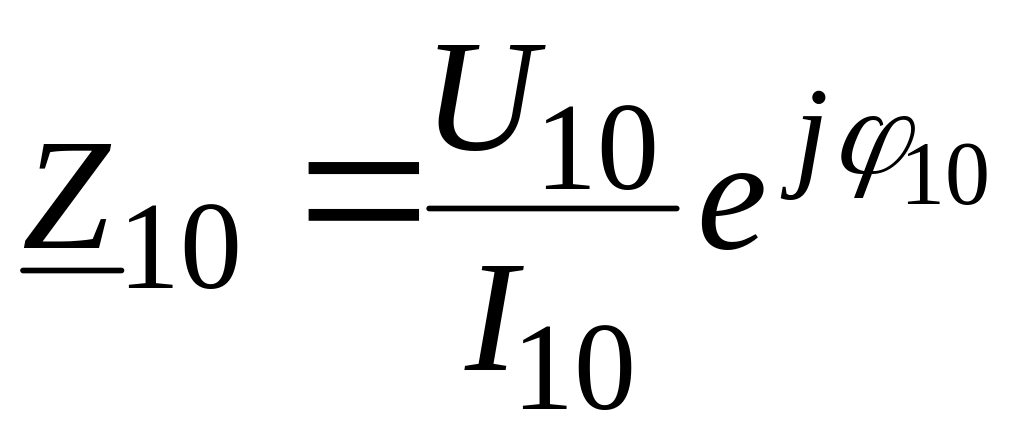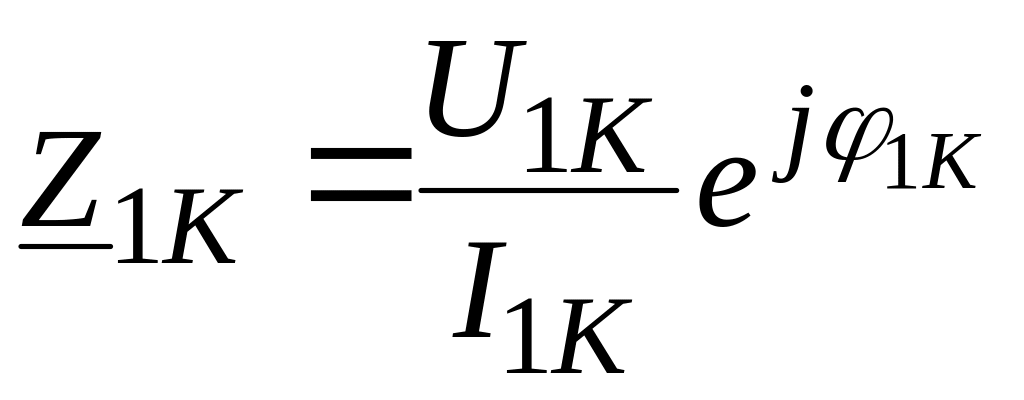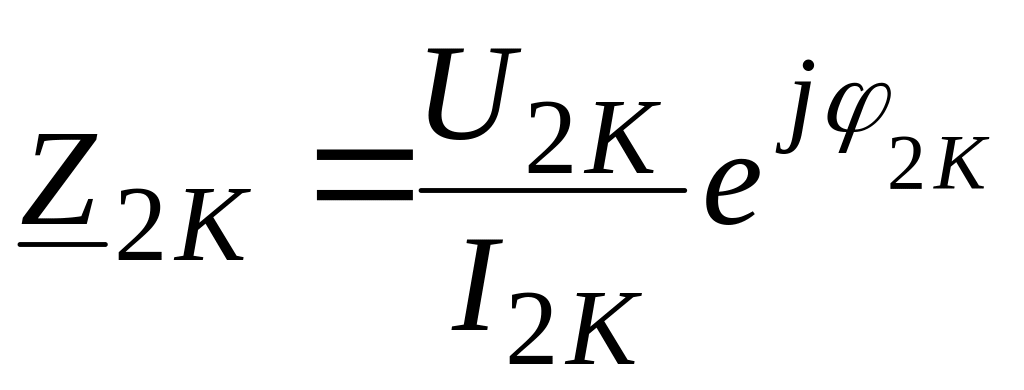3. По найденным значениям 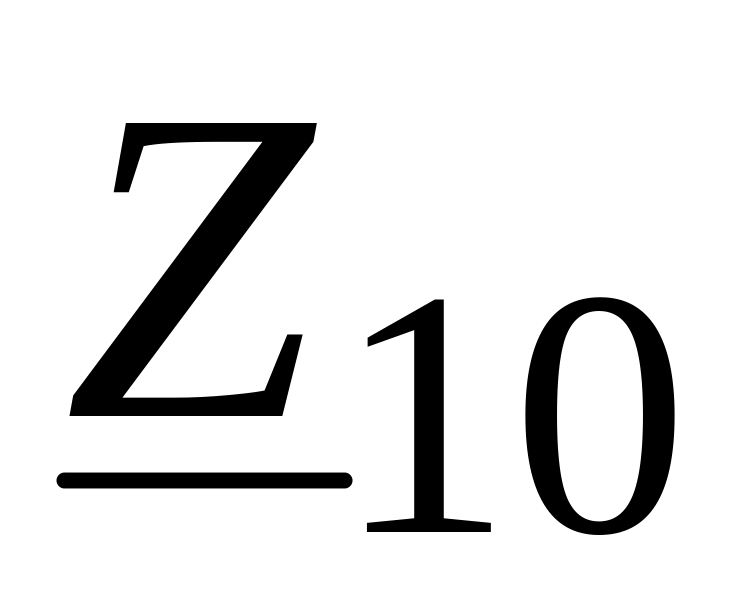, , 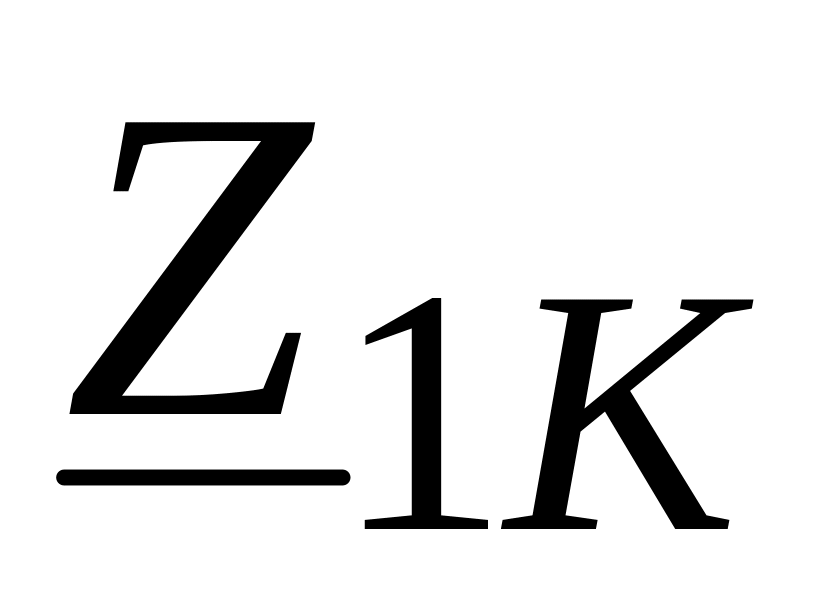подсчитываются коэффициенты A, B, C, D. Модули коэффициентов A, B и C должны быть равны соответственно значениям:

; ; .

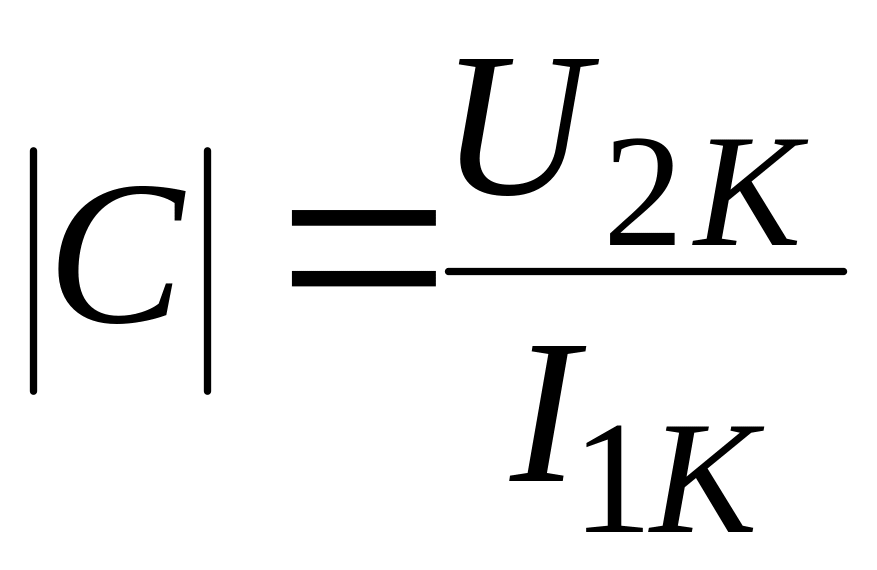4. Определяются параметры схем замещения четырехполюсника.

5. Отчет должен быть оставлен в соответствии с правилами и методическими указаниями к выполнению лабораторных работ и составлению отчетов.

Таблица наблюдений и вычислений.

Напряжение на зажимах	Режим работы	Наблюдаются					Вычисляются
	Холостой ход				знак φ
	Короткое замыкание				знак φ
	Короткое замыкание				знак φ

ЛИТЕРАТУРА:

Л.А. Бессонов – Теоретические основы электротехники, 1973 г. Стр. 157 – 165.

КАФЕДРА ТЕОРЕТИЧЕСКОЙ ЭЛЕКТРОТЕХНИКИ И ЭЛЕКТРИЧЕСКИХ МАШИН

ЛАБОРАТОРИЯ ТЕОРЕТИЧЕСКОЙ ЭЛЕКТРОТЕХНИКИ

РУКОВОДСТВО к лабораторной работе № 111 «ИССЛЕДОВАНИЕ РАБОТЫ ПАССИВНОГО ЧЕТЫРЕХПОЛЮСНИКА НА АКТИВНУЮ И ЕМКОСТНУЮ НАГРУЗКУ»

Программа работы.

1. Определение величин, необходимых для построения круговых диаграмм для активной и емкостной нагрузок.

2. Построение круговых диаграмм.

3. Опытная проверка построенных круговых диаграмм.

Цель работы.

Целью работы является построение круговых диаграмм для активной и емкостной нагрузок с последующей их опытной проверкой.

Основные теоретические положения.

Аналитически величины токов входного контура 1 и выходного контура 1 четырехполюсник при изменяющемся по модулю сопротивлении нагрузки могут быть определены из уравнений:

,

,

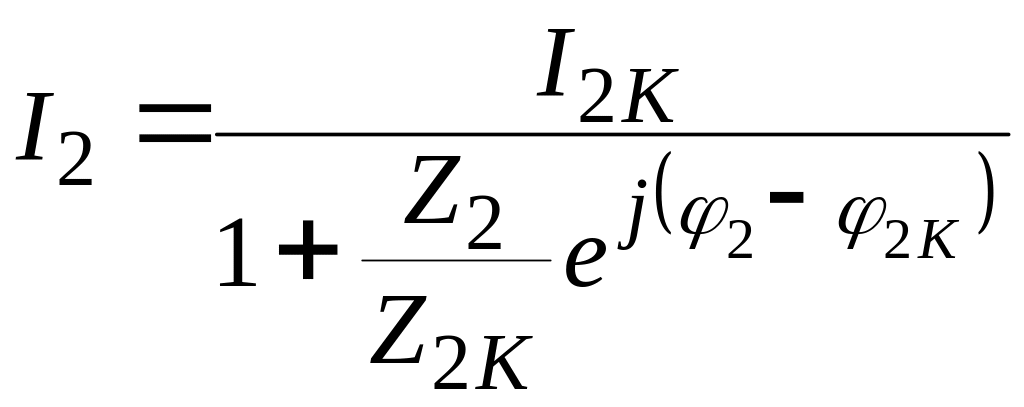которые являются векторными уравнениями окружности.

Построение круговой диаграммы выполняется в следующей последовательности:

1. Выбирается масштаб напряжения М_u1 и в этом масштабе откладывается вектор напряжения U₁ (рис.2).

2. Выбирается масштаб тока М_i1 и в этом масштабе откладываются векторы токов (отрезок ) и 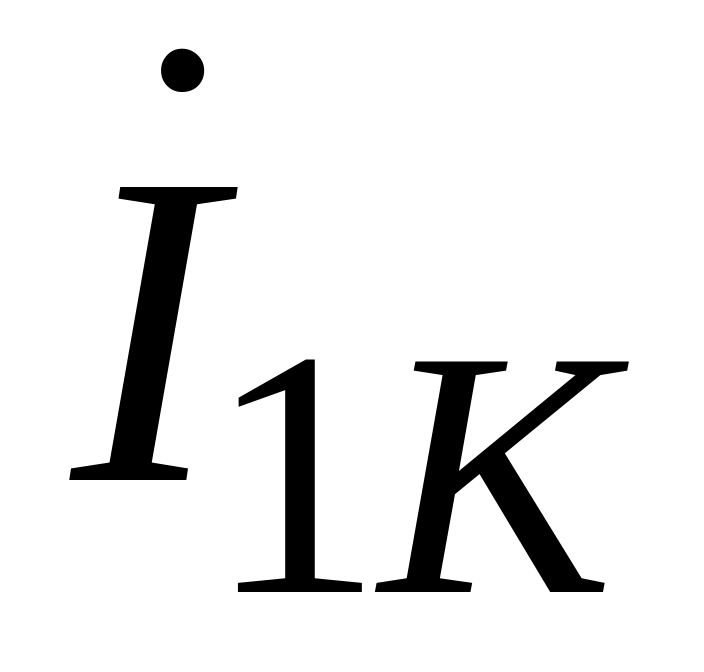(отрезок ) соответственно под углами и .

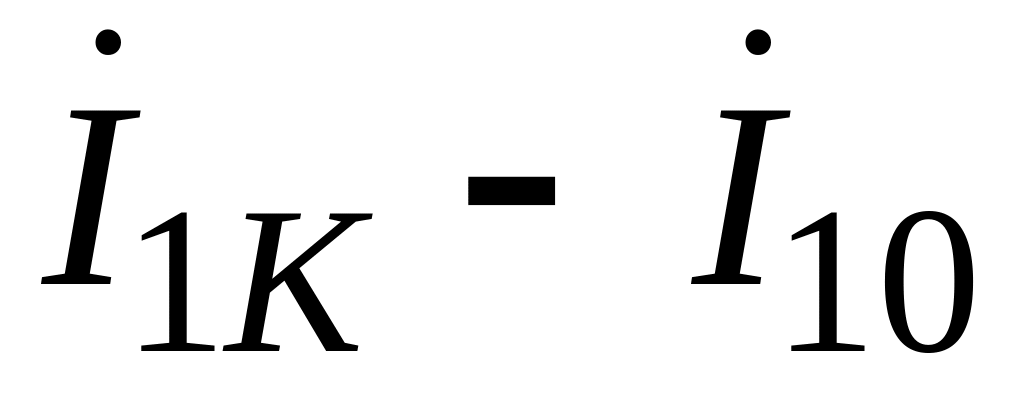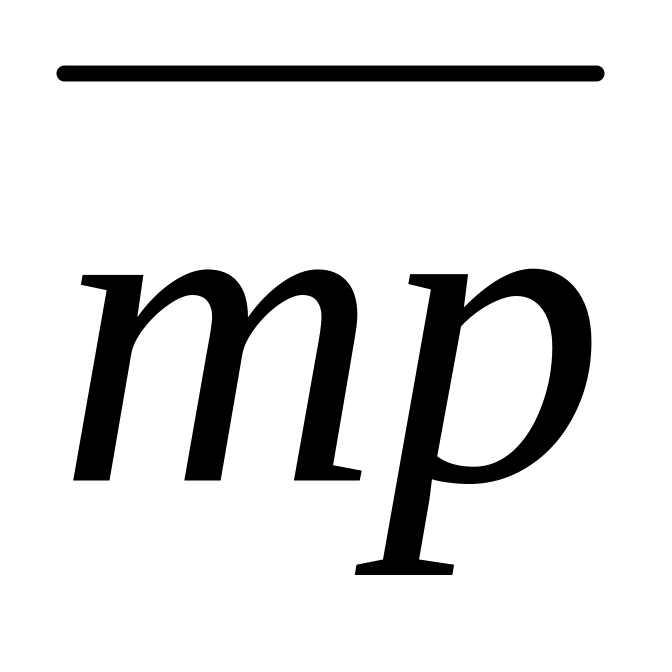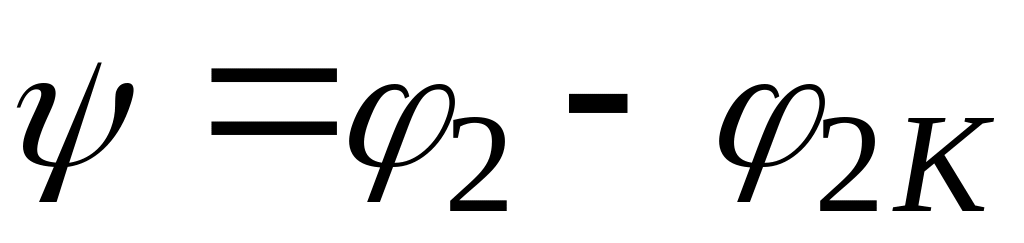3. Проводится хорда (отрезок ) и под углом к продолжению хорды проводится касательная к окружности (отрезок ). Центр окружности находится как пересечение перпендикуляра, проведенного через середину хорды и перпендикуляра к касательной из конца хорды.

4. Выбирается масштаб сопротивлений M_Z и вдоль хорды откладывается величина Z_2К (отрезок ).

5. Под углом 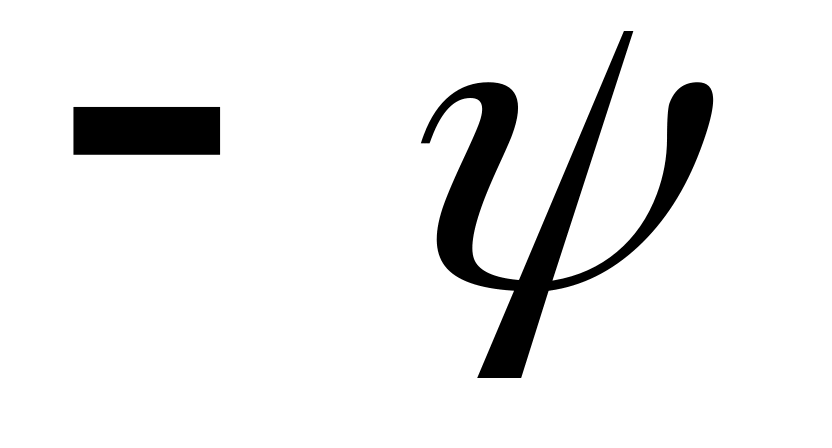к продолжению хорды проводится линия qS – линия модуля переменного сопротивления Z₂.

Дуга окружности mnp является геометрическим местом концов векторов тока при изменении Z₂.

Для любого значения Z₂ можно отложить отрезок 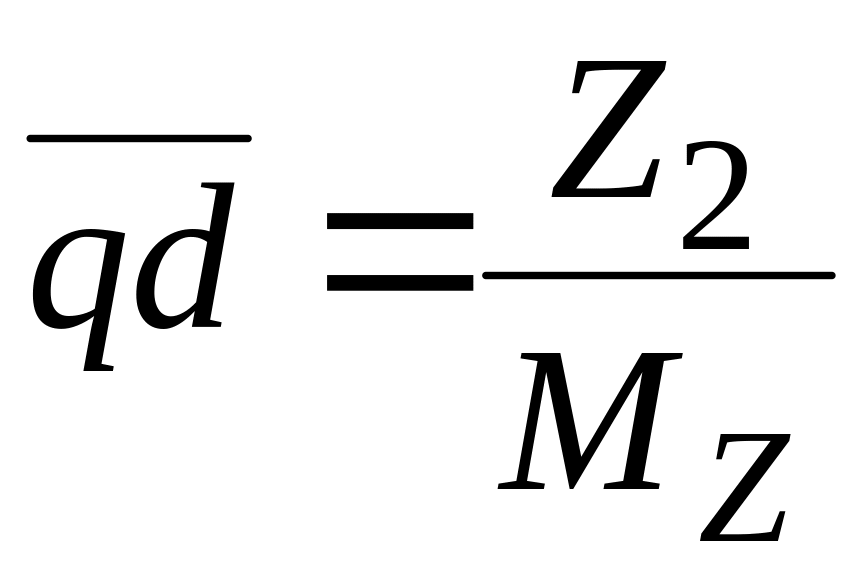и на пересечении линии md с окружностью в точке n найти положение конца вектора тока (отрезок ). Из этой же диаграммы могут быть определены также модуль тока (отрезок ), модуль напряжения на нагрузке (отрезок ), активная P₁ (отрезок ) и реактивная Q1 (отрезок ) мощности, причем масштабы U₂, I₂, P₁ и Q₁ определяются следующими выражениями:

;

;

.

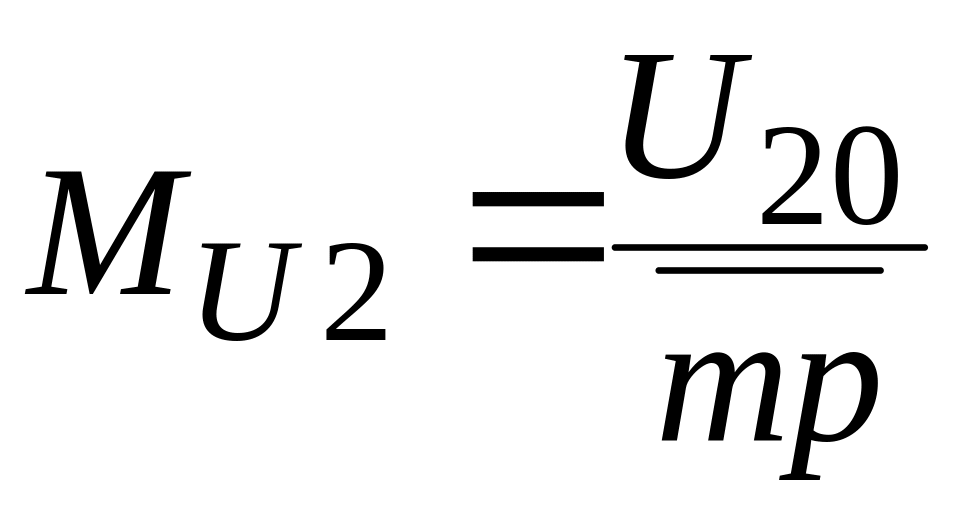Практические указания к выполнению работы.

1. Собрать схему рис.1. Величина напряжения U₁ на входных зажимах четырехполюсника выбирается по указанию преподавателя, но так, чтобы ток I_2К не превышал 3А.

2. При неизменном напряжении U₁ измерить ток холостого хода I₁₀ и ток короткого замыкания I_1К. записать комплексы этих токов, используя для этой цели данные предыдущей работы:

;

.

3. Построить на одном чертеже круговые диаграммы четырехполюсника для активной и реактивной нагрузок и подсчитать масштабы M_u2, M_i2 и M_P1.

4. На выход четырехполюсника (зажимы 2-2) включить активную или реактивную нагрузку и поддерживая напряжение U₁ неизменным записать значения измеряемых величин для 4–5 различных значений нагрузок. Полученные данные нанести на круговую диаграмму.

5. С помощью уравнений четырехполюсника подсчитать величины тока и напряжения на входе для нагрузки Z₂ (по указанию преподавателя) и сравнить их с опытными данными.

6. Отчет составляется в соответствии с требованиями правил и методических указаний к выполнению лабораторных работ и составлению отчетов.

7. Таблица результатов измерений, расчетов и данных, полученных из круговой диаграммы.

№№ п.п.

Измерения

Расчет

Данные из круговой диаграммы

В

А

Вт

В

А

Ом

Вт

А

Вт

ВАр

А

В

ЛИТЕРАТУРА:

Л.А. Бессонов – Теоретические основы электротехники, 1973 г. Стр. 167, 171 – 173.

КАФЕДРА ТЕОРЕТИЧЕСКОЙ ЭЛЕКТРОТЕХНИКИ И ЭЛЕКТРИЧЕСКИХ МАШИН

ЛАБОРАТОРИЯ ТЕОРЕТИЧЕСКОЙ ЭЛЕКТРОТЕХНИКИ

РУКОВОДСТВО к лабораторной работе № 112 «ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЦЕПИ ПРИ СОЕДИНЕИИ НАГРУЗКИ ЗВЕЗДОЙ И ЗВЕЗДОЙ С НУЛЕВЫМ ПРОВОДОМ»

Программа работы.

1. Исследование трехфазной цепи при соединении приемников звездой без нулевого провода.

2. Исследование трехфазной цепи при соединении приемников звездой с нулевым проводом.

3. Расчет и построение векторных диаграмм по п.2.

4. Составление отчета.

Цель работы.

Работа имеет целью ознакомить студентов со своеобразием режимов работы трехфазных цепей, основными методами расчета этих режимов и методами измерения мощности в трехфазных цепях.

Основные теоретические положения.

1. Источником питания трехфазных приемников переменного тока является трехфазная сеть, которая может быть трехпроводной и четырехпроводной. В теоретической электротехнике эта сеть принимается за условный трехфазный генератор симметричных фазных и линейных напряжений.

При четырехпроводной трехфазной сети обмотки (фазы) условного генератора считаются соединенными в звезду с выведенной нулевой точкой (нейтралью) N. В нейтральной точке N генератора соединены “концы” фаз. К этой точке присоединяется провод, называемый нулевым. К “началам” фаз генератора присоединяются линейные провода.

При трехпроводной трехфазной цепи фазы условного генератора могут быть соединены любым способом (в звезду или треугольник).

Напряжение между нейтралью генератора и линейным проводом называется напряжением сети. Напряжение между линейными проводами называется линейным напряжением.

Фазные и линейные напряжения сети всегда (кроме аварийных режимов) образуют симметричные системы векторов (рис.1) и связаны между собой соотношением:

Фазы трехфазного приемника (нагрузки) для совместной работы могут быть соединены звездой или треугольником.

Рассмотрим работу трехфазной трехпроводной цепи при соединении нагрузки звездой. В этом случае нагрузка и сеть (условный генератор) образуют сложную электрическую цепь с двумя узлами (рис.2). по любому линейному проводу и по фазе нагрузки, присоединенной к этому линейному проводу, протекает один и тот же ток, то есть:

.

В общем случае, комплексы полных сопротивлений фаз нагрузки могут быть не равны между собой

и такая нагрузка называется несимметричной.

При несимметричной нагрузке между узловыми точками N и схемы рис.2 появляется напряжение U_N0, называемое в трехфазных цепях смещением нейтрали:

.

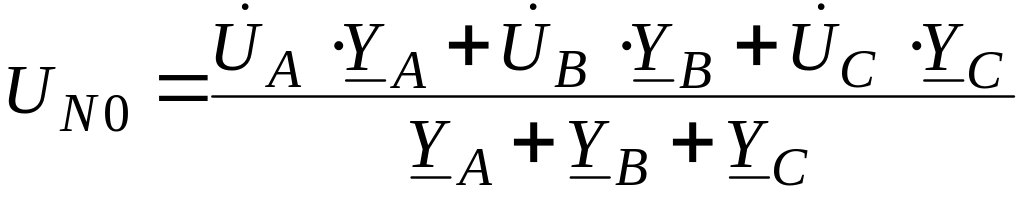Напряжения на фазах нагрузки и фазные токи:

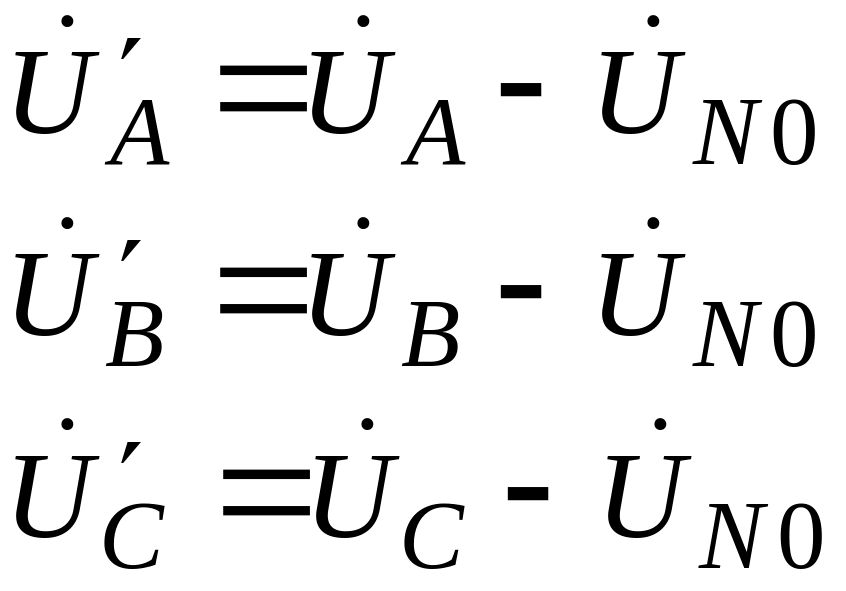
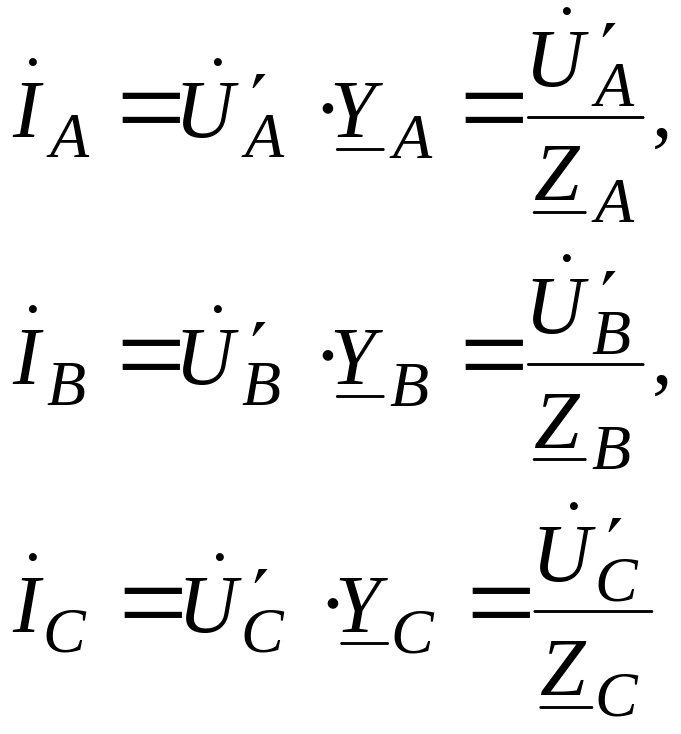
образуют несимметричные системы векторов (рис.3). чем больше асимметрия нагрузки, тем больше асимметрия токов и напряжений на фазах нагрузки.

Отсюда следует, что добиться нормальной работы трехфазного асимметричного приемника, соединенного звездой, – невозможно.

При симметричной нагрузке смещение нейтрали напряжения на фазах нагрузки равны фазным напряжениям сети и токи образуют симметричную систему векторов.

2. Мощность трехфазной цепи в общем случае равна сумме мощностей отдельных фаз:

.

Из этой формулы видно, что мощность трехфазной цепи может быть измерена тремя ваттметрами (рис.4). в этом случае, токовые обмотки ваттметров включаются последовательно в каждую фазу, а обмотки напряжения ваттметров включаются на соответствующие напряжения фаз нагрузки.

Мощность трехфазной цепи можно измерить и двумя ваттметрами, включенными по одной из трех схем, приведенных на рис.5.

Мгновенная мощность трехфазной цепи

(1).

Но, так как по 1-му закону Кирхгофа и , то:

(2).

Полученное выражение соответствует схеме включения ваттметров, показанной на рис.5в. Первое слагаемое этого выражения дает мощность некоторой фиктивной цепи, работающей на напряжении U_AB при токе I_A. Эта мощность измеряется ваттметром W₁.

Второе слагаемое дает мощность другой фиктивной цепи, работающей на напряжении U_CB при токе I_C. Эта мощность измеряется ваттметром W₂.

Таким образом, сумма показаний двух ваттметров, включенных по схеме рис.5 действительно равна активной мощности трехфазной цепи.

Заметим, что мощности, показываемые каждым из ваттметров в отдельности, физического смысла не имеют. Более того, в некоторых случаях (при и при значительной асимметрии) показания одного из ваттметров могут быть отрицательными. В этом случае мощность трехфазной цепи определяется алгебраической суммой показаний приборов.

3. Для того, чтобы обеспечить нормальную работу несимметричных трехфазных потребителей, соединенных в звезду, и однофазных потребителей, питающихся от трехфазной сети, используются трехфазные четырехпроводные сети, то есть сети с нулевым проводом. Наличие нулевого провода, обладающего малым сопротивлением ( ), приводит к тому, что потенциалы нейтральной точки генератора и нулевой точки потребителя остаются практически одинаковыми, независимо от степени ассиметрии и нагрузки.

Таким образом, в трехфазной четырехпроводной цепи (соединение “звезда – звезда с нулевым проводом”) каждая фаза нагрузки работает независимо от других и напряжения на фазах нагрузки равны фазным напряжениям сети. Векторная диаграмма напряжений всегда имеет вид, изображенный на рис.1. Векторная диаграмма токов при симметричной нагрузке имеет вид, приведенный на рис.6 (для активно-индуктивного приемника), а при несимметричной нагрузке вид рис.7.

Ток в нулевом проводе равен геометрической сумме фазных токов. При симметричной нагрузке ток в нулевом проводе равен нулю.

В трехфазной четырехпроводной цепи мощность несимметричной нагрузки можно измерить только с помощью трех ваттметров, измеряя мощность каждой фазы.

Метод двух ваттметров для четырехпроводных цепей в общем случае не применим.

Практические указания к выполнению работы.

Для исследования трехфазной трехпроводной цепи при соедини нагрузки в звезду собирается схема, изображенная на рис.8 и снимаются показания приборов для случаев:

1. симметричной нагрузки;

2. трех-четырех значений несимметричной нагрузки.

В качестве нагрузки берутся активно-емкостные двухполюсники, имеющиеся на лабораторном стенде. Два из трех активно-емкостных двухполюсников – регулируемые (емкость, присоединенная параллельно или последовательно с активным сопротивлением, изменяется ступенями через 10 мкФ от 0 до 70 мкФ).

Перед сборкой схемы рис.8 необходимо определить параметры нерегулируемого двухполюсника, что необходимо в дальнейшем при вычислении активной мощности нерегулируемой фазы.

Для каждого опыта мощность цепи следует определять двумя методами:

1. с помощью двух ваттметров (переключатель П замкнут в положение 2);

2. измерением мощности пофазно, при этом мощность регулируемых фаз нагрузки измеряется ваттметрами (переключатель П замкнут в положение 1), а мощность нерегулируемой фазы определяется расчетом.

Мощность цепи, полученная двумя методами, для каждого опыта должна быть одинаковой.

Результаты измерений и вычислений сводятся в таблицу. На основании полученных результатов делаются выводы о режимах работы рассматриваемой цепи и методах измерения мощности.

2. Для выполнения п.2 собирается схема рис.9, отличающиеся от схемы рис.8 лишь тем, что нейтральная точка нагрузки соединена через амперметр с нейтральной точкой сети.

Показания приборов снимаются для случаев:

1. одинаковой (симметричной) нагрузки фаз;

2. отсутствия нагрузки в какой-нибудь фазе (обрыв фазы);

3. трех-четырех промежуточных значений сопротивлений регулируемых фаз.

Результаты измерений заносятся в таблицу.

По данным таблицы вычисляются углы сдвига фаз между напряжениями и токами и строятся векторные диаграммы напряжений и токов для симметричной нагрузки, обрыва фазы и одного из промежуточных значений (по указанию преподавателя). Векторная диаграмма при обрыве фазы B активно-индуктивного приемника и при имеет вид, изображенный на рис.10.

Мощность цепи находят, как и в предыдущем случае, двумя методами. Результаты измерений двумя методами будут равные, так как метод двух ваттметров при наличии нулевого провода дает неверные результаты. На это следует указать в отчете.

3. Отчет должен быть составлен в соответствии с правилами и методическими указаниями к выполнению лабораторных работ и составлению отчетов.

4. Таблица результатов измерений параметров нерегулируемой фазы аналогична таблице в лабораторной работе № 105.

5. Таблица результатов измерений и расчетов при соединении нагрузки звездой без нулевого провода.

   №№ п.п.

   Измерения

   Расчет

   Двумя ваттметрами

   Пофазно

   В

   В

   В

   А

   А

   А

   Вт

   Вт

   Вт

   Вт

   Вт

   Вт

   Вт

6. В таблицу измерений и расчетов при соединении нагрузки звездой с нулевым проводом в графы “измерения” добавить колонку для записи значений тока в нулевом проводе.

ЛИТЕРАТУРА:

Л.А. Бессонов – Теоретические основы электротехники, 1973 г. Стр. 180 – 181, 183 – 185.