Кафедра теоретической электротехники и электрических машин лаборатория теоретической электротехники Руководство к лабораторной работе № 102 «исследование разветвленной цепи постоянного тока»

Программа работа.

1. Экспериментальная проверка законов Кирхгофа.

2. Экспериментальная проверка метода наложения.

Цель работы.

Работа имеет своей целью произвести экспериментальную проверку законов Кирхгофа и метода наложения на примере цепей постоянного тока.

Основные теоретические положения.

1. Движение зарядов в электрической цепи так, что ни в одном из узлов цепи заряды не скапливаются. Из физической сущности этого процесса вытекает первый закон Кирхгофа: сумма токов, притекающих к узлу разветвления равна сумме токов, утекающих от узла. Для узла, изображенного на рис. 1, согласно формулировке имеем:

Если условно принять токи, подтекающие к узлу, положительными, а токи, утекающие от узла – отрицательными, то можно записать:

или

Последнее выражение также является математической записью первого закона Кирхгофа в следующей формулировке: алгебраическая сумма токов, подтекающих к любому узлу схемы равна нулю.

В любом замкнутом контуре электрической цепи соотношение между ЭДС, действующими в контуре, и напряжениями на отдельных его участках определяется вторым законом Кирхгофа: алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме напряжений на отдельных участках этого контура, т.е.

В каждую из этих сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура и со знаком минус – если они не совпадают с ним.

Например, для контура “abca” схемы, изображенной на рис. 2 по второму закону Кирхгофа имеем:

2. Ток в любой ветви сколько угодно сложной электрической цепи, составленной из линейных элементов, можно рассматривать как алгебраическую сумму частичных токов, создаваемых в этой ветви каждым источником ЭДС, действующим отдельно от других. Это положение в электротехнике называется принципом наложения или суперпозиции. Этот принцип положен в основу одного из методов расчета сложных электрических цепей, получившего название метода наложения

Метод наложения позволяет расчленять сложную электрическую цепь со многими источниками ЭДС на ряд более простых в расчетном отношении цепей, в каждой из которых действует только одна ЭДС, а все другие источники ЭДС предполагаются замкнутыми накоротко. Внутренние сопротивления источников (если ими нельзя пренебречь) должны быть включены в соответствующие ветви.

Применяя метод наложения для расчета цепи, изображенной на рис. 3, получим две более простые цепи (рис. 4 и рис. 5).

Частичные токи в ветвях схемы рис. 4:

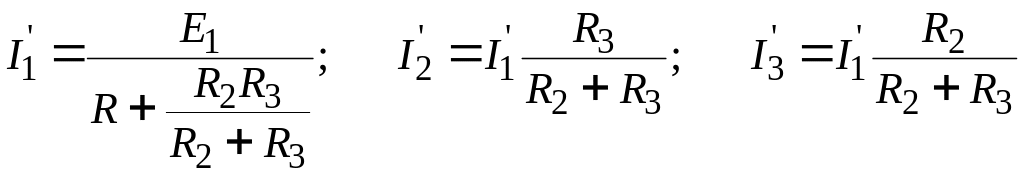
Частичные токи в ветвях схемы рис. 5:

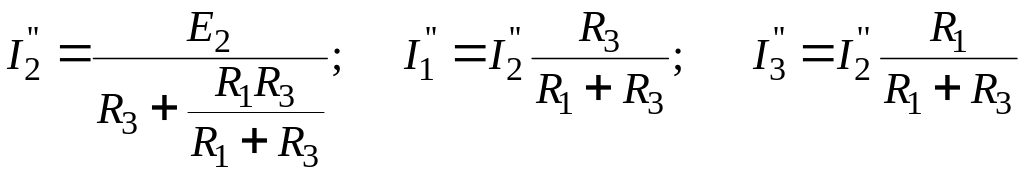
Произведя наложение частичных токов, получим:

Практические указания к выполнению работы.

1. Для выполнения экспериментальной проверки первого закона Кирхгофа собрать схему, изображенную на рис. 6.

При двух различных значениях сопротивлений произвести замер токов. По закону Ома вычислить сопротивления ветвей и эквивалентное сопротивление всей цепи. Результаты измерений и вычислений внести в таблицу 1.

Таблица 1.

№№	Результаты измерений					Вычисления
	В	А	А	А	А	Ом	Ом	Ом	Ом
1-й опыт
2-й опыт

По результатам измерений проверяется справедливость первого закона Кирхгофа.

2. Для экспериментальной проверки второго закона Кирхгофа и метода наложения собрать схему, изображенную на рис. 6.

В качестве источников ЭДС используются сеть постоянного тока и аккумуляторная батарея. ЭДС источников замеряются при разомкнутых рубильниках и . Замеры токов в ветвях схемы произвести для трех случаев:

а) рубильник замкнут в положение 2, а рубильник – в положение 1;

б) рубильник замкнут в положение 1, а рубильник – в положение 2;

в) рубильники и замкнуты в положениях 2 и 2.

Результаты измерений и расчетов токов методом наложения занести в таблицу 2.

№№ опытов
	В	В	А	А	А	А	А	А	А	А	А
1-й опыт
2-й опыт
3-й опыт
наложение

Сравнить результаты непосредственного измерения токов , и (3-й опыт) с результатами, полученными наложением частичных токов.

Для каждого из опытов составить уравнения по второму закону Кирхгофа и подставив значения токов, полученных в соответствующем опыте, проверить правильность составленных уравнений.

Сопротивления , и определить по закону Ома. Для этого в одном из опытов необходимо измерить напряжения на этих сопротивлениях.

ЛИТЕРАТУРА

Л. А. БЕССОНОВ – Теоретические основы электротехники, 1972 г. Стр. 20, 21, 41, 42, 43.

КАФЕДРА ТЕОРЕТИЧЕСКОЙ ЭЛЕКТРОТЕХНИКИ И ЭЛЕКТРИЧЕСКИХ МАШИН

ЛАБОРАТОРИЯ ТЕОРЕТИЧЕСКОЙ ЭЛЕКТРОТЕХНИКИ

Руководство к лабораторной работе № 103 «ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЛИНЕЙНЫХ СООТНОШЕНИЙ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ. ПЕРЕДАЧА ЭНЕРГИИ ОТ ДВУХПОЛЮСНИКА К НАГРУЗКЕ»

Программа работы.

1. Проверить линейные зависимости между изменениями токов и напряжений на отдельных участках сложной электрической цепи.

2. Экспериментально проверить расчет сложной цепи методом эквивалентного генератора.

Цель работы.

Работа имеет целью показать студентам экспериментально, что в линейных электрических цепях токи и напряжения в своих изменениях связаны линейными соотношениями, а также экспериментально проверить расчет цепи методом эквивалентного генератора.

Основные теоретические положения.

1. Если в электрической цепи, составленной из линейных элементов, изменяется ЭДС или сопротивление какой-либо ветви, то две любые величины (токи или напряжения) двух других любых ветвей связаны между собой в своих изменениях линейными зависимостями вида

где x – ток или напряжение одной ветви, а y – ток или напряжение другой ветви.

Например, при изменении ЭДС в ветви “к” (или сопротивления этой ветви ) ток в ветви “p” и ток в ветви “б” будут связаны соотношением

где – коэффициент, имеющий размерность тока

– безразмерный коэффициент.

Аналогичным соотношением связаны и напряжения различных ветвей.

Коэффициенты и могут быть определены как расчетным, так и экспериментальным путем. При экспериментальном определении коэффициентов и достаточно определить значения двух токов (напряжений) в двух различных ветвях при двух различных режимах работы схемы.

Если в первом опыте , а и во втором опыте , а , то можно записать:

.

Решив эту систему уравнений с двумя неизвестными относительно и , получим:

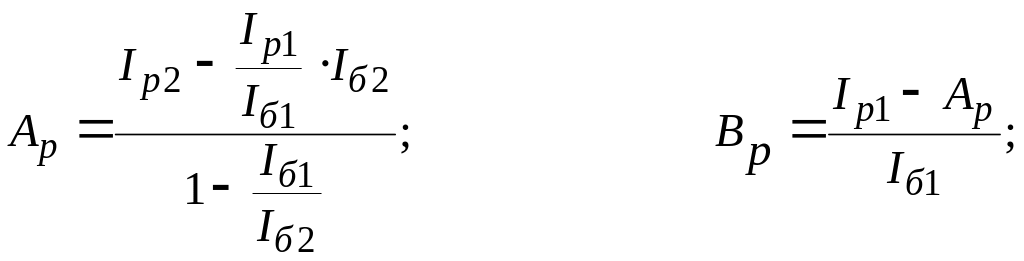
2. В электрической схеме любой сложности всегда можно выделить любую одну ветвь и тогда остальная часть схемы по отношению к выделенной ветви будет являться двухполюсником (поскольку она присоединяется к выделенной ветви двумя зажимами или полюсами). При наличии в двухполюснике источников энергии, двухполюсник называется активным, а при отсутствии источников – пассивным (см. рис. 1).

В расчетном отношении активный двухполюсник можно заменить эквивалентным генератором. ЭДС этого генератора равна напряжению холостого хода на зажимах двухполюсника, а внутреннее сопротивление эквивалентного генератора равно входному сопротивлению двухполюсника.

Для того, чтобы доказать возможность такой замены включим в ветвь “аb” (рис. 1б) две одинаковые по величине, но противоположные по направлению ЭДС и . Очевидно, что ток в выделенной ветви “ab” от этого не изменится.

В соответствии с принципом наложения ток в ветви можно рассматривать как сумму частичных токов, т.е.

(1)

где – частичный ток, создаваемый в ветви “ab” действием ЭДС и всеми ЭДС, имеющимися в двухполюснике (рис. 1в);

– частичный ток, создаваемый в ветви “ab” действием только ЭДС (рис. 1г).

ЭДС направлена встречно , поэтому

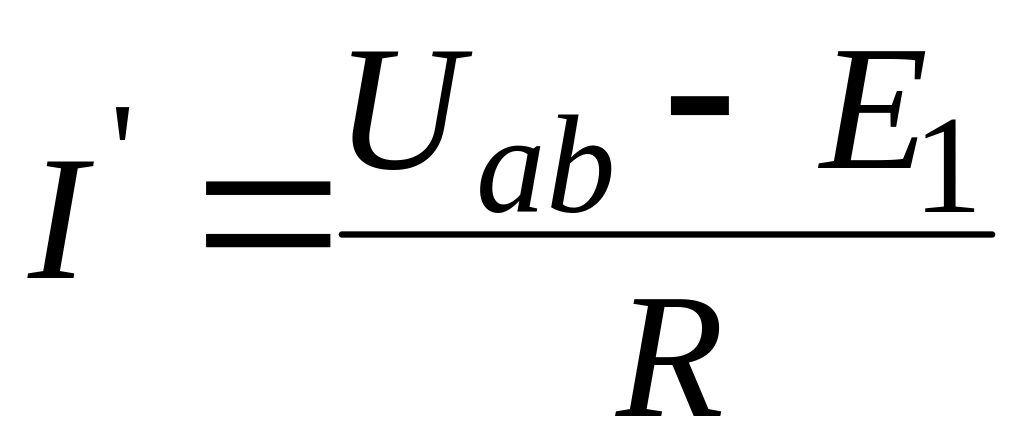(2)

можно выбрать так, что ток ветви “ab” будет равен нулю, т.е. . Отсутствие тока в ветви равносильно ее размыканию, т.е. холостому ходу двухполюсника.

Таким образом, если взять , то , но в соответствии с рис. 1г

(3),

Где – входное сопротивление по отношению к зажимам “ав”,

– сопротивление ветви “аb”.

Уравнению (3) соответствует эквивалентная схема, приведенная на рис. 2. Схему эту можно рассматривать как эквивалентный генератор. Последовательность расчета цепи методом эквивалентного генератора:

1. Найти 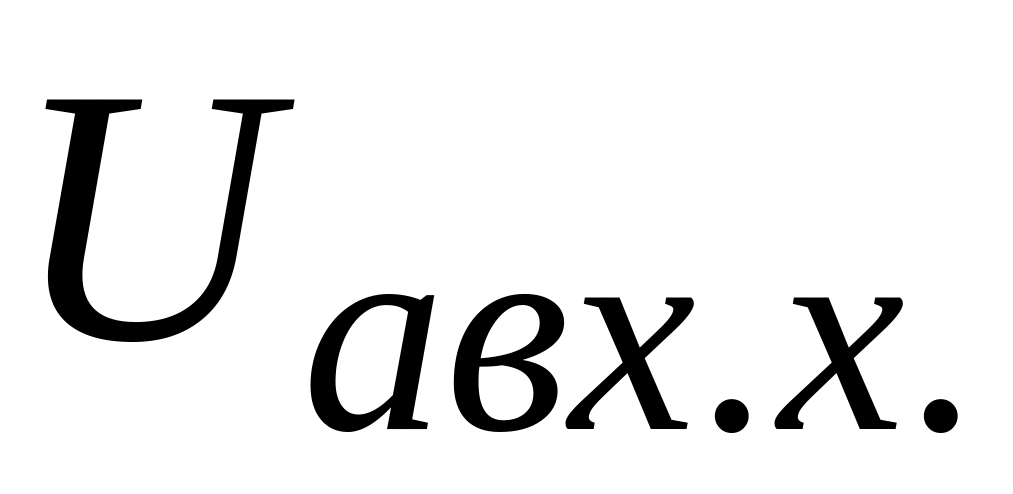на зажимах разомкнутой ветви. Для этого необходимо рассчитать токи в схеме при разомкнутой ветви и определить .

2. Определить входное сопротивление всей схемы по отношению к зажимам “аb” (все источники энергии закорочены, а их внутренние сопротивления оставлены).

3. Подсчитать ток в рассматриваемой ветви по формуле (3). Если сделать , то в схеме будет режим короткого замыкания

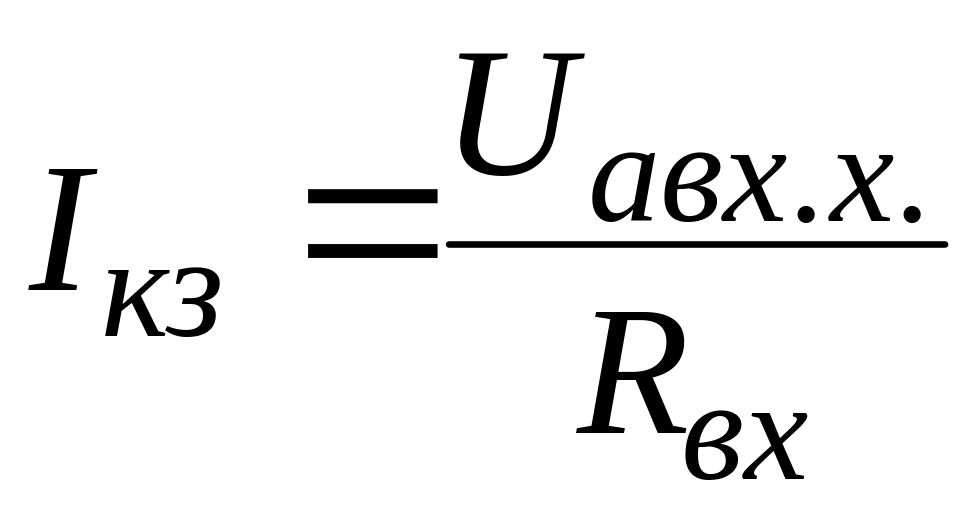откуда (4).

Из формулы (4) вытекает простой способ экспериментального определения входного сопротивления двухполюсника: измерить напряжение , ток короткого замыкания и взять их отношение.

Практические указания к выполнению работы.

1. Собрать схему, изображенную на рис. 3 и произвести опыт холостого хода (рубильник P разомкнут) и опыт короткого замыкания (рубильник P замкнут) при . Результаты опытов записать в таблицу 1.

2. По данным таблицы 1 определить коэффициенты , , , и построить аналитические зависимости

(5)

(6).

3. Определить величины сопротивлений, включенных в схему.

Таблица 1

Опыты	Опытные данные				Расчетные величины
Опыт	В	В	А	А	–	–	–	–
Опыт х.х.
Опыт к.з.

Результаты замеров и вычислений по п. 3 заносятся в таблицу 2.

Таблица 2.

По данным таблицы 2 рассчитать входное сопротивление схемы относительно зажимов “а” и “b”.

4. Изменяя сопротивление от 0 до , произвести 7–8 замеров величин и результаты замеров внести в таблицу 3.

Таблица 3.

№№ опытов		Опытные данные				Расчетные данные
	В	В	А	А	А	Вт	Вт	Вт	–

По данным таблицы 3:

а) построить в одной системе координат зависимости:

В этой же системе координат построить прямую по уравнению (5).

б) построить в одной системе координат зависимость

и в этой же системе координат построить прямую по уравнению (6).

5. Установить величину по указанию преподавателя и, уменьшая напряжение на зажимах цепи до нуля, записать показания приборов для 7–8 точек в таблицу 4.

По данным таблицы 4 построить зависимости:

Таблица 4.

№№ п.п.		Опытные данные				Расчетная величина
	В	В	А	А	А	Вт

6. Методом эквивалентного генератора рассчитать токи при значениях сопротивления , взятых из таблицы 3 и сравнить результаты расчетов с данными таблицы 3.

ЛИТЕРАТУРА

Л. А. БЕССОНОВ – Теоретические основы электротехники, 1973 г. Стр. 26–27, 38–42.