2.3 Методика выполнения расчётов

Задание: определить показатели работоспособности шатунных подшипников двигателя КамАЗ – 740. Критерием предельного состояния шатунного подшипника является зазор. Величина зазора определяется суммарным износом деталей подшипника – шейки коленчатого вала, верхнего и нижнего вкладышей. Пример исходных данных задания приведён в таблице 6, в которой даны парные значения пробега автомобилей и износа деталей.

Расчёты начинают с обоснования моделей потери работоспособности отдельными деталями шатунного подшипника. Поле корреляции величины износа деталей и наработки показаны на рисунке 3 .

Из графиков следует, что зависимости величины износа от наработки не линейны и включают зону повышенной интенсивности изнашивания в период приработки.

Для практических целей важным является зона, в которой величины износа приближаются к допустимым значениям. Поэтому, чтобы не усложнять функцию модели, зону приработки можно исключить из анализа. Для этого нужно определить величину износа к моменту окончания приработки.

Таблица 6 – Износ деталей шатунного подшипника двигателя КамАЗ – 740

Пробег, тыс. км.	Износ деталей, мкм.				Пробег, тыс. км.	Износ деталей, мкм.
	Шейка вала	Вкладыш верхний	Вкладыш нижний			Шейка вала	Вкладыш верхний	Вкладыш нижний
158	19	45	28		90	15	29	20
234	46	113	77		212	35	101	73
102	14	33	20		264	57	98	64
2	3	6	4		237	43	123	63
127	19	41	25		14	9	22	15
58	12	26	17		121	15	33	24
219	48	79	63		35	12	24	16
88	13	30	18		220	44	85	51
174	30	60	45		26	10	24	16
19	11	23	15		114	18	33	22
20	10	24	15		8	8	18	12
195	44	81	43		206	50	61	45
100	14	33	19		158	22	49	33
221	33	107	68		142	23	46	24
49	12	26	17		6	7	16	11
219	54	94	78		243	42	98	79
146	23	43	29		147	19	40	28
280	56	124	76		69	13	28	18
22	10	24	15		245	54	104	55
249	49	126	72		16	10	23	15
116	17	35	22		204	46	72	61
278	54	107	71		203	37	81	51
228	53	105	58		245	57	110	74
4	6	12	8		62	12	27	17
10	9	21	14		173	23	55	38
245	51	77	68		190	22	52	55
108	17	31	21		71	13	27	18
193	25	66	37		12	9	22	15
132	22	43	25		82	15	30	19
60	12	26	17		73	12	28	17
88	14	30	19		61	13	27	17
147	17	38	28		260	53	114	72
180	23	73	42		12	10	23	15
218	41	112	55		168	24	45	35
208	30	87	67		282	60	116	78
230	38	72	74		167	20	61	28
206	39	87	58		241	59	89	70
222	40	120	49		141	17	36	27
184	36	72	51		51	13	26	17
223	56	64	71		172	21	53	34
189	31	52	45		255	47	87	59
78	13	29	18		164	27	58	35

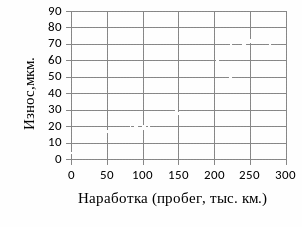
Рисунок 3 – Поле корреляции величины износа деталей шатунного подшипника и наработки двигателя КамАЗ – 740: a – шейки коленчатого вала, b – верхнего шатунного вкладыша, c – нижнего шатунного вкладыша

С этой целью на графике нужно выделить участок наработки от момента окончания приработки до момента, когда зависимость износа от наработки начинает отклоняться от линейной. Как следует из рисунка 3, для всех деталей (поскольку это детали одного узла) это зона наработки от 20 до 100 тысяч километров пробега.

Таблица 7 – Выборка исходных данных для определения величины приработки

Пробег, тыс. км.	Износ деталей, мкм.				Пробег, тыс. км.	Износ деталей, мкм.
	Шейка вала.	Вкладыш верхний	Вкладыш нижний			Шейка вала.	Вкладыш верхний	Вкладыш нижний
20	10	24	15		69	13	28	18
22	10	24	15		71	13	27	18
26	10	24	16		73	12	28	17
35	12	24	16		78	13	29	18
49	12	26	17		82	15	30	19
51	13	26	17		88	14	30	19
58	12	26	17		88	13	30	18
60	12	26	17		90	15	29	20
61	13	27	17		100	14	33	19
62	12	27	17

Для формирования выборки исходных данных для определения величины приработки нужно провести сортировку таблицы исходных данных по возрастанию наработки и выбрать данные только в диапазоне от 20 до 100 тысяч километров пробега. Выборка исходных данных приведена в таблице 7.

После этого определяют величину износа за период приработки (от нуля до20000 километров пробега автомобиля) по формулам (6) и (7).

Например, для шейки коленчатого вала

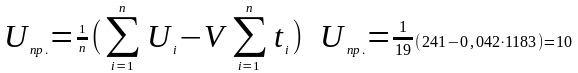
Результаты аналогичных расчётов для других деталей приведены в таблице 8.

Таблица 8 –Величина износа деталей за период приработки

Деталь	Модель начала установившегося изнашивания	Износ за период приработки, мкм
Шейка вала	0,0425t + 10,04	10
Вкладыш верхний	0,0995t + 22,067	22
Вкладыш нижний	0,0525t + 14,097	14

Графическая интерпретация определения величины приработочного износа показана на рисунке 4.

Рисунок 4 – Зависимость износа деталей шатунного подшипника в период приработки и начала установившегося изнашивания a – шейки вала, b – верхнего вкладыша, c – нижнего вкладыша

При этом следует иметь в виду, что на графике для наглядности показаны экспериментальные точки в диапазоне наработки от нуля до 100 тысяч километров, а линейная аппроксимация выполнялась по экспериментальным точкам в диапазоне от 20 до 100 тысяч километров.

Таблица 9 – Нормированные исходные данные

Пробег, тыс. км.	Износ деталей, мкм.						Пробег, тыс. км.		Износ деталей, мкм.
	Шейка вала.	Вкладыш верхний	Вкладыш нижний	Шейка вала.					Вкладыш верхний	Вкладыш нижний
22	0,01	3	1	174			20		39	31
26	0,01	3	2	180			13		52	28
35	2	3	2	184			26		51	37
49	2	5	3	189			21		31	31
51	3	5	3	190			12		31	41
58	2	5	3	193			15		45	23
60	2	5	3	195			34		60	29
61	3	6	3	203			27		60	37
62	2	6	3	204			36		51	47
69	3	7	4	206			29		66	44
71	3	6	4	206			40		40	31
73	2	7	3	208			20		66	53
78	3	8	4	212			25		80	59
82	5	9	5	218			31		91	41
88	3	9	4	219			38		58	49
88	4	9	5	219			44		73	64
90	5	8	6	220			34		64	37
100	4	12	5	221			23		86	54
102	4	12	6	222			30		99	35
108	7	10	7	223			46		43	57
114	8	12	8	228			43		84	44
116	7	14	8	230			28		51	60
121	5	12	10	234			36		92	63
127	9	20	11	237			33		102	49
132	12	22	11	241			49		68	56
141	7	15	13	243			32		77	65
142	13	25	10	245			41		56	54
146	13	22	15	245			44		83	41
147	7	17	14	245			47		89	60
147	9	19	14	249			39		105	58
158	9	24	14	255			37		66	45
158	12	28	19	260			43		93	58
164	17	37	21	264			47		77	50
167	10	40	14	278			44		86	57
168	14	24	21	280			46		103	62
172	11	32	20	282			50		95	64
173	13	34	24

После определения величины износа деталей за период приработки формируют таблицу скорректированных данных для оценки параметров моделей. Для этого из массива исходных данных (таблица 6) исключают экспериментальные точки менее величины приработки и данные приводят к нормированному виду. Массив нормированных данных приведён в таблице 9.

Далее производится выбор предполагаемых регрессионных моделей По общему виду точечных графиков можно сделать вывод о наличии нелинейности в регрессионной зависимости, а в качестве моделей можно использовать экспоненциальную, показательную и степенную функции (формулы (2), (3) и (4)).

Расчёт параметров моделей производится по формулам (8) … (13) . Для удобства расчётов необходимо сформировать таблицу EXCEL следующего вида (таблица 10).

Таблица 10 – Промежуточные данные для расчёта параметров моделей шейки коленчатого вала

t	U	ln t	ln Y	t2	ln t2	t lnU	ln t* ln U	lnU/lnt
12	0,01	2,47	-4,61	139	6,09	-54,32	-11,36	-1,87
16	0,01	2,77	-4,61	256	7,69	-73,68	-12,77	-1,66
…	…	…	…	…	…	…	…	…
35	1	3,56	0,01	1225	12,64	0,35	0,04	0,00
…	…	…	…	…	…	…	…	…
278	44	5,63	3,78	77284	31,67	1052,00	21,30	0,67
280	46	5,63	3,83	78400	31,75	1072,02	21,57	0,68
1995,1	1387,6	367,6	154,3	2329079,6	1837,6	34291,8	854,9	0,35

Определяют параметры для экспоненциальной функции.

Для показательной функции.

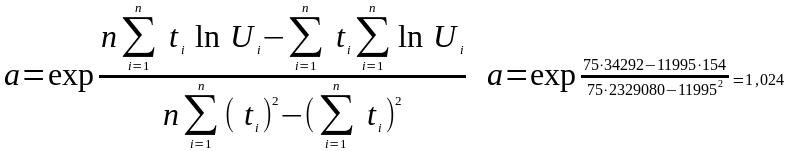
Для степенной функции.

Регрессионные модели для процесса износа шейки вала будут иметь следующий вид.

экспоненциальная

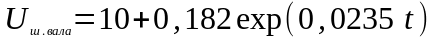
показательная

степенная

Регрессионные модели можно определить с помощью опции линия тренда на графике корреляционного поля. Эти уравнения имеют вид (без учёта приработочного износа).

= 0,185e^0,0234x = 1E-05x^2,7761

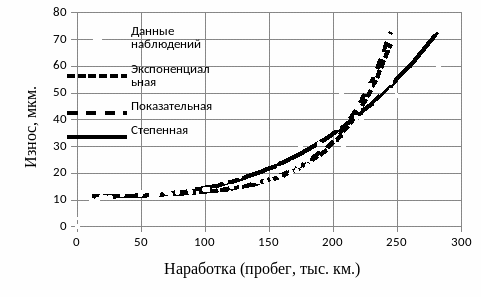
Рисунок 5 – Регрессионные модели изнашивания шатунной шейки коленчатого вала

Адекватность полученных регрессионных моделей проверяют на основе дисперсионного анализа. Анализ дисперсий изнашивания шейки коленчатого вала для различных моделей приведён в таблице 11.

Таблица 11 –Анализ дисперсий моделей изнашивания шейки коленчатого вала

Компоненты дисперсии	Сумма квадратов для моделей			Число степеней свободы		Дисперсия на одну степень свободы для моделей
	экпоненци альная	показательная	степен ная			экпоненциальная	показательная	степенная
Общая	12810	12810	12810		64		200	200	200
Факторная	15013	15910	11110		2		7507	7955	5555
Остаточная	2538	2550	1715		62		41	41	28

Фактическое значение F-критерия определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы, по формуле (55).

Критическое значение F-критерия определяется по таблицам F – распределения при данных степенях свободы и заданном уровне значимости. Для 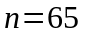, 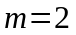и уровня значимости 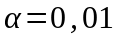(ошибка не принять нулевую гипотезу один процент) .

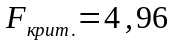Как следует из расчётов, фактическое  значение  F-критерия  значительно больше  критического для всех моделей, следовательно, признается  статистическая  значимость всех уравнений в целом.

Выбор наиболее подходящей модели из всех статистически значимых производится с помощью коэффициента детерминации (57) и относительной ошибки (16).

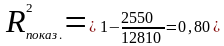
Таблица 12 – Критерии адекватности моделей изнашивания шейки коленчатого вала

Критерии	Регрессионные модели
	экспоненциальная	показательная	степенная
F-критерий расчётный	186	196	204
F-критерий критический для	4,90	4,90	4,90
Коэффициент детерминации	0,80	0,79	0,86
Относительная ошибка	0,169	0,167	0,133

Как следует из таблицы 12, наиболее подходящей моделью является степенная функция. Этот вывод можно сделать из графика 5. Подходящими моделями являются также экспоненциальная и степенная. Однако наибольший коэффициент детерминации и минимальная ошибка соответствуют степенной модели.

Регрессионные модели для верхнего вкладыша, определённые аналогичными расчётами имеют следующий вид.

Дисперсионный анализ и критерии адекватности для моделей изнашивания верхнего вкладыша шатунного подшипника приведены в таблице 13 в таблице 14.

Таблица 13–Анализ дисперсий моделей изнашивания верхнего вкладыша шатунного подшипника

Компоненты дисперсии	Сумма квадратов для моделей			Число степеней свободы		Дисперсия на одну степень свободы для моделей
	экспоненци альная	показательная	степен ная			экспоненциальная	показательная	степенная
Общая	61150	61150	61150		64		955	955	955
Факторная	60053	69745	34845		2		30027	34873	17423
Остаточная	9279	9931	9564		62		150	160	154

Рисунок 6 – Регрессионные модели изнашивания верхнего вкладыша шатунного подшипника

Таблица 14 – Критерии адекватности моделей изнашивания верхнего вкладыша шатунного подшипника

Критерии	Регрессионные модели
	экспоненциальная	показательная	степенная
F-критерий расчётный	201	218	113
F-критерий критический для	4,90	4,90	4,90
Коэффициент детерминации	0,84	0,83	0,84
Относительная ошибка	0,102	0,096	0,100

Регрессионные модели для нижнего вкладыша имеют следующий вид.

Дисперсионный анализ и критерии адекватности для моделей изнашивания нижнего вкладыша шатунного подшипника приведены в таблицах 15 и16.

Таблица 15 –Анализ дисперсий моделей изнашивания нижнего вкладыша шатунного подшипника

Компоненты дисперсии	Сумма квадратов для моделей			Число степеней свободы		Дисперсия на одну степень свободы для моделей
	экспоненци альная	показательная	степен ная			экспоненциальная	показательная	степенная
Общая	28691	28691	28691		64		448	448	448
Факторная	31744	27128	18886		2		15872	13564	9443
Остаточная	4848	4850	3496		62		77	77	55

Таблица 16 – Критерии адекватности моделей изнашивания нижнего вкладыша шатунного подшипника

Критерий	Регрессионные модели
	экспоненциальная	показательная	степенная
F-критерий( расчётный)	206	176	170
F-критерий (критический для  )	4,90	4,90	4,90
Коэффициент детерминации	0,83	0,83	0,88
Относительная ошибка	0,099	0,107	0,083

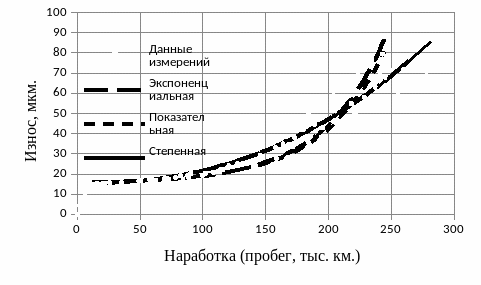
Рисунок 7 – Регрессионные модели изнашивания нижнего вкладыша шатунного подшипника

Как следует из таблиц, для верхнего вкладыша наиболее подходящей моделью приближения к отказу является показательная функция, а для нижнего вкладыша – экспоненциальная.

Так как критерием предельного состояния шатунного подшипника является зазор, модель потери работоспособности шатунного подшипника имеет вид.

По этому уравнению можно определить долговечность подшипника (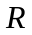 ). Для этого нужно решить это уравнение относительно наработки при известном значении величины предельного износа.

По данным нормативно-технических документов по ремонту автомобилей КамАЗ – 740 предельным значением суммарного износа деталей шатунных подшипников является износ 0,24 мм. Тогда уравнение имеет вид.

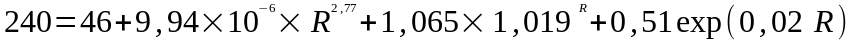
В аналитическом виде это сделать невозможно. Для решения можно использовать опцию поиск решения на вкладке данные в программе Excel. Результат решение тысяча километров пробега автомобиля.

Для определения вероятности безотказной работы необходимо знать рассеивание относительно среднестатистической модели. Для этого производится статистическая обработка всего массива данных суммарного износа деталей подшипника.

Суммарный износ шейки вала, верхнего и нижнего вкладышей шатунного подшипника, определённый суммированием износа отдельных деталей, при различных пробегах автомобиля приведён в таблице 17 .

Таблица 17 – Суммарный износ шейки вала, верхнего и нижнего вкладышей шатунного подшипника двигателя КамАЗ – 740 при различных пробегах автомобиля

Пробег, тыс. км.	Износ, мкм.	Пробег, тыс. км.	Износ, мкм.	Пробег, тыс. км.	Износ, мкм.	Пробег, тыс. км.	Износ, мкм.	Пробег, тыс. км.	Износ, мкм.
174	133	100	65	190	138	22	48	152	103
223	189	203	167	78	58	255	191	16	49
158	90	220	178	245	239	206	198	237	227
264	217	270	254	61	54	234	258	206	155
182	105	228	214	180	136	260	237	127	83
35	50	250	217	26	49	141	78	245	194
19	49	108	67	71	56	278	230	130	70
146	93	62	54	230	182	173	114	208	182
12	45	10	43	158	102	88	61	195	153
212	207	219	143	245	211	12	46	195	178
116	72	73	55	82	62	60	53	223	238
233	198	90	62	212	168	167	107	102	66
8	38	203	126	51	54	58	53	4	25
168	101	184	157	135	88	249	251	147	85
2	14	220	158	193	126	221	223	69	57
241	168	14	45	222	207	0	0	20	48
164	118	282	252	88	59	49	53	6	34

Первым этапом расчётов является определение регрессионной модели изменения суммарного износа деталей шатунного подшипника. Поле корреляции суммарной величины износа деталей и наработки показаны на рисунке 8. Из графика видно, что зависимость величины износа от наработки не линейна и включает период приработки. Для практических целей важным является зона, в которой величина зазора приближается к предельному значению. Поэтому зону приработки необходимо исключить из анализа. Для этого нужно определить величину износа к моменту окончания приработки.

С этой целью на графике выделяют участок наработки от момента окончания приработки до момента, когда зависимость износа от наработки начинает отклоняться от линейной. Как следует из рисунка 24, это наработка от 15 до 90 тысяч километров пробега.

Для формирования выборки исходных данных для определения величины приработки проводят сортировку таблицы исходных данных по возрастанию наработки и выбирают данные только в диапазоне от 15 до 90 тысяч километров пробега. После этого определяют величину износа за период приработки по формулам (6) и (7). Величину приработки можно определить также как значение свободного члена в уравнении регрессии, при построении графика в Excel (в разделе работа с диаграммами – макет включить опцию добавить линию тренда (линейный прогноз) и активировать показывать уравнение на диаграмме)

Рисунок 8 – Поле корреляции суммарной величины износа деталей шатунного подшипника и пробега автомобиля

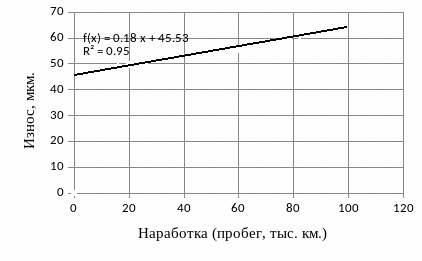
Рисунок 9 – Зависимость величины суммарного износа деталей шатунного подшипника от пробега автомобиля в период приработки и начала установившегося изнашивания

Для приведённого задания это показано на рисунке 9. Из уравнения регрессии следует, что величина приработки равна 46 мкм. При этом следует иметь в виду, что на графике для наглядности показаны экспериментальные точки в диапазоне наработки от нуля до 100 тысяч километров, а линейная аппроксимация выполнялась по экспериментальным точкам в диапазоне от 15 до 90 тысяч километров.

После определения величины износа за период приработки формируют таблицу данных для оценки параметров моделей. Для этого из массива исходных данных (таблица 4) исключают экспериментальные точки менее величины приработки (46 мкм.) и данные приводят к нормированному виду.

Далее производится выбор предполагаемых регрессионных моделей и оценка их параметров. По общему виду графика рисунка 24 можно сделать вывод о наличии нелинейности в регрессионной зависимости, а в качестве моделей можно использовать экспоненциальную, степенную функции и полином второго порядка (формулы (2), (4) и (5)).

Расчёт параметров моделей производится по формулам (8) … (13) или непосредственно при построении графика в Excel (в разделе работа с диаграммами – макет, включить опцию добавить линию тренда и активировать показывать уравнение на диаграмме).

Для разных моделей уравнения имеют следующий вид.

Экспоненциальная модель ,

степенная модель ,

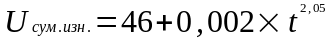полиномиальная модель

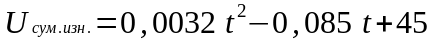
Адекватность полученных регрессионных моделей проверяют на основе дисперсионного анализа. Анализ дисперсий для различных моделей приведён в таблице 18.

Таблица 18–Анализ дисперсий моделей изменения зазора в шатунном подшипнике

Компоненты дисперсии	Сумма квадратов для моделей				Число степеней свободы		Дисперсия на одну степень свободы для моделей
	экспоненциальная	степенная	полином	экспоненциальная			степенная	полином
Общая	367034	367034	367034	76		4829		4829	4829
Факторная	398074	288540	349969	2		199037		144270	174984
Остаточная	63228	31477	28872	74		854		425	390

Как следует из расчётов (таблица 19), фактическое  значение  F-критерия  значительно больше  критического для всех моделей, следовательно, признается  статистическая  значимость всех уравнений в целом.

Выбор наиболее подходящей модели из всех статистически значимых производится с помощью коэффициента детерминации (формула (17)) и относительной ошибки (формула (16) (таблица 19.)

Таблица 19 – Критерии адекватности моделей суммарного износа деталей шатунного подшипника

Критерий	Регрессионные модели
	экспоненциальная	степенная	полином
F-критерий расчётный	233	339	448
F-критерий критический для	4,90	4,90	4,90
Коэффициент детерминации	0,83	0,96	0,92
Относительная ошибка	0,12	0,09	0,10

Как следует из таблицы 19, наиболее подходящей моделью является степенная функция, которой соответствует наибольший коэффициент детерминации и минимальная ошибка.

Вторым этапом является определение функциональной зависимости средне-квадратического отклонения от пробега автомобилей. Для этого величину пробега автомобилей (за исключением периода приработки) разбивают на интервалы. Величину интервала определяют по формуле

Для удобства дальнейших расчётов принимают величину интервала, равную 36 тысяч километров пробега автомобиля.

Затем из общего массива данных отбирают данные, попадающие в каждый интервал и определяют средне-квадратическое отклонение для каждого интервала. Результаты расчётов сводят в таблицу следующего вида (таблица 20).

Таблица 20 – Интервальные выборки суммарного износа деталей

	Выборка данных по интервалам пробега
Интервал пробега	56 -92	92-128	128-164	164-200	200-236	236-272
Величина износа, мкм.	49	53	65	70	107	167
	49	53	66	88	101	126
	48	54	67	78	114	198
	48	54	72	93	133	155
	49	57	83	85	136	182
	50	56		103	105	207
	53	55		102	157	168
	54	58		90	138	143
		62		118	126	178
		61			178	158
		59			153	223
		62				207
						238
						189
						214
						182
						198
						258
Ср. кв. откл.	2,3	3,4	7,4	14,2	24,3	33,6

Рисунок 10 – Зависимость величины средне-квадратического отклонения износа деталей от пробега автомобилей

По данным таблицы строят график зависимости средне-квадратического отклонения от пробега автомобиля и определяют функцию методом наименьших квадратов или активируя линию тренда при построении графика. График такой зависимости и функция показаны на рисунке 10.

Таблица 21 – Данные к расчёту вероятности безотказной работы

Пробег, тыс. км.	Среднее значение	Средне- квадратическое отклонение	Аргумент нормальной функции	Вероятность безотказной работы
200	150	28,5	3,1	1,00
210	161	31,7	2,5	0,99
220	173	35,1	1,9	0,97
230	185	38,6	1,4	0,92
240	198	42,4	1,0	0,84
250	211	46,3	0,6	0,74
260	225	50,4	0,3	0,62
270	239	54,6	0,0	0,51
280	254	59,1	-0,2	0,41
290	269	63,7	-0,5	0,32
300	285	68,5	-0,7	0,25
310,0	302	73,5	-0,8	0,20
320,0	319	78,7	-1,0	0,16
330,0	337	84,0	-1,2	0,12
340,0	355	89,6	-1,3	0,10
350,0	374	95,3	-1,4	0,08
360,0	394	101,2	-1,5	0,06
370,0	414	107,2	-1,6	0,05
380,0	435	113,5	-1,7	0,04

Окончательный расчёт вероятности безотказной работы производят по формуле (19). Данные к расчёту вероятности безотказной работы приведены в таблице 21 , график показан на рисунке 11 .

Рисунок 11 – Зависимость вероятности безотказной работы шатунного подшипника двигателя КамАЗ – 740 от пробега автомобиля