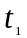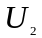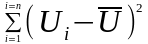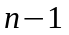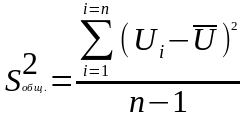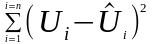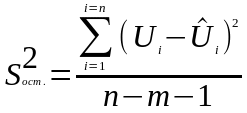- •Основы работоспособности технических систем
- •Введение
- •1 Методические рекомендации по изучению дисциплины
- •1.1 Цели и задачи освоения дисциплины
- •1.2 Место дисциплины в структуре ооп впо
- •1.3 Требования к результатам освоения содержания дисциплины
- •1.4 Структура дисциплины
- •1.5 Список рекомендуемой литературы
- •1. Основная литература
- •2. Дополнительная литература
- •3. Периодические издания
- •1.6 Рекомендации по изучению разделов дисциплины
- •1.6.1 Введение в дисциплину
- •1.6.7 Технологические способы повышения работоспособности.
- •1.6.8 Обеспечение работоспособности при эксплуатации машин.
- •1.6.9 Контрольные вопросы
- •2 Методические указания по выполнению самостоятельной работы
- •2.1 Задание
- •2.2 Теоретические пояснения
- •2.3 Методика выполнения расчётов
- •3 Отчёт о выполнении индивидуального задания
- •Приложение а
1.6.8 Обеспечение работоспособности при эксплуатации машин.
В этом разделе изучается влияние режима эксплуатации на работоспособность машин и предельные износы деталей машин. Повышение работоспособности путём применения в смазочное масло различных антифрикционных добавок.
1.6.9 Контрольные вопросы
1. Схема потери работоспособности объектов технических систем.
2. Изнашивание рабочих поверхностей деталей машин. 3. Механическое изнашивание рабочих поверхностей деталей машин.
4. Абразивное изнашивание рабочих поверхностей деталей машин.
5. Процессы изнашивания при схватывании (заедании) рабочих поверхностей деталей.
6. Коррозионно – механическое изнашивание деталей машин.
7. Окислительное изнашивание рабочих поверхностей деталей машин.
8. Кавитационные разрушения поверхностей деталей машин.
9. Коррозионные повреждения деталей машин.
10.Усталостные разрушения деталей машин.
11. Схема разрушения деталей при экстремальных нагрузках.
12. Потеря работоспособности деталей при изменении физико – механических характеристик материалов.
13. Методы повышения износостойкости рабочих поверхностей деталей.
14. Методы снижения интенсивности абразивного износа в спряжения деталей машин.
15. Методы повышения усталостной прочности деталей машин.
16. Методы повышения работоспособности при конструировании машин.
17. Технологические методы повышения работоспособности машин.
18. Методы обеспечения работоспособности машин в процессе эксплуатации.
19. Методы обеспечения работоспособности машин при ремонте.
20. Предельные значения параметров деталей машин.
21. Допустимые значения параметров деталей машин.
2 Методические указания по выполнению самостоятельной работы
2.1 Задание
Темой самостоятельной работы является исследование работоспособности узла технической системы. Расчёты производятся на примере подшипника коленчатого вала автомобильного двигателя.
Исходными данными для расчётов являются результаты измерения величины износа деталей шатунного подшипника (шейки коленчатого вала, верхнего и нижнего вкладышей). Такие измерения проводятся при ремонте двигателей, производимых при отказах, требующих разборки кривошипно–шатунного механизма. В результате для анализа составляется таблица парных значений наработки подшипника и величины износа. Варианты заданий для самостоятельной работы приведены в приложении.
2.2 Теоретические пояснения
Работоспособность объекта определяется как состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям нормативно-технической и конструкторской документации. Работоспособность считается нарушенной, если величина какого либо параметра достигнет предельного значения. Событие, заключающееся в нарушении работоспособного состояния объекта, называется параметрическим отказом.
Значения параметров по мере наработки объекта изменяются от начальных (номинальных) до предельных. Предельное состояние – состояние объекта, при котором его дальнейшая эксплуатация недопустима или нецелесообразна, либо восстановление его работоспособного состояния невозможно или нецелесообразно Значения предельных значений параметров для различных объектов устанавливаются на основе расчётов и экспериментальных исследований и указываются в нормативно – технической документации.
Причиной
изменения параметров являются процессы
старения. Основной характеристикой
процесса старения является скорость
протекания процесса
 .
Скорость изменения параметра (например,
скорость изнашивания рабочей поверхности
детали) является основным фактором,
обуславливающим случайную природу
долговечности элементов машин.
.
Скорость изменения параметра (например,
скорость изнашивания рабочей поверхности
детали) является основным фактором,
обуславливающим случайную природу
долговечности элементов машин.
В таблице 2 представлены типовые закономерности изменения процессов старения по мере наработки. Наиболее простым процессом старения является стационарный процесс, при котором скорость процесса постоянная. Зависимость степени повреждения от наработки для этих процессов – линейная функция. Такая закономерность присуща процессам изнашивания в установившейся период после приработки, процессам абразивного изнашивания рабочих органов, деталей ходовой части и другие.
Таблица 2 – Типовые закономерности процессов старения и модели приближения к отказу
Процессы |
Скорость процессов |
Накопленные
повреждения |
Модели приближения к отказам |
Стационарные постоянные |
|
|
Изнашивание |
Псевдо - стационарные |
|
|
Изнашивание при переменных режимах |
Монотонные возрастающие |
|
|
|
Монотонные убывающие |
|
|
Изнашивание в период приработки |
Экстремальные с минимумом |
|
|
|
Экстремальные с максимумом |
|
|
Коррозия, коробление |
Часто при старении возникают факторы, которые интенсифицируют или замедляют скорость процессов. Скорость монотонно может увеличиваться или замедляться. Например, увеличение зазора в сопряжениях по мере износа деталей приводит к изменению условий трения и динамических нагрузок, которые интенсифицируют процесс. В этом случае процессы накопления повреждений будут не линейны и соответственно показывают интенсификацию или замедление процессов.
Для некоторых процессов в зависимости от действующих факторов функция скорости может иметь экстремум (максимум или минимум). Такие процессы наблюдаются практически у всех сопряжений трения в период приработки, когда скорость снижается, а затем по мере изнашивания деталей постепенно возрастает.
Образование окисной плёнки на поверхности деталей из алюминиевых сплавов в первый период идёт интенсивно и затем постепенно интенсивность уменьшается. Это объясняется тем, что образование твёрдых и плотных окислов алюминия препятствует дальнейшему проникновению кислорода и скорость коррозии уменьшается.
Анализ изменения параметров состояния одноимённых деталей машин в реальных условиях эксплуатации показывает рассеивание показателей при одинаковой наработке. Это объясняется двумя факторами. Первое, это рассеивание начальных значений параметров в пределах полей допусков при изготовлении машин (твёрдость материала, шероховатость поверхностей, зазоры и натяги в сопряжениях и другие). Второе, это эксплуатационные факторы (почвенно-климатические условия, вид и интенсивность работы, уровень технического обслуживания и ремонта и другие).
Математическое описание изменения параметров технического состояния в зависимости от наработки является моделями приближения объектов к отказу.
Обоснование математической модели приближения к отказу является важной задачей исследования работоспособности технических объектов, так как от этого в конечном итоге зависит точность определения показателей – ресурса, вероятности безотказной работы и других.
Модели приближения к отказам могут быть двух типов:
– индивидуальные модели;
– среднестатистические модели.
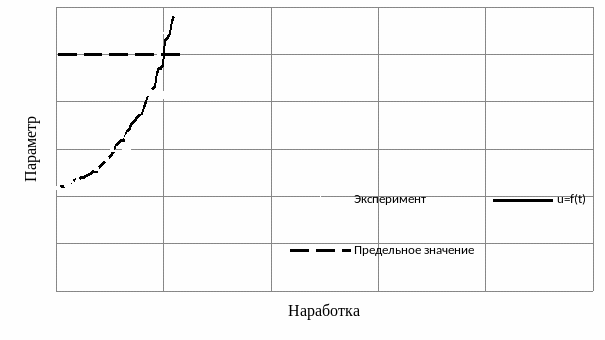
Индивидуальные модели определяются для конкретного объекта путём измерения параметров в процессе эксплуатации (рисунок 1а). Такие модели могут быть построены для объектов, измерение параметров которых может быть выполнено без демонтажных работ. Обычно измерения проводятся в моменты технического обслуживания.
|
|
Рисунок 1 –Индивидуальные (а) и среднестатистические (b) модели приближения объектов к отказам |
|
Среднестатистические модели (рисунок 1b) определяются по выборочным данным для однотипных объектов. Первый вариант – объединение в общий массив индивидуальных моделей. Второй вариант – построение моделей по данным измерений значений параметров при различных наработках для совокупности однотипных объектов. Этот вариант встречается в тех случаях, если для измерения параметра необходимо проводить демонтажные работы (например, измерение износа деталей цилиндропоршневой группы или деталей кривошипно-шатунного механизма двигателя). В этом случае для одного объекта имеется только одно измерение параметра для конкретной наработки.
Изучение связи между количественными показателями называется регрессионным анализом. Если изучается связь между двумя переменными, одну из которых можно рассматривать как аргумент, а другую как функцию, то такой анализ называют парным регрессионным. В ходе проведения регрессионного анализа подбирают математическую функцию, которая наиболее лучшим образом соответствует исходным данным, то есть обеспечивает наилучшую аппроксимацию поля корреляции. Поле корреляции – график, изображающий связь независимой и зависимой переменной. По его форме можно судить о том, какая математическая зависимость больше подходит к исходным данным.
Задача
состоит в выборе функции зависимости
значения параметра от наработки объекта,
то есть необходимо найти формулу
 .
.
Изменение параметров по мере наработки может изменяться по разным зависимостям – значение может возрастать или убывать. Однако все изменения параметров с целью упрощения моделей можно привести к возрастающей функции. Если она убывающая, то разность номинального и фактического значений будет величиной возрастающей.
Для практических целей отклонение параметров от номинальных значений желательно выражать простыми аппроксимирующими функциями. Аппроксимирующая функция должна учитывать физическую сущность процесса старения, отражать интегральный характер отклонения параметра (быть возрастающей), иметь простую форму для простоты расчётов и содержать небольшое число параметров.
Этим требованиям отвечают следующие функции.
1)
линейная функция:
 (1)
(1)
2) степенная функция: (2)
3) показательная функция: (3)
4) экспоненциальная (4)
5) полином n – порядка

(5)
Для всех случаев в качестве исходных данных имеется выборка измерений значений параметров при известных наработках (таблица 3).
Таблица 3 – Таблица исходных данных
|
|
|
... |
|
|
|
|
... |
|
Задача состоит в выборе функции, наиболее точно отражающей математическую зависимость, и физическую сущность процесса старения и оценке значений параметров, входящих в формулы (1) … (5).
Предварительно вид приближающих функций можно определить, построив точечный график и проведя линию, по возможности наилучшим образом отражающую характер расположения точек. Затем производится определение параметров выбранных функций. Обычно для этого применяется метод наименьших квадратов.
Оптимальные значения параметров определяются из условия, что сумма квадратов абсолютных разностей экспериментальных и рассчитанных по выбранной функции значений во всех точках будет минимальной.
Для
линейной функции формулы для определения
параметров
 и
и
 имеют вид:
имеют вид:
 (6)
(6)
 (7)
(7)
Для степенной, показательной и экспоненциальной функций при определении параметров необходимо предварительно вычислить значение , затем нормировать данные наблюдений (вычесть из экспериментальных данных). Начальные значения должны быть близки к нулю (значения не должны быть отрицательными или равными нулю). Таблица нормированных данных будет иметь вид (таблица 4).
Таблица 4 – Таблица исходных нормированных данных
|
|
|
... |
|
|
|
|
... |
|
Значение параметра приработки определяется по данным наблюдений в период наработки от момента окончания приработки до момента, когда наблюдается отклонение графика от линейной зависимости. Обычно этот период легко определяется по анализируемому графику. Выбрав данные за этот период, определяется по формулам (6) и (7).
После нормирования исходных данных параметры степенной функции определяются по формулам.
 (8)
(8)
 (9)
(9)
Для показательной функции.
 (10)
(10)
 (11)
(11)
Для экспоненциальной функции
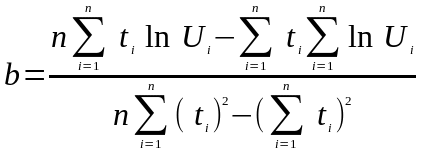 (12)
(12)
(13)
Уравнения функций с конкретными значениями параметров (после подстановке полученных значений параметров в формулы (1) … (5)) будут являться математическими моделями приближения объекта к отказу.
Проверка на адекватность
Для практического использования моделей большое значение имеет их адекватность, то есть соответствие фактическим опытным данным. Полученные математические модели необходимо проверить на адекватность.
Проверка
адекватности модели формулируется как
задача проверки предположения о том,
что значение параметра, определённого
математической моделью, отличается от
фактического не более чем на заданную
величину
 .
.
 (14)
(14)
После
вычисления будет получена совокупность
случайных величин
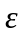 ,
среди которых могут оказаться как
величины, удовлетворяющие условию (14),
так и не удовлетворяющие ему.
,
среди которых могут оказаться как
величины, удовлетворяющие условию (14),
так и не удовлетворяющие ему.
Гипотеза об адекватности модели действительности (нулевая гипотеза, обозначаемая Н 0) может быть сформулирована как предположение о том, что полученная совокупность не даёт оснований отказаться от рассматриваемой модели. Иными словами, модель удовлетворяет заданной точности .
Альтернативная гипотеза, обозначаемая Н 1, состоит в том, что модель не отвечает заданным требованиям и, следовательно, должна быть отвергнута.
Так как
выборка
случайна, решение о выборе одной из
гипотез носит вероятностный характер.
При этом может быть допущена ошибка,
состоящая в отказе от правильной модели
(ошибка первого рода – принимается Н
1, когда верна Н 0), или ошибка, состоящая
в принятии ошибочной модели (ошибка
второго рода – принимается Н 0, когда
верна Н 1). Вероятность ошибки первого
рода – уровень значимости ( ),
это вероятность отвергнуть правильную
гипотезу при условии, что она верна. На
практике
принимают на уровне 0,05; 0,01; 0,005; 0,001.
Выбор
уровня значимости при проверке конкретной
модели зависит от ответственности
решений, принимаемых на основе
моделирования.
),
это вероятность отвергнуть правильную
гипотезу при условии, что она верна. На
практике
принимают на уровне 0,05; 0,01; 0,005; 0,001.
Выбор
уровня значимости при проверке конкретной
модели зависит от ответственности
решений, принимаемых на основе
моделирования.
Оценка значимости всего уравнения регрессии в целом осуществляется с помощью F-критерия Фишера (F-тест), основанного на дисперсионном анализе. Согласно основной идее дисперсионного анализа, общая дисперсия переменной раскладывается на две части – факторную («объяснённую») и остаточную («необъяснённую»).
Схема дисперсионного анализа и расчётные формулы приведены в таблице 5.
Таблица 5 – Таблица дисперсионного анализа
Компоненты дисперсии |
Сумма квадратов |
Число степеней свободы |
Дисперсия на одну степень свободы |
Общая |
|
|
|
Факторная |
|
|
|
Остаточная |
|
|
|
В приведённых в таблице 5 формулах:
 –
значение опытных
данных при значении аргумента
–
значение опытных
данных при значении аргумента
 ;
;
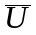 – среднее значение
выборки опытных данных;
– среднее значение
выборки опытных данных;
 – значение функции,
рассчитанное по уравнению регрессии
(модели) при значении аргумента
;
– значение функции,
рассчитанное по уравнению регрессии
(модели) при значении аргумента
;
 – объём выборки;
– объём выборки;
– число коэффициентов в уравнении регрессии.
Общая дисперсия показывает рассеивание экспериментальных данных, факторная дисперсия отображает влияние факторов, включённых модель, остаточная дисперсия отображает влияние не учтённых факторов.
Определение дисперсии на одну степень свободы приводит их к сравнимому виду. В статистике числом степеней свободы некоторой величины называют разность между количеством опытов и числом констант, найденным по этим опытам независимо друг от друга.
F-тест
(оценивание
качество модели) состоит в проверке
гипотезы H
0.
Для этого выполняется сравнение
фактического значения F-критерия
Фишера (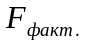 )
и
критического значения F-критерия
(
)
и
критического значения F-критерия
(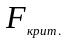 ).
).
Фактическое значение F-критерия определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы по формуле

 (15)
(15)
Критическое значение F-критерия – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости. Оно зависит от числа степеней свободы и и уровня значимости , определяется по таблицам F – распределения.
Если фактическое значение F-критерия больше критического, то признается статистическая значимость уравнения в целом. Если фактическое значение F-критерия меньше критического, полученное расхождение результатов моделирования и экспериментальных данных знáчимо (при заданном уровне значимости) и, следовательно, модель должна быть отвергнута как недостаточно точная.
Выбор наилучшей эмпирической модели
Принцип наименьших квадратов позволяет найти значения параметров модели для исследуемой экспериментальной выборки с заданным уравнением модели. Однако, чаще всего конкретная форма модели заранее неизвестна и может быть различной. Таким образом, возникает проблема выбора формы модели. Наиболее простым методом является последовательное изучение всех возможных моделей, из которых отбирается лучшая.
Одним из способов оценка качества модели является оценка по средней ошибке аппроксимации.
 (16)
(16)
В общем случае величина ошибки аппроксимации обычно не должна превышать 10-15%.
Выбор наилучшей эмпирической модели можно производить по коэффициенту детерминации. Коэффициент детерминации оценивает качество подгонки как линейных, так и нелинейных моделей и определяется по формуле.
 (17)
(17)
Коэффициент детерминации (R-квадрат) показывает, какая часть дисперсии зависимой переменной объясняется рассматриваемой моделью и принимает значения в диапазоне от нуля до единицы. Чем больше R2, тем большая часть дисперсии результативного признака объясняется уравнением регрессии, тем лучше уравнение регрессии описывает исходные данные. Таким образом, коэффициент детерминации R2 может применяться для оценки качества (точности) уравнения регрессии.
По выбранной модели приближения к отказу можно определить показатели надёжности. На рисунке 2 показана общая схема параметрических отказов.

Рисунок 2 – Общая схема приближения объектов к отказам и формирование распределения плотности вероятности наработки до отказа
Отказ
объекта наступает тогда, когда величина
параметра превысит предельное значение
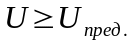 ,то есть разность
,то есть разность
 должна
быть меньше нуля. Вероятность безотказной
работы определяется уравнением
должна
быть меньше нуля. Вероятность безотказной
работы определяется уравнением
 (18)
(18)
Таким образом, для определения вероятности безотказной работы необходимо знать функцию распределения величины Y.
Обычно при расчётах принимают допущение, что распределение величины параметра в любой момент наработки является нормальным, а предельное значение величиной постоянной. Тогда вероятность безотказной работы можно определить по уравнению
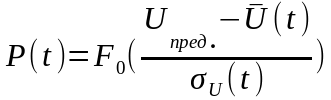 ,
(19)
,
(19)
где
 –
центрированная
нормированная функция.
–
центрированная
нормированная функция.
Задача
сводится к определению функций
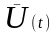 и
и
 .
Функция
является функцией приближения к отказу
и подробно рассмотрена в разделе «Работа
4. Модели приближения технических
объектов к отказам». Функцию
определяют по экспериментальным данным
в следующем порядке.
.
Функция
является функцией приближения к отказу
и подробно рассмотрена в разделе «Работа
4. Модели приближения технических
объектов к отказам». Функцию
определяют по экспериментальным данным
в следующем порядке.
Для этого наработку разбивают на несколько интервалов. Величину интервала можно, например, определить по формуле Старджесса. Затем из общего массива данных отбирают данные, попадающие в каждый интервал. По данным выборки данных для каждого интервала определяется средне – квадратическое отклонение и методом наименьших квадратов определяется функция .




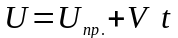


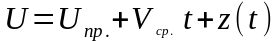




 Изнашивание
Изнашивание



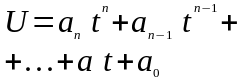 Ползучесть,
изнашивание, коррозия
Ползучесть,
изнашивание, коррозия