1.5.2. Расчет термодинамических функций сольватации методами компьютерного моделирования

В методах молекулярной динамики (МД) и Монте Карло (МК) взаимодействия между частицами в системе описываются различными потенциалами. Параметры этих потенциалов могут быть получены из эксперимента, например, жесткость связи рассчитывают на основе силовых констант по данным ИК-спектров, либо из ab initio квантовохимических расчетов (геометрия, заряды), либо могут подбираться так, чтобы симуляции как можно лучше воспроизводили различные свойства реальных веществ: плотность, температуру, энтальпию испарения, коэффициенты диффузии.

В методе Монте-Карло (алгоритм Метрополиса) на каждом шаге генерируются небольшие случайные изменения координат частиц, при этом вероятность принятия этих изменений пропорциональна еxp(–ΔE/kT), если ΔE>0, и 1, если ΔE<0. Если шаг принят, то новая конфигурация добавляется к фазовой траектории системы. Метод молекулярной динамики основан на решении уравнений классической механики на небольших (1-2 фс) отрезках времени, исходя из известных потенциалов взаимодействий и случайно сгенерированных начальных скоростей всех частиц. Он часто применяется для изучения фолдинга белков, диффузионных процессов. Используя оба метода, можно напрямую изучать состав окружения каждой молекулы в растворе, предсказывать вид функций радиального распределения, рассчитывать на основании тех или иных критериев число водородных связей между различными молекулами.

Эти методы могут применяться и для расчета термодинамических функций сольватации. Теоретически для расчета энтальпии сольватации мы бы могли усреднить значение энтальпии системы с растворенным веществом и без него по достаточно длинным траекториям, однако на самом деле флуктуации этих значений намного превысят величины энтальпий сольватации. Вычисление же энергии Гиббса подобным способом принципиально невозможно. Поэтому прибегают к использованию таких методов, как метод возмущений свободной энергии (FEP) и термодинамическое интегрирование (TI).

В методе FEP переход от начального состояния λ = 0 к конечному λ = 1 трактуется как серия дискретных изменений потенциалов взаимодействий. Например, для описания сольватации в состоянии λ = 0 растворенное вещество не взаимодействует с растворителем, а в последующих состояниях величины потенциалов всех невалентных взаимодействий между растворенным веществом и растворителем могут составлять 10%, 20%, 30% и т.д. от полного потенциала, достигая 100% в состоянии λ = 1. Для каждого из состояний проводится отдельная симуляция, на каждом шаге которой рассчитывается не только энергия при текущем значении параметра λ , но и энергия при потенциале, соответствующем следующему шагу . Энергия Гиббса при переходе системы от начального состояния к конечному рассчитывается по уравнению:

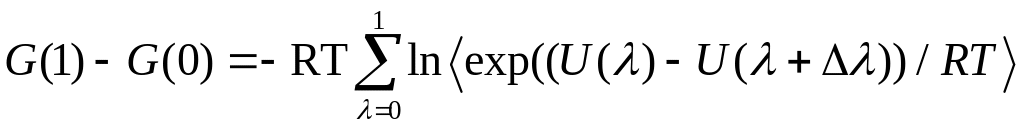. (29)

Точность расчета тем выше, чем меньше шаг изменения λ.

В методе термодинамического интегрирования переход к конечному состоянию разбивается на шаги аналогичным образом, а изменение энергии Гиббса рассчитывается по формуле:

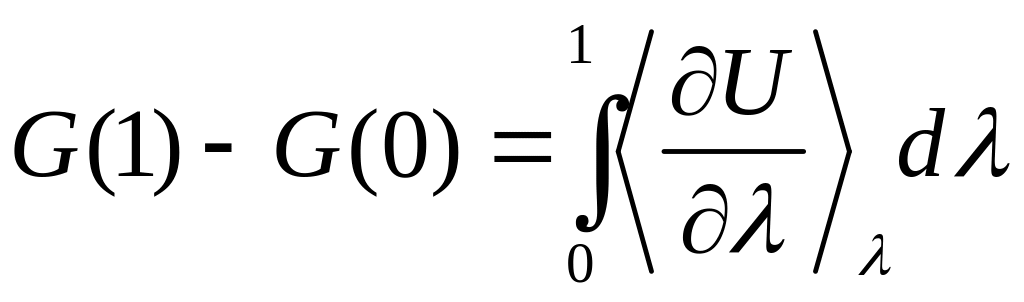. (30)

Применение этих методов дает хорошо согласующиеся с экспериментальными данными энергии Гиббса гидратации различных алканов и спиртов [67, 68]. Для расчета энтальпии сольватации можно использовать температурную значимость энергии Гиббса от температуры (ур-е 20), однако ошибка этого расчета всегда будет намного выше, чем для энергии Гиббса.

Большой интерес для расчета термодинамических функций сольватации одноатомных молекул и частиц с заданным произвольным потенциалом взаимодействия (в частности, жестких сфер) представляет метод вставки частиц Видома [69]. Для каждой конфигурации из траектории симуляции растворителя производится большое число вставок изучаемой частицы в случайно выбранные точки пространства, при этом рассчитывается изменение потенциальной энергии. Для нахождения избыточного по сравнению с идеальной газовой фазой химического потенциала проводится усреднение по всем вставкам во все конфигурации. В случае NPT-ансамбля формула расчета имеет вид:

, (31)

где ΔU – изменение потенциальной энергии при каждой вставке частицы, V – объем системы. Точность метода зависит от числа вставок и длины траектории, результаты хорошо воспроизводятся уже при 10⁵ вставок на каждую конфигурацию. Величины, полученные этим методом для сольватации инертных газов и метана (в модели с объединенными атомами углерода и водорода) в воде, хорошо воспроизводят эксперимент [70] При этом вычислительные затраты гораздо меньше, чем в методах пертурбации свободной энергии и термодинамического интегрирования. Метод, однако, неприменим для частиц слишком большого размера, например, для расчета энергий образования полостей большого размера из-за ничтожной вероятности их появления в жидкости за время симуляции, а также для многоатомных молекул.