1.5. Методы расчета термодинамических функций растворения в смешанных растворителях

Теоретическое предсказание энергий растворения в водно-органических смесях – сложная задача. Существующие модели сольватации, в том числе эмпирические, предназначаются в первую очередь для описания свойств растворов в индивидуальных растворителях, при этом даже для растворов в чистой воде часто требуется использование специальных наборов параметров или уравнений. Для успешного расчета термодинамических функций сольватации в водно-органических смесях обязательно учитывать локальный состав растворителя вокруг растворенной молекулы (предпочтительную сольватацию). Такие универсальные методы, как МД- и МК-моделирование, требуют дополнительной оптимизации параметров взаимодействий для удовлетворительного воспроизведения экспериментальных физических свойств водно-органических смесей.

Поэтому ни один из предсказательных методов нельзя рассматривать как источник данных о сольватационных свойствах водно-органических смесей. Тем не менее, они полезны для проверки различных гипотез о молекулярном механизме сольватации и структуре окружения растворенной молекулы на основе экспериментальных данных. Ниже мы кратко рассмотрим некоторые из них.

1.5.1. Методы расчета термодинамических функций сольватации в водно-органических смесях

Существует множество уравнений и моделей для расчета энергии Гиббса растворения/сольватации в различных растворителях. Среди них теория регулярных растворов Гильдебранда [58], уравнение NTRL [59], модель UNIQUAC [60], групповые модели UNIFAC [61] и ASOG [62], корреляционные уравнения Абрахама [63]. Однако попытки применения большинства из них как к воде, так и к водно-органическим средам приводит к большим отклонениям от экспериментальных результатов.

Большее развитие получили чисто эмпирические методы оценки растворимости в водно-органических смесях на основе данных о растворимости в чистых компонентах смеси. Это связано с задачей определения растворимости лекарственных соединений в большом числе смесей различного состава, что делает прямые экспериментальные измерения трудоемкими и дорогостоящими.

Рассмотрим два таких метода:

1. Метод Ялковского [64]. Расчет растворимости в смешанном растворителе проводится, исходя из данных по растворимости в растворителях 1 и 2 (X₁ и X₂, соответственно) и состава растворителя (f₁ и f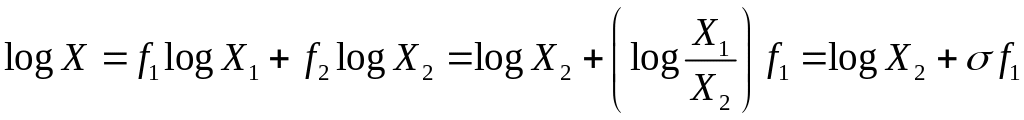₂)

. (22)

В работе [65] была показана линейная зависимость между σ и коэффициентом распределения октанол-вода (logK_ow). σ выражается уравнением

, (23)

где M и N константы сорастворителя и не зависят от природы растворенного вещества. Метод в среднем дает погрешность, бо́льшую точности экспериментального определения растворимости (около 10%) и допустимых ошибок в фармацевтике (примерно 30%), однако является очень простым и требует минимального числа исходных данных.

2. Расширенная модель растворимости Гильдебранда. Мартинс и сотр. [66] модифицировали модель регулярных растворов, добавив в нее эмпирический параметр взаимодействия растворенное вещество-растворитель (WW). Это позволило расширить область применения модели. Выражение для растворимости выглядит следующим образом:

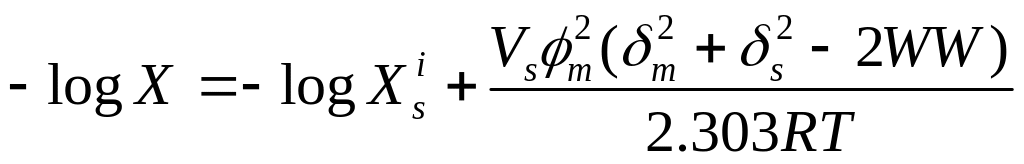, (24)

где – идеальная растворимость вещества (растворимость в идеальном растворе, когда только кристалличность вещества ограничивает растворимость), – мольный объем вещества, – объемная доля растворителя (принимается равной единице из-за малых количеств растворенного вещества). WW рассчитывается разложением степенного ряда WW = ∑ A_iδ_m, где δ_m = f₁δ₁ + f₂δ₂ (22), δ₁ и δ₂ – параметры Гильдебранда чистых растворителей. Метод требует знания большого количества экспериментальных данных: энтальпии и энтропии испарения, плотности, идеальной растворимости, а также оценки δ_S. Все это, а также зависимость δ_S от полярности растворителя затрудняет использование данного метода.

Для энтальпий сольватации инертных газов и углеводородов в неводных бинарных растворителях Батовым была показана [44] связь с плотностью энергии когезии растворителя. Избыточная энтальпия растворения по отношению к аддитивной по составу величине выражается уравнением:

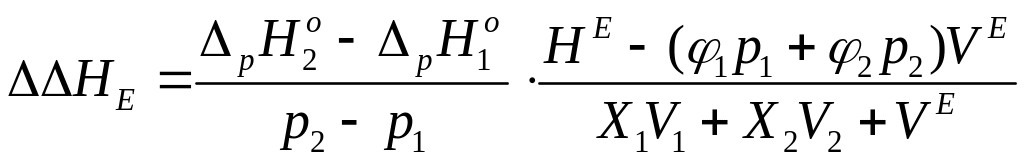, (25)

где и – стандартная энтальпия растворения вещества в растворителе 2 и 1, – избыточный объем смеси, , – мольные доли компонентов смеси, p₂, p₁ – плотности энергии когезии растворителя 2 и 1 соответственно, φ₂, φ₁ – объемные доли компонентов смеси, H^E – избыточная энтальпия. Плотность энергии когезии выражается через энтальпию испарения растворителя:

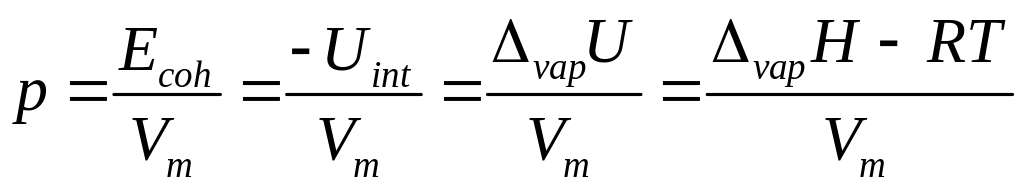. (26)

Для водно-органических смесей данное уравнение неприменимо. При этом, в частности, сольватация ксенона в смесях воды со спиртами хорошо описывается квадратным уравнениями вида

_сН^о = a₀ + a₁ р + a₂ р², (27)

_сН^о = b₀ + b₁ р + b₂ р² - 13.0 Х₁, (28)

где p – плотность энергии когезии растворителя, X₁ – мольная доля воды, а a_i и b_i – подгоночные коэффициенты. Для аргона энтальпия сольватации хорошо описывается только кубическим уравнением.

Для алканов в смесях воды с апротонными растворителями отклонение энтальпии растворения от аддитивного по составу растворителя значения с хорошей точностью (R²=0.9896) описывается сложной зависимостью от мольного объема углеводорода и избыточной плотности энергии когезии. Для описания теплового эффекта растворения бензола в смесях воды с апротонными растворителями использовались [41] сразу два уравнения: до максимума энтальпия хорошо описывается линейной зависимостью от избыточной плотности энергии когезии (р^Е_ат), а от максимума и до чистой воды ∆∆Н^Е пропорциональна (р_ат^E)².

Эти эмпирические и корреляционные уравнения, однако, не позволяют прояснить физическую природу максимума энтальпии сольватации при определенном содержании воды в смеси, или же получить какую-либо информацию о предпочтительной сольватации.