3.3. Молекулярно-динамическое моделирование сольватации в водно-органических смесях

Процесс сольватации часто разделяют на два гипотетических этапа: формирование полости в растворителе, позволяющей разместить молекулу растворенного вещества, и последующий перенос вещества в эту полость. Изменение энергии для второй стадии представляет собой средневзвешенную энергию взаимодействия растворенного вещества с молекулами сорастворителей, находящимися вокруг полости. Энергия первой стадии (образования полости) может включать в себя как вклад разрыва межмолекулярных взаимодействий внутри жидкой фазы, так и энергию реорганизации растворителя, приводящей к предпочтительной сольватации полости одним из сорастворителей.

Нами был произведен расчет термодинамических функций сольватации инертных газов – неона и ксенона с помощью методов молекулярной динамики. При расчете использовался метод вставки Видома (см. главу 1.5.2). Инертные газы, как и алканы, способны вступать только в дисперсионные взаимодействия с растворителем. При этом процесс образования сферической полости в растворителе, необходимой для размещения атома инертного газа, может быть смоделирован сольватацией жесткой сферы, полностью исключающей центры любых атомов из радиуса, соответствующего размеру атома инертного газа. Это дает возможность рассчитать термодинамические функции образования полости и взаимодействия с растворителем по отдельности.

Молекулярно-динамическое моделирование было проведено с помощью программы GROMACS версии 5.1 [80]. Во всех симуляциях использовалась модель воды SPC/E [81]. Для каждого сорастворителя из литературы были выбраны такие силовые поля, чтобы в симуляциях наилучшим образом воспроизводились экспериментальные свойства смесей с водой, в первую очередь их плотность, а также не происходило разделения фаз. Список этих силовых полей представлен в таблице 6. Во всех случаях использовались стандартные для данного силового поля параметры связей, углов и двугранных углов.

Таблица 6. Силовые поля, использованные для моделирования сорастворителей

Органический сорастворитель	Силовое поле	Модель атомов*	Комбинационное правило	Ссылка
Тетрагидрофуран	TraPPE	UA	Лорентц-Бертло	[82]
Ацетон	KBFF	UA	Среднегеометрическое	[83]
Ацетонитрил	AMBER	AA	Лорентц-Бертло	[84]
Диметилсульфоксид	OPLS	UA	Среднегеометрическое	[85]

^*UA – модель с объединенными с водородами псевдо-атомами углерода, отражающими взаимодействие группы атомов типа CH_n, AA – модель с явно заданными атомами водорода.

Радиус отсечения для ближних кулоновских и ван-дер-Ваальсовых взаимодействий составлял 1.0 нм. Для расчета дальних электростатических взаимодействий использовался метод PME. Постоянная температура поддерживалась с помощью термостата с масштабируемыми скоростями (v-rescale), постоянное давление – баростатом Парринелло-Рахмана. Сочетание использованных моделей и параметров хорошо воспроизводит свойства смесей во всем диапазоне концентраций. Плотности смесей представлены в таблице 7.

Таблица 7. Экспериментальные и полученные в МД симуляциях плотности водно-органических смесей при температуре 298.15 К

x1	ρ (MD), г/мл	ρ (exp) [86], г/мл	x1	ρ (MD), г/мл	ρ (exp) [87], г/мл
Диметилсульфоксид			Ацетон
0.0	0.997	0.998
0.1	1.038	1.042	0.1	0.963	0.957
0.2	1.060	1.072	0.2	0.931	0.925
0.3	1.074	1.088	0.3	0.905	0.898
0.4	1.083	1.095	0.4	0.884	0.874
0.5	1.088	1.097	0.5	0.866	0.853
0.6	1.090	1.096	0.6	0.850	0.835
0.7	1.092	1.095	0.7	0.837	0.820
0.8	1.092	1.096	0.8	0.827	0.807
0.9	1.093	1.096	0.9	0.817	0.795
1.0	1.095	1.096	1.0	0.810	0.785
x1	ρ (MD), г/мл	ρ (exp) [88], г/мл	x1	ρ (MD), г/мл	ρ (exp) [89], г/мл
Ацетонитрил			Тетрагидрофуран
0.1	0.957	0.991	0.1	0.980	0.978
0.2	0.919	0.983	0.2	0.963	0.959
0.3	0.890	0.967	0.3	0.947	0.943
0.4	0.865	0.936	0.4	0.933	0.929
0.5	0.844	0.912	0.5	0.921	0.918
0.6	0.827	0.890	0.6	0.910	0.908
0.7	0.812	0.866	0.7	0.901	0.899
0.8	0.799	0.843	0.8	0.894	0.893
0.9	0.788	0.819	0.9	0.888	0.887
1.0	0.779	0.796	1.0	0.884	0.883

Для каждого органического сорастворителя было подготовлено 10 кубических ячеек с периодическими граничными условиями с мольной долей воды от 0 до 1 с шагом 0.1. Каждая ячейка суммарно содержала 1000 молекул растворителей. Для каждого состава было проведено семь запусков при температурах от 283 до 313 К с шагом 5 К. При запуске система сначала минимизировалась, уравновешивалась в течение 200 пс при постоянном объеме и 2 нс при постоянном давлении 1 бар. После записывалась траектория длительностью 10 нс (давление 1 бар).

Эта траектории использовалась для расчета энергии Гиббса вставки неона и ксенона, а также жестких сфер радиусом 0.28 и 0.345 нм, что соответствует размеру атомов неона и ксенона [90]. Вставка производилась 100000 раз через каждую 1 пс траектории. Поскольку рассчитываемое программой по формуле (31) значение соответствует стандартному состоянию с равной молярной концентрацией растворяемого вещества в жидкой и газовой фазах, для перевода результата к мольно-долевому стандартному состоянию использовалась формула

. (39)

Энтропия сольватации рассчитывалась по температурной зависимости энергии Гиббса сольватации:

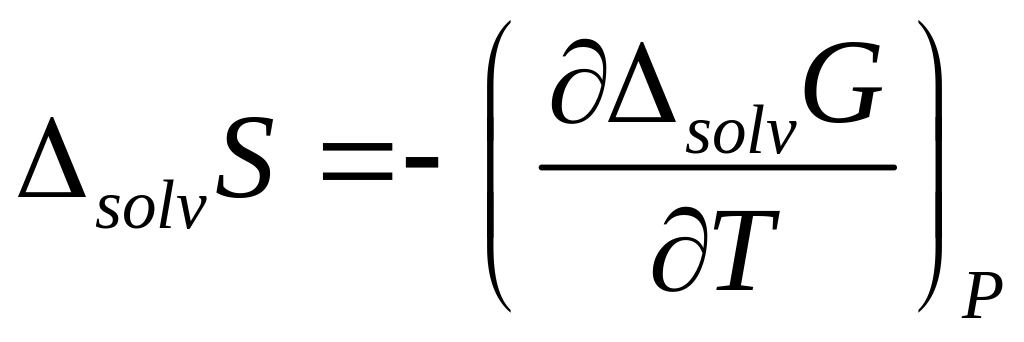. (40)

По данным об энтропии и энергии Гиббса проводился расчет энтальпии сольватации:

. (41)

Для проведения расчетов использовался персональный компьютер с процессором Intel Core i7 c тактовой частотой 3.3 ГГц.

Полученные зависимости расчетных значений термодинамических функций сольватации инертных газов и жестких сфер в водно-органических смесях от состава растворителя представлены на рисунках 17-19. Необходимо отметить, что рассчитанные значения энергий Гиббса сольватации для неона и ксенона в воде и в чистых органических растворителях хорошо согласуются с экспериментальными данными (табл. 8). Так как размер жестких сфер соответствуют полости, необходимой для размещения в ней инертного газа, можно вычислить термодинамические функции взаимодействия инертный газ-растворитель: (42).

Таблица 8. Рассчитанные и экспериментальные значения энергий Гиббса сольватации неона и ксенона в чистых растворителях при 298 К

Растворяемое вещество Растворитель	Ne		Xe
	/ (кДж/моль)	/ (кДж/моль)	/ (кДж/моль)	/ (кДж/моль)
Ацетон	22.5	21.7 [91]	14.4	11.5 [91]
Ацетонитрил	24.6	–	15.4	14.1 [92]
Диметилсульфоксид	26.7	25.3 [91]	17.3	15.8 [91]
Тетрагидрофуран	22.4	22.7 [93]	13.6	10.9 [93]
Вода	29.6	29.1 [94]	26.2	23.3 [94]

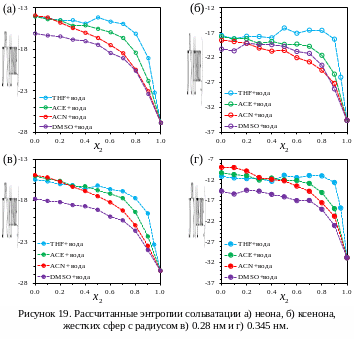
Результаты моделирования показывают, что максимумы энтальпий сольватации, наблюдаемые в эксперименте с углеводородами, а также вид зависимости энергии Гиббса и энтропии сольватации воспроизводятся в симуляциях как для инертных газов, так и для жестких сфер. В смеси диметилсульфоксид-вода максимумы менее выражены, чем в смеси тетрагидрофуран-вода, а в смеси воды с ацетонитрилом они вообще не наблюдаются, а происходит уменьшение энтальпии сольватации с увеличением концентрации воды.

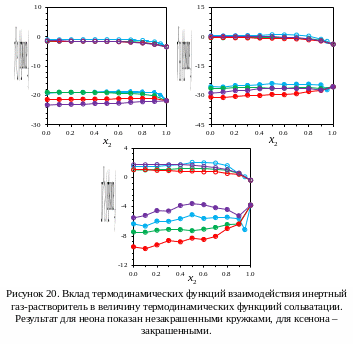
Как показано на рисунке 20, вклад взаимодействия в энтальпию сольватации, в отличие от вклада образования полости, для неона и ксенона не имеют максимума при высоких концентрациях воды. Вместо этого как энтальпии, так и свободные энергии Гиббса взаимодействий с растворителем незначительно меняются в широком диапазоне составов растворителей и начинают уменьшаться только при очень высоких концентрациях воды (80-90 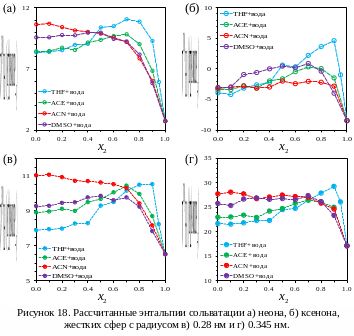мол.%). Наиболее вероятным объяснением такого поведения является то, что сольватная оболочка при более низких концентрациях состоит в основном из молекул органического сорастворителя, так что энергия взаимодействий растворенного вещества с ним остается почти такой же, как в чистом органическом растворителе. Анализ окружения ксенона (с радиусом 0.6 нм) в прямом моделировании его растворов показал, что во всех смесях концентрация органического сорастворителя в сольватной оболочки выше среднего состава раствора. Так в смеси, содержащей 20% тетрагидрофуран, молярная доля органического растворителя вокруг ксенона составляла около 47%, а в смеси с 20% ацетона – 36%.

Состав сольватной оболочки вокруг полости все более и более отличается от среднего состава растворителя по мере увеличения мольной доли воды (вплоть до определенного ее значения). Энтальпийные затраты на поддержание полости, окруженной органическим сорастворителем, растут, потому что в процесс реорганизации смеси вовлекается все большее число молекул, что приводит к росту энтальпии образования полости. Поскольку смесь обогащается водой, при определенном составе смеси затраты на реорганизацию становятся слишком велики, чтобы скомпенсировать их энтропийным фактором. В этот момент начинается падение энтальпий сольватации с дальнейшим ростом содержания воды.

Графики против для расчетных данных приведены на рисунке 21. Качественно они обнаруживают сходство с графиками 11,13 для экспериментальных значений термодинамических функций сольватации углеводородов. В широком диапазон составов наблюдается линейная компенсация между энтропией энтальпией. Как и в случае с углеводородами, вид кривых для смеси ацетонитрил-вода существенно отличается от других систем.

Линейная компенсация во всех системах, кроме смесей с ацетонитрилом, сохраняется до концентраций органического сорастворителя порядка 20-25%. После этой критической концентрации происходит загиб кривой: зависимость vs стремится к значения для чистой воды.

Таким образом, зависимости термодинамических функций сольватации от состава растворителя, полученные в результате моделирования процесса сольватации как инертных газов, так и жестких сфер, обнаруживают сходство с экспериментально наблюдаемыми зависимостями для растворов углеводородов. Подавление гидрофобного эффекта небольшим количеством органического сорастворителя оказывается связано только со вкладом образования полости.