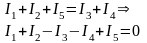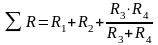3. Закон Ома для электрических цепей постоянного тока
Носителями тока в металлах являются свободные электроны. Наряду со свободными электронами, в металлах имеются положительные заряды – ионы, расположенные в узлах кристаллической решетки и не принимающие участие в переносе тока. При отсутствии внешнего электрического поля, свободные электроны движутся хаотически, и ток в металле равен нулю. При наличии электрического поля они приобретают дополнительное упорядоченное движение (дрейф) против поля, создавая электрический ток.
Электроны движутся не свободно, а испытывают соударение с ионами кристаллической решетки, что тормозит их поступательное движение.
Сопротивление проводника – противодействие проводника направленному движению зарядов, т.е. электрическому току [3, ст. 17-18].
Закон Ома для участка цепи. Георгом Омом (1826 г.) экспериментально было установлено, что сила тока на участке цепи (рис. 1.2) прямо пропорциональна напряжению, приложенному к концам этого участка, и обратно пропорциональна его сопротивлению (1.9) [3, ст. 18]:
|
|
Рис. 1.2. Участок цепи |
где, R – сопротивление, Uаb – напряжение на участке цепи а-b |
Закон Ома можно сформулировать и относительно тока (1.10) [5, ст. 16]:
I=Ug; (1.10)
где G – проводимость, величина обратная сопротивлению и определяется по формуле (1.5).
Геометрической интерпретацией закона Ома является вольт-амперная характеристика (ВАХ). Для линейного элемента она имеет вид прямой (рис. 1.3) [5, ст. 16]:

Рис. 1.3. Вольт-амперная характеристика [5, ст. 16].
Закон Ома для полной цепи. Сила тока в цепи прямо пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления (1.12):
 ,
А; (1.12)
,
А; (1.12)
где E – ЭДС источника напряжения,
R – сопротивление всех внешних элементов цепи,
r – внутреннее сопротивление источника напряжения.
Сопротивление проводника зависит от материала, из которого изготовлен проводник, его размеров и геометрической формы, а также от температуры (1.13):
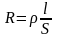 , (1.13)
, (1.13)
где ρ – удельное сопротивление, т.е. сопротивление проводника единичной длины с единичной площадью сечения;
l – длина проводника;
S – площадь поперечного сечения [1].
4. Законы Кирхгофа
Два правила Кирхгофа полностью определяют электрическое состояние цепи и дают основу для их расчетов.
I – й закон Кирхгофа: алгебраическая сумма токов в любом узле электрической цепи равна нулю (1.14) [1, ст. 12; 2, ст. 11].
 ; (1.14)
; (1.14)
Т. е. в любом узле цепи сумма приходящих токов равна сумме уходящих токов (рис. 1.4) (1.15):
|
|
(1.15) |
Рис. 1.4. Электрический узел
Если ток направлен в узел, то перед ним в уравнении ставится « + », если ток направлен от узла, то « – » [2, ст. 11].
II – й закон Кирхгофа: алгебраическая сумма напряжений для любого замкнутого контура равняется алгебраической сумме ЭДС контура.
Рассмотрим простейшую цепь с последовательным соединением проводников, приведенную на рисунке 1.5. В представленной схеме известны все сопротивления и ЭДС. Через все сопротивления проходит один и тот же ток. Суммарное сопротивление схемы равняется сумме всех |
Рис. 1.5. Цепь с последовательным соеди-нением проводников |
сопротивлений:
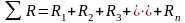 ,
[6].
,
[6].
По закону Ома, ЭДС в результирующей цепи равняется произведению силы тока на результирующее сопротивление(1.16):
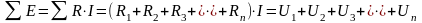 ; (1.16)
; (1.16)
где
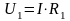 ,
,
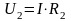 и т.д. и в результате чего мы получаем
второй закон Кирхгофа (1.16):
и т.д. и в результате чего мы получаем
второй закон Кирхгофа (1.16):
 ; (1.17)
; (1.17)
При смешанном соединении проводников, представленном на рисунке 1.6, преобразование схемы производят в следующем порядке. Сначала преобразуют сопротивления, соединенные параллельно (R3 и R4), а затем производят преобразования для сопротивлений, соединенных последовательно (1.18):
Рис. 1.6. Цепь со смешанным соединением проводников |
|
(1.18)
|

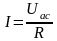 ,
А (1.9)
,
А (1.9)