Контрольная работа №1 Преобразование чисел из одной системы счисления в другие
Осуществить переводы заданных целых чисел в соответствии с указанными последовательностями преобразований из одной системы счисления в другие.
Варианты индивидуальных заданий
Реализовать заданные цепочки переводов целых чисел
1.
А.
Б.
В.
2.
А.
Б.
В.
3.
А.
Б.
В.
4.
А.
Б.
В.
5.
А.
Б.
В.
6.
А.
Б.
В.
7.
А.
Б.
В.
8.
А.
Б.
В.
9.
А.
Б.
В.
10.
А.
Б.
В.
11.
А.
Б.
В.
12.
А.
.
Б.
В.
13.
А.
Б.
В.
14.
А.
Б.
В.
15.
А.
Б.
В.
16.
А.
Б.
В.
17.
А.
Б.
В.
18.
А.
Б.
В.
19.
А.
Б.
В.
20.
А.
Б.
В.
21.
А.
Б.
В.
22.
А.
Б.
В.
23.
А.
Б.
В.
24.
А.
Б.
В.
25.
А.
Б.
В.
26.
А.
Б.
В.
27.
А.
Б.
В.
28.
А.
Б.
В.
29.
А.
Б.
В.
30.
А.
Б.
В.
31.
А.
Б.
В.
32.
А.
Б.
В.
33.
А.
Б.
В.
34.
А.
Б.
В.
35.
А.
Б.
В.
36.
А.
Б.
В.
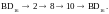
37.
А.
Б.
В.
38.
А.
Б.
В.
39.
А.
Б.
В.
40.
А.
Б.
В.
41.
А.
Б.
В.
42.
А.
Б.
В.
43.
А.
Б.
В.
44.
А.
Б.
В.
45.
А.
Б.
В.
46.
А.
Б.
В.
47.
А.
Б.
В.
48.
А.
Б.
В.
49.
А.
Б.
В.
50.
А.
Б.
В.
Пример выполнения задания
Реализовать заданную цепочку переводов целых чисел:
21810 → 2 → 8 → 21810.
Решение
Для перевода десятичного числа 21810 в двоичную систему счисления последовательно выполняем операции целочисленного деления на 2 и фиксируем остатки:
2 |
1 |
8 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
8 |
1 |
0 |
9 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
8 |
|
5 |
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
4 |
|
2 |
7 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2 |
6 |
|
1 |
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
2 |
|
|
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
6 |
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
Результат: последовательность остатков от деления, взятых в обратном порядке:
21810 = 110110102.
Для перевода двоичного числа 110110102 в восьмеричную систему счисления разбиваем исходное двоичное число слева направо на триады и заменяем каждую триаду эквивалентной восьмеричной цифрой:
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
3 |
|
|
3 |
|
|
2 |
|
Результат:
110110102 = 3328.
Для перевода восьмеричного числа 3328 в десятичную систему счисления выполняем умножение значений разрядов восьмеричного числа на 8i и складываем результаты:
3328 = 2×80 + 3×81 + 3×82 = 2 + 24 + 192 = 21810.
Задание выполнено.