2˂ 10 Следовательно работаем с теор. Пуассона

Р200(4)= = 0,0902 ( по таблице Пуассона значений функций).

Задача: На факультете насчитывается 1825 студентов. Какова вероятность, что 1 сентября является днем рождения 4-х студентов?

n = 1825

m= 4

p=

• = 1825 * = 5

5˂10 Следовательно теорема Пуассона

Р1825(4)= = 0,1755.

Локальная теорема Муавра Лапласа. Если n неограниченно возрастает, а р бесконечно мало, но отлично от 0 и 1 (не равно 0,1), то вероятность того, что в n независимых испытаниях события А наступит m раз вычисляется по формуле:

Рn(m) ≈ * * – f(x)- функция Гауса (Ф-я четная, монотонно невозрастающая_

x =

Задача: В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей 300 имеют холодильники.

Решение:

n= 400

m= 300

p = 0,8

q= 0,2

• =400 * 0,8 = 320≥10

x = = = = = - = -2,5(искать по таблице значений функции Гауса)

f (-2,5) = 0,0175

P400(300) * 0,0175( вставили в формулу)

Задача: При обследовании уставных фондов банка установлено, что пятая часть банков имеют уставной фонд свыше 100 000 000 руб. Найти вероятность того, что среди 1800 банков имеют уставной фонд свыше 100 000 000 руб. 300 банков.

Решение:

n = 1800

m= 300

p = = 0,2

• = 1800*0,2=360˃10-не работает теорема Пуасона.

x = = = = = = -3,57

f(3,57)=0,0007

Р1800(300)= * 0,0007= = 0,00004

Задача: По результатам проверок налоговыми инспекциями установлено, что в среднем каждое второе малое предприятие региона имеет нарушение финансовой дисциплины. 1)Найти вероятность того, что из тысячи 480 будут иметь нарушения дисциплины.2)Найти вероятнейшее число таких предприятий.

Решение

n = 1000

m=480

p=0,5 (q)

• = 500˃10

Локальная теор. Муавра Лапласа

x = = 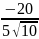= = -1,26

f(-1,26)= 0,1804(по табл.)

Р1000(480) = * 0,1804 = 0,0114

2) 1000 * 0,5 – 0,5≤ m0 ≤ 1000* 0,5 +0,5

499,5 ≤ m0 ≤ 500,5

m 0 = 500

11.Интегральная предельная теоремы Муавра-Лапласа. Следствие интегральной предельной теоремы Муавра-Лапласа.

Интегральная предельная теоремы Муавра-Лапласа.

Если n неограниченно возрастает, а р бесконечно мало и не равно 0 и 1, то вероятность того, что в n независимых испытаниях событие А произойдет не менее А раз, но не более В раз вычисляется по формуле:

Р (а ≤ m ≤ b) = Ф (Х2) – Ф (Х1) (формула А)

Если тут 2,то формулу А делим на

Ф(х) = dt

1. Функция Ф(х) нечетная.

2. Функция Ф(х) монотонно неубывающая

,  .

Задача: Найти вероятность того, что из 1800 банков имеют уставной фонд свыше 100 000 000 от 300 до 400 банков включительно.

а = 300

в = 400

Р (300 ≤ m ≤ 400 ) = Ф (2,36) – Ф (-3,57) = Ф (2,36) + Ф (3,57) = 0,4909 + 0,499841 = 0, 990741

Х1 = = = = -3,57

Х2 = = = = 2,36

Задача: Строительная фирма занимающаяся строительством коттеджей раскладывает рекламные листки по ящикам. Прежний опыт работы показывает, что примерно в одном случае из двух тысяч следует заказ. Найти вероятность того, что при размещении 100 000 листовок число заказов будет:

А) равно 48

Б)находится в границах от 45 до 55.

Решение:

а) n = 100 000

m = 40

p =

q =

λ = n * p = 50 ˃10

x = = = - 0,28

f = (-0,28) = 0,3836

P100 000 (48) = * 0,3836 = = 0,0054

Б) n = 100 000

45≤ m≤ 55

p =

q =

P(45≤m≤55) = Ф (0,707) – Ф ( -0,707) = Ф (0,707) + Ф (0,707) = 2Ф (0,707)= 2* 0,4564 =0,9128

Х1 = 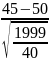= = 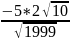0,707

Х2 = = 0,707

Рассмотрим следствие интегральной теоремы Муавра­Лапласа.

Следствие. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе n независимых испытаний вероятность того, что:

а) число m наступлений события А отличается от произведения nр не более, чем на величину ε > 0 (по абсолютной величине), т.е. ;

б) частость  события А заключена в пределах от α до β (включительно), т.е.  , Где  , .

в) частость  события А отличается от его вероятности р не более, чем на величину Δ > 0 (по абсолютной величине), т.е.  .

□ 1) Неравенство  равносильно двойному неравенству пр - Е ~ т ~ пр + Е. Поэтому по интегральной формуле :

.

2) Неравенство  равносильно неравенствуa ≤ m ≤ b при a = nα и b = nβ. Заменяя в формулах  и , величины а иb полученными выражениями, получим доказываемые формулы  и , .

3) Неравенство  равносильно неравенству . Заменяя в формуле , получим доказываемую формулу .

Пример. По статистическим данным в среднем 87% новорожденных доживают до 50 лет. Найти вероятность того, что из 1000 новорожденных доля (частость) доживших до 50 лет будет: а) заключена в пределах от 0,9 до 0,95; б) будет отличаться от вероятности этого события не более, чем на 0,04 (по абсолютной величине)?

Решение. а) Вероятность р того, что новорожденный доживет до 50 лет, равна 0,87. Т.к. n = 1000 велико (условие npq = 1000·0,87·0,13 = 113,1 ≥ 20 выполнено), то используем следствие интегральной теоремы Муавра-Лапласа. Вначале определим:

,  . Теперь по формуле :

.

Б) По формуле  :

. Так как неравенство  равносильно неравенству , полученный результат означает, что практически достоверно, что от 0,83 до 0,91 числа новорожденных из 1000 доживут до 50 лет.