Тема 3. Множественная корреляция
Найти выборочное уравнение прямой линии регрессии Y на Х по данным, приведенным в корреляционной таблице.
Y |
X |
ny |
|||||
20 |
25 |
30 |
35 |
40 |
|||
16 |
4 |
6 |
|
|
|
10 |
|
26 |
|
8 |
10 |
|
|
18 |
|
36 |
|
|
32 |
3 |
9 |
44 |
|
46 |
|
|
4 |
12 |
6 |
22 |
|
56 |
|
|
|
1 |
5 |
6 |
|
nx |
4 |
14 |
46 |
16 |
20 |
N=100 |
|
Решение.
Составим корреляционную таблицу в условных вариантах, выбрав в качестве ложных нулей С1=30 и С2= 36 ( каждая из этих вариант расположена в середине соответствующего вариационного ряда).
v |
u |
nv |
|||||
-2 |
-1 |
0 |
1 |
2 |
|||
-2 |
4 |
6 |
|
|
|
10 |
|
-1 |
|
8 |
10 |
|
|
18 |
|
0 |
|
|
32 |
3 |
9 |
44 |
|
1 |
|
|
4 |
12 |
6 |
22 |
|
2 |
|
|
|
1 |
5 |
6 |
|
nu |
4 |
14 |
46 |
16 |
20 |
N=100 |
|
Найдем
Найдем вспомогательные величины
Найдем
Составим расчетную таблицу.
Пояснения к составлению таблицы.
1). Произведение частоты nuv на варианту u записывают в правом верхнем углу клетки, содержащей значение частоты.
2). Складывают все числа, помещенные в правых верхних клеток одной строки, и их сумму помещают в клетку этой же строки «столбца U».
3). Наконец, умножают варианту v на U и полученное произведение записывают в соответствующую клетку « столбца vU».
4).
Сложим все числа « столбца vU»,
получают сумму vU,
которая равна искомой сумме
.
Например, для нашей таблицы искомая
сумма
=82.
Для контроля аналогичные вычисления производят по столбцам.
Найдем искомый выборочный коэффициент
корреляции:
.
Найдем шаги h1 и h2
( разности между любыми двумя соседними
вариантами): h1=25-20=5;
h2=26-16=10/
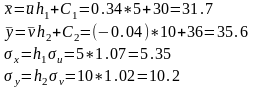
Подставив найденные величины , получим искомое уравнение прямой линии регрессии У на Х:
Задание 3. Данные наблюдений над двумерной случайной величиной (Х; Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на X .
.
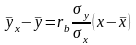1
.
Х Y |
7 |
10 |
13 |
16 |
19 |
ny |
1 |
2 |
4 |
|
|
|
6 |
3 |
|
3 |
22 |
1 |
|
26 |
5 |
|
|
6 |
7 |
|
13 |
7 |
|
|
|
3 |
2 |
5 |
nx |
2 |
7 |
28 |
11 |
2 |
n=50 |
2.
Y |
10 |
12 |
14 |
16 |
18 |
ny |
20 |
4 |
10 |
|
|
|
14 |
30 |
|
7 |
30 |
10 |
|
47 |
40 |
|
|
18 |
9 |
|
27 |
50 |
|
|
|
9 |
3 |
12 |
nx |
4 |
17 |
48 |
28 |
3 |
n=100 |
Х
3.
Y |
11 |
12 |
13 |
14 |
15 |
ny |
6 |
2 |
3 |
|
|
|
5 |
10 |
|
5 |
19 |
|
|
24 |
14 |
|
|
5 |
11 |
|
16 |
18 |
|
|
|
3 |
2 |
5 |
nx |
2 |
8 |
24 |
14 |
2 |
n=50 |
Х
4.
Y |
10 |
15 |
20 |
25 |
30 |
ny |
5 |
3 |
10 |
|
|
|
13 |
8 |
|
18 |
23 |
|
|
41 |
11 |
|
|
27 |
10 |
|
37 |
14 |
|
|
|
5 |
4 |
9 |
nx |
3 |
28 |
50 |
15 |
4 |
n=100 |
Х
5.
Y |
3 |
6 |
9 |
12 |
15 |
ny |
2 |
2 |
3 |
|
|
|
5 |
4 |
|
7 |
10 |
|
|
17 |
6 |
|
1 |
16 |
2 |
|
19 |
8 |
|
|
|
6 |
3 |
9 |
nx |
2 |
11 |
26 |
8 |
3 |
n=50 |
Х
6.
Y |
6 |
10 |
14 |
18 |
22 |
ny |
40 |
3 |
8 |
9 |
|
|
20 |
50 |
|
5 |
16 |
|
|
21 |
60 |
|
|
20 |
17 |
2 |
39 |
70 |
|
|
|
17 |
3 |
20 |
nx |
3 |
13 |
45 |
34 |
5 |
n=100 |
Х
7.
Х Y |
15 |
20 |
25 |
30 |
35 |
ny |
7 |
2 |
8 |
|
|
|
10 |
8 |
|
13 |
15 |
10 |
|
38 |
9 |
|
7 |
24 |
12 |
|
43 |
10 |
|
|
|
6 |
3 |
9 |
nx |
2 |
28 |
39 |
28 |
3 |
n=100 |
8.
Х Y |
1 |
5 |
9 |
13 |
17 |
ny |
3 |
1 |
1 |
|
|
|
2 |
6 |
|
3 |
13 |
5 |
|
21 |
9 |
|
2 |
17 |
4 |
|
23 |
12 |
|
|
|
2 |
2 |
4 |
nx |
1 |
6 |
30 |
11 |
2 |
n=50 |
9.
Y |
7 |
9 |
11 |
13 |
15 |
ny |
10 |
3 |
6 |
|
|
|
9 |
14 |
|
14 |
16 |
9 |
|
39 |
18 |
|
9 |
23 |
14 |
|
46 |
22 |
|
|
|
4 |
2 |
6 |
nx |
3 |
29 |
39 |
27 |
2 |
n=100 |
Х
10.
Х Y |
5 |
10 |
15 |
20 |
25 |
ny |
2 |
3 |
5 |
|
|
|
8 |
4 |
|
5 |
9 |
3 |
|
17 |
6 |
|
3 |
6 |
9 |
|
18 |
8 |
|
|
|
5 |
2 |
7 |
nx |
3 |
13 |
15 |
17 |
2 |
n=50 |