3.3 Поиск неисправностей авиационного оборудования.

Задача (рис. 3.6) наиболее актуальна для тех систем, в которых неисправность не определяется с точностью до съемного блока. Решение это задачи связано с построением оптимального, с точки зрения принимаемого критерия эффективности, алгоритма по­иска неисправности. Для этого необходимо выбрать оптимальный ме­тод поиска ( подзадача ) и определить минимум подозреваемых в неисправности блоков по её внешнему проявлению ( подзадача ) Причём число методов поиска значительно меньше числа возможных производственных ситуаций , а число подозреваемых блоков, как правило, меньше общего числа блоков диагностируемой системы. Поэтому необходимо использовать модели для оптимального выбора с учётом конкретной производствен­ной ситуации. Для этого на множестве методов поиска неисправнос­тей зададим бинарные отношения:

«Методы, соответствующие имеющемуся резервному времени»,

«Методы, соответствующие структуре контроля диагностируемой системы»

- «Полнота использования данных»

Тогда механизм выбора оптимального в конкретной ситуации метода с учетом последовательной организации вычислительных процессов ЛПР может быть представлен схемой:

X C C (C C (C (C

Рис.3.8. Схема выбора оптимального метода поиска неисправностей.

На множестве блоков диагностируемой системы можно задать би­нарные отношения:

–« Логически подозреваемый блок»,

- « Семантически подозреваемый блок».

Тогда механизм выбора подозреваемых в неисправности блоков по её внешнему проявлению можно представить схемой:

Рис. 3.9. Схема выбора подозреваемых в неисправности блоков.

Одним из способов улучшения выбора является принятие к рас­смотрению новых альтернатив. Анализ типовых методов поиска неис­правностей показывает, что не всегда эти методы являются опти­мальными и учитывают особенности конкретной производственной си­туации. Такой ситуацией является, например, поиск неисправности в условиях минимаксного критерия, который соответствует обнаруже­нию неисправности непосредственно перед вылетом, для систем, поз­воляющих осуществлять контроль одновременно нескольких блоков. В этом случае рекомендуется использовать метод половинного разбиения или равных вероятностей. Однако первый метод минимизирует максимальное число необходимых проверок, второй-среднее число не­обходимых проверок. В этой же ситуации рекомендуется минимизиро­вать максимальное время продолжительности работ по устранению неисправности. Следовательно, рекомендуемые методы не являются оптимальными в данной ситуаций. Для построения оптимальной стратегии поиска можно воспользоваться теоретико-игровой моделью принятия решений. Эту модель можно распространить на другие ситуации.

Во многих случаях поиск отказавшего элемента осуществляется контролем реакции диагностируемой системы в определённых точках при подаче необходимых входных воздействий. На рис. 3.10 изобра­жён участок логической схемы некоторой диагностируемой системы из N элементов. Выход - неисправен, - время контроля выхода, 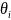- время устранения неисправности i -го блока, - возможная проверка.

Если в качестве одной стороны выбрать ЛПР, а в качестве дру­гой -природу, то процесс поиска неисправности можно представить рядом последовательно разыгрываемых игр с «природой», описываемых соответствующими платёжными матрицами. В этих играх стратегиями «природы» являются блоки возможной неисправности , а стратегиями ЛПР- отдельные проверки . Будем считать «природу» «безразличной» к выбору ЛПР. Оценку принимаемых ЛПР решений в ситуации поиска с отсутствующим резервом времени будем осуществлять по максимальным затратам на устранение неисправности , определяемым при усло­вии начала поиска с проверки и неисправности блока . В зави­симости от результата проверки R схема делится на две части. R=0 соответствует тому, что контролируемый параметр находится не в допуске, - в допуске. Предполагается при этом, что неисправен один из блоков и за время поиска новых неисправностей не. было......

Т огда, если процедура поиска начинается с проверки , а неис­правен блок , максимальные затраты складываются из суммарного времени всех проверок той части системы, где находится блок и времени устранения неисправности этого блока :

(3.11)

где , 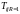- максимальные временные затраты поиска и устранения неисправности для различных частей системы, определяемые результатом проверки с учётом неисправности -го блока;

, - время отдельной проверки в одной или другой частях системы от места проведения проверки;

~ время устранения неисправности I –го блока;

- число проверок в одной части системы от места проведе­ния проверки с результатом =0;

- число всех проверок. Тогда максимально возможное время поиска и устранения неисправ­ности на основе процедуры, начинающейся с проверки , определя­ется формулой:

(3.13)

Наилучшая, с точки зрения критерия минимакса времени поиска и ус­транения неисправности, проверка, с которой следует начинать по­иск, определяется на основе формулы:

(3.14)

Эта проверка разбивает диагностируемую систему на две части, для которых решается аналогичная задача и т.д. Схема организации ал­горитма поиска на основе платёжных матриц представлена на рисун­ке 3.U. Такой алгоритм поиска неисправностей будет оптимален с точки зрения минимизации максимально возможных затрат, необходи­мых для ликвидации неисправностей, поскольку он оптимален на каж­дом шаге, а, следовательно, оптимален в целом.

-1

X

…

Рис. 3.10. Участок логической схемы диагностируемой системы

… …

1 … …

. . . .

. . . .

I … …

. . . .

. . . .

… …

R=0 R=1

… … … …

1 … … i+1 … …

. . . . . . . .

. . . . . . . .

i … … … …

. . . . . . . .

. . . . . . . .

… … … …

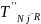Рис. 3.11. Процедура поиска неисправностей на основе платёжных матриц.