2.6. Нечёткие модели принятия решений.

Исследования в области построения автоматизированных систем организационного управления, искусственного интеллекта и роботов привели к осознанию того факта, что человеку в процессе управле­ния сложными объектами свойственно оперировать понятиями и отно­шениями с расплывчатыми (нестрогими) границами, а также выска­зываниями с многозначной шкалой истинности. При этом источником расплывчатости является существование классов объектов, степень принадлежности к которым - величина, непрерывно изменяющаяся от полной принадлежности к классу до полной непринадлежности к нему.

Введение видным американским кибернетиком Л.Заде двух основных исходных понятий - нечёткого множества и лингвистической переменной- существенно расширило возможности формализации опи­саний сложных систем.

Наиболее часто встречающиеся в задачах управления виды не­определённости можно сгруппировать в классификационное дерево (рис.2.13).

Математическим аппаратом неточности является теория размытых множеств, в которой введено понятие функции принадлежности и нечёткого множества /6/.

Пусть - произвольное непустое множество. Нечётким подмножеством множества называется множество пар

, где , (2.45)

(Например, множество "малых" чисел: М= 1/1 , 0,8/2,……,0,1/7 )

Функци называется функцией принадлежности нечёткого множества , а - базовым множеством или базовой шкалой. Для каждого конкретного значения величина принимает определённое значение из замкнутого интервала , которое называется степенью принадлежности элемента нечёткому множеству .

Нечётким высказыванием называется предложение, относительно которого можно судить о степени его истинности или ложности в настоящее время. Степень истинности или степень ложности каждого нечёткого высказывания принимает значения из замкнутого интервала , причём 0 и 1 являются предельными значениями степени истинности и совпадают с понятиями лжи и истины для "чётких" высказываний.

Отрицанием нечёткого высказывания называется нечёткое высказывание, обозначаемое степень истинности которого оп­ределяется выражением:

(2.46)

Конъюнкцией нечётких высказываний называется нечёткое высказывание, обозначаемое ,степень истинности которого определяется следующим образом:

(2.47)

Дизъюнкцией нечётких высказываний , называется нечёткое высказывание, обозначаемое степень истинности которого определяется как:

(2.48)

Импликацией нечётких высказываний называется нечёткое высказывание, обозначаемое , степень истинности которого определяется выражением

(2.49)

(2.49)

Эквивалентностью нечётких высказываний называется нечёткое высказывание, обозначаемое , степень истинности которого находится как:

(2.50)

Нетрудно убедиться, что данные выше определения в случае, когда степень истинности высказываний и принимает только два значения: 0 и 1,соответствуют определениям логических операций над чёткими высказываниями.

Таким образом, нечёткое множество состоит из некоторого множества нечётких высказываний.

Под нечёткой высказывательной переменной будем понимать чёткое высказывание, степень истинности которого может принимать произвольные значения из замкнутого интервала

Над нечёткими множествами могут производиться операции! единения, пересечения, дополнения и др. Особое значение в системах принятия решений имеют нечёткое включение и нечёткое равенство множеств.

Пусть заданы нечёткие подмножества и множества X . Введём понятие степени включения нечёткого множества нечёткое множество , которая находится по формуле

(2.51)

где , понимаются как нечёткие высказывательные переменные, операция импликации нечётких высказываний, а - операция конъюнкции, которая берётся по всем . Естественно, аналогичным образом можно определить и степень включения нечеткого множества в множество .

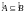Если , то будем полагать, что множество нечётко включается в множество , и обозначать . Если , то будем считать, что множество нечётко не включается в множество , и обозначать Легко видеть, что рассмотренное понятие нечёткого включения нечётких множеств является обобщением понятия включения чётких множеств. Действительно, если и - чёткие множества и , , а в случае если , величина

Пример 2.1. Пусть, ,

Тогда

Таким образом, а

Степень равенства нечётких множеств и определяется выражением

(2.52)

где « » - операция эквивалентности нечётких высказываний, а «&»- операция конъюнкции по всем .

Если , то будем полагать, что множества и нечётко равны, и обозначать. Если, то будем считать что множества и нечётко не равны, и обозначать. В случае, когда =0,5, множества взаимно индифферентны ( ).

Пример2.2.Пусть

.Тогда

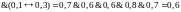
Т.о. 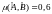и

Нечёткой переменной будем называть , где -наименование нечёткой переменной, Х={x} -область её определения (базовое множество), -нечёткое подмножество множества , описывающее ограничения на возможные значения нечёткой -переменной .

Лингвистической переменной будем называть тройку где - название лингвистической переменной, - терм-множество лингвистической переменной , т.е. множество лингвистических значений переменной, причём каждое из этих значений является нечёткой переменной с областью определения .

Пример 2.3. Пусть оценивается стоимость выполнения некоторых работ по обслуживанию авиационной техники с помощью понятий "малая", "средняя", "высокая". Стоимость, в зависимости от вида работ, может изменяться от 100 до 5000 ед. Формализация такого описания может быть проведена при помощи лингвистической переменной <"Стоимость", , [100,5000] >,где = {"малая", "средняя", "высокая"}.Значения лингвистической переменной "Стоимость" терм-множества описываются нечёткими переменными с соответствующими наименованиями и ограничениями на возможные значения, пример, значение "малая" задаётся нечёткой переменной < "малая [100,5000], > ,где нечёткое множество может быть следующим:

Примерный вид непрерывных функций принадлежности нечётких множеств, описывающих значения лингвистической переменной «Стоимость» приведён на рис. 2.14.

Функции принадлежности могут строиться с помощью экспертныхоценок, выбираться из набора эталонных функций.

Лингвистические переменные играют важную роль при построе­нии нечётких моделей принятия решений.

Во многих случаях при построении нечётких моделей принятия решений эффективным является вывод ситуационного типа.

Дадим теперь формальное определение "нечёткой" ситуации.

Пусть -множество признаков, значениями

_{которых} описываются состояния объекта управления. Каждый признак описывается соответствующей лингвистической переменной , где - терм-множество лингвистической переменной ( набор лингвистических значений признака, - число значений признака); – базовое множество признака . Для описания термов соответствующих значениям признака , используются нечёткие переменные - значение описывается нечётким множеством в базовом множестве

Нечёткой ситуацией называется нечёткое множество

(2.54)

где

(2.55)

Пример 2.4 характеризует некоторое состояние объекта диагности­рования на основе ситуационного подхода.

Пример 2.4 , , Значение амплитуды контролируемого сигнала" > , , "Значение частоты контролируемого сигнала">} .

Для определения состояния объекта управления необходимо сравнить входную нечёткую ситуацию с каждой нечёткой ситуацией из некоторого набора типовых нечётких ситуаций, решения для ко' рых известны. В качестве меры для определения степени близости нечётких ситуаций могут использоваться степень нечёткого включения ситуаций, степень нечёткого равенства, степень нечёткой об­щности, а также другие меры близости. Выбор меры близости определяется особенностями объекта управления и организацией процесса принятия решения.

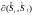Степень включения ситуации в ситуацию обозначается определяется выражением

(2.56)

Пример 2.5. Пусть , ,

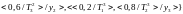.Тогда

.

Следовательно

Нечёткое равенство ситуаций определяется выражением

(2.57)

_{Пример 2.6. Пусть}

_Тогда

Ситуации и нечётко равны при пороге t= 0,7.

Нечёткой -общностью ситуаций назовём такое сходство ситуаций, когда нечёткие значения всех признаков в ситуациях нечётко равны, кроме нечётких значений не более, чем признаков. Если ситуации и описываются признаками, то для их - общности достаточно нечёткого равенства признаков из множества .

Степень - общности ситуаций и определяется выражением

где , признак принадлежит , если

Одна ситуация включается в другую, две ситуации нечётко рав­ны или обладают - общностью, если соответствующие степени не меньше некоторого порога . Обычно .

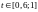Пример 2.7. Определить степень - общности, если

Ситуации

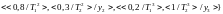
имеют 2-общность при =0,7, так как

Следовательно,