- •2.3. Модели принятия решений на основе функций полезности.
- •2.4 . Теоретико-игровые модели принятия решений.
- •2.5. Марковские модели принятия решений.
- •2.6. Нечёткие модели принятия решений.
- •2.7. Байесовский метод принятия решений.
- •3. Применение моделей принятия решений в задачах технической эксплуатации авиационного оборудования.
- •3.1. Оценка технического состояния авиационного оборудования.
- •3.2. Восстановление авиационного оборудования.
- •3.3 Поиск неисправностей авиационного оборудования.
- •4. Совершенствование процессов принятия решений.
- •4.1. Автоматизация процессов принятия решений.
- •4.2. Тренировка процессов принятия решений.
Таблица 2.1. Пример функций выбора на двухэлементном множестве.
№ |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
0 |
|
|
5 |
|
0 |
|
Не существует |
Не существует |
6 |
0 |
|
|
Не существует |
Не существует |
7 |
|
0 |
|
|
|
8 |
|
0 |
|
Не существует |
Не существует |
9 |
0 |
|
|
|
|
10 |
0 |
|
|
Не существует |
Не существует |
11 |
|
0 |
0 |
|
|
12 |
0 |
|
0 |
|
|
13 |
0 |
0 |
|
Не существует |
Не существует |
14 |
0 |
0 |
|
Не существует |
Не существует |
15 |
0 |
0 |
|
Не существует |
Не существует |
16 |
0 |
0 |
0 |
|
|
111Equation Chapter 1 Section 1
Приведенные примеры показывают, что не для всех функций выбора существуют бинарные отношения. Это важно учитывать при разработке моделей принятия решений. В этом случае возникает задача аппроксимации функции выбора, т.е. наилучшего ( в условном смысле ) приближения реализуемой функции. При этом выбор, при котором для некоторых из присутствующих вариантов неизвестно, должны они быть приняты или отвергнуты, называется "неполным".
Один из наиболее распространённых способов выбора на основе нескольких отношений состоит в построении по ним некоторого нового отношения и выбора по этому отношению. Такая процедура называется выбором по агрегированному отношению. На основе выбора по агрегированному отношению строятся многие механизмы. Укажем некоторые из них.
а) Выбор по Парето:
CP
(X) =
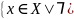 X)
yPx}
X)
yPx}
где Р - отношение Парето, задаваемое выражением:
 (2.12)
(2.12)
Где
xj,
yj
- оценки альтернатив x
и y
по критерию j.
Множеством Парето
 называется
множество:
называется
множество:
 (2.13)
(2.13)
б) Лексикографический выбор учитывает важность критериев:
 (2.14)
(2.14)
в) Мажоритарный выбор соответствует модели с равноценными критериями. Вариант x "предпочитается" варианту y , если х превосходит y по большему числу критериев, чем у превосходит x:
 (2.15)
(2.15)
г) Совокупно – экстремальный выбор. Выбираются варианты, являющиеся лучшими хотя бы по одному из критериев:
 (2.16)
(2.16)
д)
Выбор на основе метода идеальной точки
связан с введением- - максимального назначения по i
-ому
критерию. Тогда точка
- максимального назначения по i
-ому
критерию. Тогда точка идеальная. Смысл названия связан с тем,
что такие точки оптимальны сразу по
всем критериям: получить большее
значение ни по одному критерию невозможно.
При этом альтернативы удобно
изображать точками в пространстве
критериев. Как правило, идеальная
точка
идеальная. Смысл названия связан с тем,
что такие точки оптимальны сразу по
всем критериям: получить большее
значение ни по одному критерию невозможно.
При этом альтернативы удобно
изображать точками в пространстве
критериев. Как правило, идеальная
точка
 не
принадлежит
не
принадлежит

Зададим
для всех альтернатив функцию, являющуюся
расстоянием между альтернативами
и
 :
:
 (2.17)
(2.17)
Решением
(рис.2.5) является альтернатива
 ,
для которой
,
для которой
 (2.18)
(2.18)

В реальной практике широко распространён способ, когда итоговая функция выбора формируется некоторым способом из функций выбора по отдельным отношениям.
Модель последовательного выбора учитывает упорядочивание целей по важности:
 (2.19)
(2.19)
Схема последовательного выбора представлена на рис.2.6
...
Rk
R1
X




Рис. 2.6. Схема последовательного выбора.
Множество вариантов в схеме последовательного выбора постепенно сужается при переходе к выбору по очередному отношению. С таким типом выбора встречаются, когда ЛПР каким-либо способом упорядочивает свои цели по важности, либо когда в принятии решения участвуют несколько лиц, не равных по служебной иерархии. Сюда относятся случаи, когда сверху даётся некоторая директива, которая при продвижении вниз последовательно уточняется, либо, наоборот, когда решение готовится на нижнем уровне, и предлагаются несколько вариантов, а окончательно оно принимается на более высоком уровне.
Параллельный выбор осуществляется независимо по нескольким отношениям:
 (2.20)
(2.20)
где
 -
функция агрегирования, являющаяся
пересечением или объединением множеств
вариантов, выбираемых по отдельным
отношениям.
-
функция агрегирования, являющаяся
пересечением или объединением множеств
вариантов, выбираемых по отдельным
отношениям.
В этой модели каждый участник производит независимо от других выбор по некоторому отношению, затем на этой основе формируется окончательный выбор. Такая ситуация возникает, когда решение готовится параллельно несколькими людьми, а затем их мнения совмещаются каким-либо образом в итоговом решении. Этой моделью описываются некоторые экспертные процедуры.
Схема параллельного выбора представлена на рис. 2.7.
X

F

 .
. 

 .
.
Rk
X 
Рис. 2.7.Схема параллельного выбора.
Механизм последовательно-параллельного выбора формируется следующим образом:
 (2.21)
(2.21)
Схема, последовательно-параллельного выбора представлена на рис. 2.8.


Х
 .
. . F
.
. . F
.
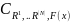

.
X
 .
. .
.
. .
Рис. 2.8.Схема последовательно-параллельного выбора.
Эта модель соответствует процедуре с участием нескольких лиц, в которой каждый участник независимо производит последовательный выбор в соответствии с некоторой иерархией своих целей, а затем их мнения «совмещаются» в одно.
Многие модели принятия решений, использующие язык критериев, охватываются традиционной схемой математического программирования:
 (2.22)
(2.22)
где
 ,
, - скалярные
функции векторного аргумента;
- скалярные
функции векторного аргумента;
 -
фиксированные
скаляры.
-
фиксированные
скаляры.
Вычислительные схемы математического программирования могут быть обобщены и использованы в качестве механизмов выбора решений в ситуациях, описываемых на языке бинарных отношений. При этом возникает задача обобщённого математического программирования:
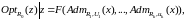 (2.23)
(2.23)
где
 (2.24)
(2.24)
 (2.25)
(2.25)
 –
множество
эталонных вариантов,
–
множество
эталонных вариантов,
 –
множество
допустимых вариантов.
–
множество
допустимых вариантов.
Схема задачи обобщённого математического программирования (ОМП) представлена на рис.2.9.

R0
. F C(x).

Рис. 2.9.Схема задачи ОМП.
Многие
процедуры принятия решений имеют
иерархическую структуру, их
формализация приводит к многошаговым
задачам обобщённой математического
программирования (МнОМП).
Многошаговая задача разбивается на
 последовательно
решаемых задач, относящихся к шагам
последовательно
решаемых задач, относящихся к шагам
 :
:
 (2.26)
(2.26)
где
 -
результат
шага
-
результат
шага -
предъявление.
-
предъявление.
Решением
задачи является
 .
.
На рис. 2.10 показана двухшаговая схема общего вида.
x

.

.
 F(1)
x(1) .
F(1)
x(1) .
. .
x .
x
 (2)
(2)
x
. .
. .
. .
x
Рис. 2.10. Двухшаговая схема задачи МнОМП.
Модели последовательного, параллельного, последовательно – параллельного типов являются частными случаями задачи МнОМП.
2.3. Модели принятия решений на основе функций полезности.
Очень
часто принятие решений осуществляется
на основе анализа последствий от
выбора альтернатив /4/. Схема, такого
выбора из двух альтернатив
 и
и
 представлена на рис. 2.11.
представлена на рис. 2.11.
|
|
Рис. 2.11. Схема выбора на основе функции полезности.
Каждому последствию ставится в соответствие некоторая величина, задающая функцию полезности на множестве последствий. При этом
(
предпочтительнее
)
<=>
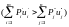 ,
(2.27)
,
(2.27)
 -
называется ожидаемой полезностью;
-
называется ожидаемой полезностью;
 вероятность
появления
вероятность
появления
 -
го последствия;
-
го последствия;
 .
.
Если
полезность последствия оценивается с
учётом
 факторов
факторов
 ,
она может быть представлена в виде:
,
она может быть представлена в виде:
где
 - положительные шкалирующие константы.
- положительные шкалирующие константы.
В некоторых условиях можно обойтись более простыми способами и не прибегать к максимизации ожидаемой полезности.
Предположим,
что возможные последствия альтернатив
 и
и
 описываются
функциями распределения вероятностей,
представленными на рис. 2.12. Критерий,
используемый для оценки результатов,
обозначим через
описываются
функциями распределения вероятностей,
представленными на рис. 2.12. Критерий,
используемый для оценки результатов,
обозначим через

 Рис.
2.12.Иллюстрация доминирования по
вероятности.
Рис.
2.12.Иллюстрация доминирования по
вероятности.
Из
рис. 2.12 видно, что вероятность того, что
исход будет не более
,
у альтернативы
больше,
чем у альтернативы
.Следовательно,
если большие значения
предпочтительнее
меньших, то
предпочтительнее,
чем
 доминирует
по вероятности над
.
доминирует
по вероятности над
.
2.4 . Теоретико-игровые модели принятия решений.
В общем случае игра сторон может быть задана в виде множества:
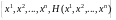 (2.29)
(2.29)
где
 - платёж игры, который, в частности,
может быть задан в виде матрицы;
- платёж игры, который, в частности,
может быть задан в виде матрицы;
 -
множество стратегий
-й
стороны;
-
множество стратегий
-й
стороны;
 -
число играющих сторон.
-
число играющих сторон.
Мы будем рассматривать антагонистические и неантагонистические статические и динамические игры двух сторон с нулевой суммой когда выигрыш одной стороны равен проигрышу другой /5/.
Такая игра может быть представлена матрицей:
Стратегии 1-го игрок

 -доход
игрока 1 при выборе им
-й
стратегии и выборе
-доход
игрока 1 при выборе им
-й
стратегии и выборе
 -й
игроком 2.
-й
игроком 2.
Наилучшая
стратегия игрока 1 выбирается из условия
выбора игроком 2 "худших" для игрока
1 стратегий. Очевидно, 1. выберет такую
стратегию, при которой будет максимальным
значение минимумов по строкам
 .
.
Аналогично
рассуждает и игрок 2. Тогда его стратегия

Условие, удовлетворяющее обе стороны
 (2.30)
(2.30)
Значения
и
,
при которых
 называются решением игры и образуют
седловую точку. Величина
называются решением игры и образуют
седловую точку. Величина
 называется
ценой игры.
называется
ценой игры.
Седловая точка может отсутствовать. В этом случае говорят об оптимальных значениях вероятности появления каждой стратегии. Обозначим через:
 (2.31)
(2.31)
матрицу - столбец, состоящую из вероятностей , выбора -й стратегии 1-го игрока, и через
 (2.32)
(2.32)
соответственно матрицу- столбец ( вектор ) вероятностей появления стратегий 2-го игрока.
Тогда средний платёж 1-го игрока:
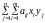 (2.33)
(2.33)
Основная теорема теории игр, теорема о минимакcе, утверждает, что максимин среднего платежа равен минимаксу среднего платежа, т.е.
 (2.34)
(2.34)
Одним из методов решения этой задачи является метод линейного программирования.
В задачах игр с "природой" она является одним из игроков, " безразличной" к выбору стратегий другой стороны ( ЛПР ).