1. Перечислительная комбинаторика.

1. Сколько можно образовать трёхзначных чисел, состоящих из различных цифр?

Решение. Из 10 цифр: 0, 1, 2, 3, 4, 5, ,6, 7, 8 ,9 можно составить число размещений по 3: 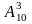= 1098=720. Но из этого числа надо исключить число тех размещений по 3, которые начинаются с цифры 0. Таких размещений будет столько, сколько можно составить размещений из 9 цифр по 2:

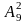=98=72. Искомое число равно 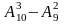=720–72=648.

Ответ: 648.

2. Сколькими способами можно разместить 12 лиц за столом, на котором поставлено 12 приборов?

Решение. Это будет число перестановок из 12

Р₁₂=12!=123 … 12=479001600.

Ответ: 479001600.

3. Бригадир должен отправить на работу бригаду из 5 человек. Сколько бригад по 5 человек в каждой можно составить из 12 человек?

Решение. Таких бригад будет столько, сколько будет сочетаний из 12 элементов по 5, то есть:

.

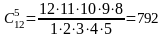Ответ: 792.

Задачи для самостоятельного решения

1. Сколько различных 4-х значных чисел, делящихся на 4 можно составить из цифр 1, 2, 3, 4, 5, если цифры могут повторяться?

2. Сколькими способами можно переставить буквы слова «ЛОГАРИФМ» так, чтобы 2-е, 4-е и 6-е места были заняты согласными буквами?

3. Сколько нечётных чисел можно составить из цифр числа 53694 (каждую цифру можно использовать не более одного раза)?

4. Сколькими способами 15 одинаковых подарков можно раздать 7 детям, если каждый ребёнок должен получить хотя бы один подарок?

5. Переплётчик должен переплести 12 различных книг в красный, зелёный и коричневый переплёты. Сколькими способами он может это сделать, если в каждый цвет должна быть переплетена хотя бы одна книга?

6. Сколько неотрицательных целых чисел меньше, чем 10 миллионов содержат цифры 2, 3, 4, 5, 6? Сколько чисел состоит только из этих цифр?

7. Сколько имеется шестизначных чисел, у которых 3 цифры – чётные, а 3 – нечётные? Сколько из этих чисел чётных?

8. Множество A состоит из n различных элементов. Сколькими способами можно переставить элементы этого множества, чтобы два фиксированных элемента a и b не стояли рядом? Никакие два элемента, из элементов a, b, c не стояли рядом?

9. Сколько четырехзначных чисел можно образовать из цифр 0; 1; 2; 3? (Цифры в числе не должны повторяться).

10. Сколько прямых линий можно провести через 8 точек, из которых никакие три не лежат на одной прямой?

11. Сколькими способами можно написать различные пятизначные числа при помощи цифр 1, 2, 3, 4, 5, 6, 7, 8, 9? (Цифры не повторяются).

12. Сколько всевозможных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7? (Цифры не повторяются).

13. Из 10 девушек и 8 юношей нужно составить бригаду, состоящую из двух девушек и трех юношей. Сколько можно составить различных бригад?

2. Определения вероятности

1. В ящике 300 деталей. Известно, что 150 из них 1 сорта, 120 – 2-го сорта, а остальные – 3-го сорта. Определить вероятность, что наугад взятая деталь будет: а) 3-го сорта; б) 1 или 2 сорта.

Решение. Опыт состоит в выборе на удачу одной детали. Общее число исходов n=300. Обозначим через событие А – деталь 3-го сорта, через событие В – деталь 1 или 2 сорта. Число благоприятствующих событию А исходов m=30. Тогда:

.

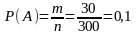а) Среди 300 деталей 300–150–120=30 деталей 3-го сорта.

б) Событию В благоприятствует m=150+120=270 исходов, откуда:

.

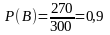Ответ: 0,1; 0,9.

2. По списку в группе 25 студентов. Каждый второй из них по списку получает билет на выставку, а каждый третий – билет в кино. Какова вероятность случайно взятому студенту получить сразу два билета, если неизвестно, на каком месте по списку расположена его фамилия?

Решение. Каждый второй по списку соответствует порядковому номеру, кратному двум, а каждый третий – порядковому номеру, кратному трем. Чтобы получить два билета надо находиться по списку на месте, порядковый номер которого является кратным и двум и трем, то есть – шести.

Среди 25 чисел кратным шести являются четыре числа: 6, 12, 18, 24. Следовательно, число благоприятных исходов m=4, а число всех возможных исходов n=25. Тогда искомая вероятность равна:

.

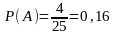Ответ: 0,16.

3. Среди 20 экзаменационных билетов 5 содержат легкие вопросы. Определить вероятность:

а) первому экзаменующемуся вытянуть легкий билет (событие А);

б) первым четырем экзаменующимся не вытянуть ни одного легкого билета (событие В).

Решение.

а) Число всех возможных исходов равно количеству билетов, т.е. n=20. Число исходов благоприятствующих событию А равно количеству легких билетов, т.е. m=5. Тогда

.

б) Число всех исходов равно числу способов выбрать 4 билета из 20, т.е. числу сочетаний из 20 по 4:

.

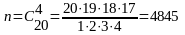Так как порядок извлечения четырех билетов не важен, то число исходов, благоприятствующих событию В равно числу способов выбрать 4 “трудных” билета из 15, т.е. числу сочетаний из 15 по 4, а именно

.

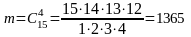Следовательно,

.

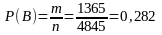Ответ: 0,25; 0,282.

4. По телевидению передано 10 снимков, из них 3 снимка с искажениями. Какова вероятность, что два взятых наудачу снимка: а) не имеют искажений; б) оба имеют искажения; в) один имеет искажения?

Решение. Учитывая, что число всех возможных исходов равно числу сочетаний из 10 по 2, т.е.

.

Обозначим события:

а) Событие А – оба снимка не имеют искажения, т.е. они выбраны из 7 качественных снимков. Тогда число исходов, благоприятствующих событию А равно числу сочетаний из 7 по 2, т.е.

.

б) Событие В – оба снимка имеют искажения, т.е. они взяты из трех не качественных. Тогда число исходов, благоприятствующих событию В равно числу сочетаний из 3 по 2, т.е.

.

в) Событие С – один имеет искажение, а один не имеет искажения, т.е. один снимок взят из 3, а один взят из 7. По правилу произведения это можно сделать m=37=21 способами.

Тогда .

Ответ: 0,467; 0,067; 0,467.

5. В коробке находятся 6 красных и 4 синих карандаша. Какова вероятность того, что два карандаша, взятых наудачу окажутся одного цвета (событие А)?

Решение. Число возможных исходов – это число сочетаний из 10 по 2:

.

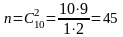Два карандаша синего цвета можно взять числом сочетаний из 4 по 2:

,

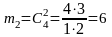а два карандаша красного цвета – число сочетаний из 6 по 2:

.

Общее число вариантов – взять два карандаша одного цвета, по правилу суммы, равно m=m₁+m₂=15+6=21.Тогда

.

Ответ: 0,467.

6. На предприятии работают 8 слесарей, из которых 3 – высокой квалификации и 5 токарей, из которых 2 – высокой квалификации. В командировку надо отправить группу из 3 слесарей и 2 токарей. Какова вероятность того, что в этой группе окажется, по крайней мере, 1 слесарь высокой квалификации и, по крайней мере, 1 токарь высокой квалификации, если каждый рабочий имеет равные возможности поехать в командировку?

Решение. В группу командированных нужно выбрать 3 слесарей из 8. Имеем 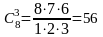вариантов такого выбора. Аналогично, из 5 токарей послать в командировку 2 можно 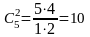различными способами. Так как любые три слесаря могут поехать с любыми двумя токарями, то число возможных исходов по правилу произведения будет равно

.

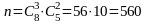Найдем число исходов. Различных групп по 3 из 5 слесарей невысокой квалификации можно составить 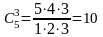. А тогда, число групп, содержащих хотя бы одного слесаря высокой квалификации будет равно . Аналогично рассуждая мы получим, что число групп по 2 токаря, содержащих хотя бы одного токаря высокой квалификации, будет равно . Учитывая, что любая из 46 групп слесарей может сочетаться с любой из 7 групп токарей, то по правилу произведения, число благоприятных групп будет равно . 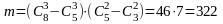Искомая вероятность будет равна

.

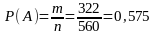Ответ: 0,575.

7. В лесном массиве площадью 50 км², где запланировано строительство Дома отдыха, находится источник минеральной воды. Какова вероятность того, что он окажется на территории, намеченной для Дома отдыха, имеющей форму круга с радиусом R=l км, если нахождение его в любой точке леса равнoвозможно?

Решение. Источник воды будем рассматривать как точку по сравнению с площадью леса и Дома отдыха. Используя геометрическое определение вероятности, найдем искомую вероятность, как отношение площади Дома отдыха к площади лесного массива, т.е.

.

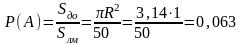Ответ: 0,063.