Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Комсомольский-на-Амуре государственный

технический университет»

Факультет электротехнический

Кафедра ЭПАПУ

Курсовая работа

по дисциплине «Теория автоматического управления»

Анализ и синтез систем автоматического управления

(линейной и нелинейной системы).

Вариант – 2

Студент группы 9ЭП-1 А. А. Калинин

Преподаватель Г.М. Гринфельд

2012

Содержание

1 Расчёт линейной системы автоматического управления …………….……..3

2 Расчёт нелинейной системы автоматического управления.………….……17

3 Литература ………….……………….……………….……………….………21

Р асчет линейной системы автоматического управления

Рисунок 1 – Исходная структурная схема линейной САУ

1. Проанализировать устойчивость замкнутой сис­темы, используя прямой метод оценки устойчивости и произвольно выбранный критерий устойчивости.

Исходные данные:

Передаточная функция разомкнутой САУ по входному сигналу:

Передаточная функция замкнутой САУ по входному сигналу:

Оценка устойчивости САУ прямым методом

Определим полюса передаточной функции замкнутой САУ:

Характеристическое уравнение:

Вещественные части всех корней характеристического уравнения отрицательные, следовательно, замкнутая САУ устойчивая.

Оценка устойчивости САУ с помощью определителя Гурвица:

Все коэффициенты характеристического уравнения - положительны, то есть необходимое условие выполняется.

Заполняем определитель:

Находим диагональные миноры:

Диагональные миноры положительны – система устойчива.

2. Провести синтез последовательного и параллельного корректирующих звеньев, обеспечивающих следующие показа­тели качества процесса регулирования в скорректированной системе:

a) перерегулирование σ ≤ 25 %;

б) длительность переходного процесса, не превышающую значения

t_рег=0.4с

в) установившаяся ошибка по скорости скорректированной системы не превышает в 0,5 раза ошибки по скорости нескорректированной системы.

Последовательная коррекция

Определим по номограмме (рисунок 3) частоту среза для данных показателей качества:

;

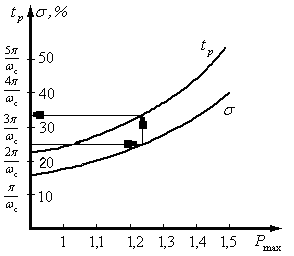
Рисунок 2 – Номограмма для определения частоты среза желаемой ЛАХ.

Т. к. длительность переходного процесса не должна превышать значения

t_рег=0.4с, пусть t_р=0.4с. Тогда:

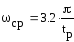
Коэффициент усиления нескорректированной системы:

Установившаяся ошибка по скорости нескорректированной системы:

Установившаяся ошибка по скорости скорректированной системы:

Коэффициент усиления скорректированной системы:

;

Передаточная функция разомкнутой нескорректированной системы:

ЛАХ нескорректированной САУ:

Для обеспечения в максимальной степени запаса устойчивости по фазе возьмем ЛАХ желаемой САУ соответственной ЛАХ типа D:

+

+

=>

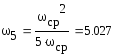
T₅=0.2

Передаточная функция желаемой САУ:

ЛАХ корректирующего звена:

Передаточная функция корректирующего звена:

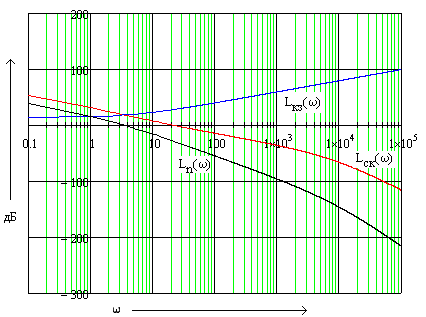
Рисунок 3 – ЛАХ нескорректированной и скорректированной систем и корректирующего звена.

Смоделируем коррекцию САУ в MATLAB

Рисунок 4 – Последовательная коррекция САУ смоделированная в MATLAB

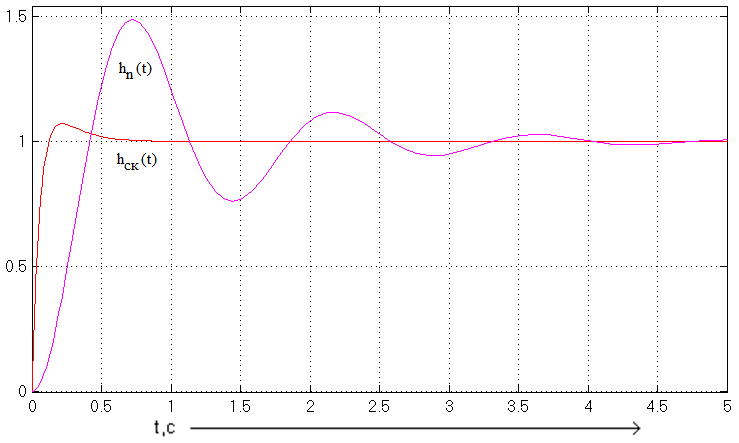
Рисунок 5 – Переходные функции нескорректированной и скорректированной системы.

По рисунку 5 определим:

Перерегулирование в скорректированной системе:

Длительность переходного процесса (время регулирования) в скорректированной системе:

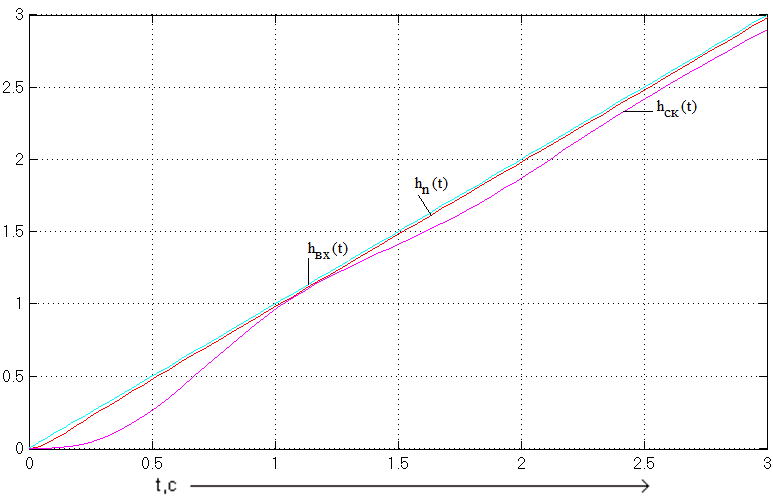
Рисунок 6 – Реакции скорректированной и нескорректированной систем на равномерно нарастающий сигнал.

По рисунку 6 определим установившуюся ошибку по скорости в скорректированной системе:

Параллельная коррекция

Передаточная функция разомкнутой нескорректированной системы:

ЛАХ нескорректированной САУ:

+

+

Передаточная функция желаемой САУ:

ЛАХ желаемой САУ:

Передаточная функция охватываемого звена САУ:

ЛАХ охватываемого звена САУ:

Передаточная функция корректирующего звена:

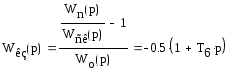
ЛАХ корректирующего звена:

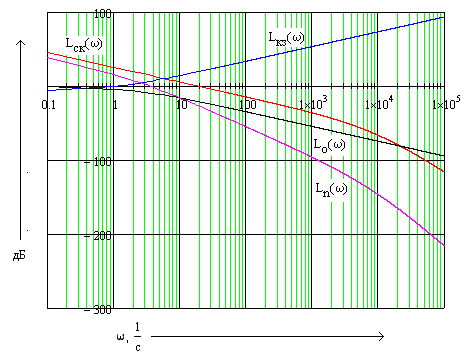
Рисунок 7 – ЛАХ нескорректированной и скорректированной систем, и ЛАХ корректирующего и охватываемого звеньев

Смоделируем коррекцию САУ в MATLAB, добавив дополнительное пос­ледовательное корректирующее звено.

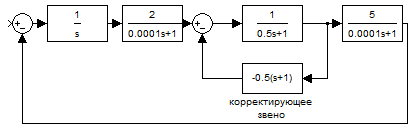
Рисунок 8 – Параллельная коррекция САУ смоделированная в MATLAB

Рисунок 9 – Переходные функции нескорректированной и скорректированной системы.

По рисунку 9 определим:

Перерегулирование в скорректированной системе:

Длительность переходного процесса (время регулирования) в скорректированной системе:

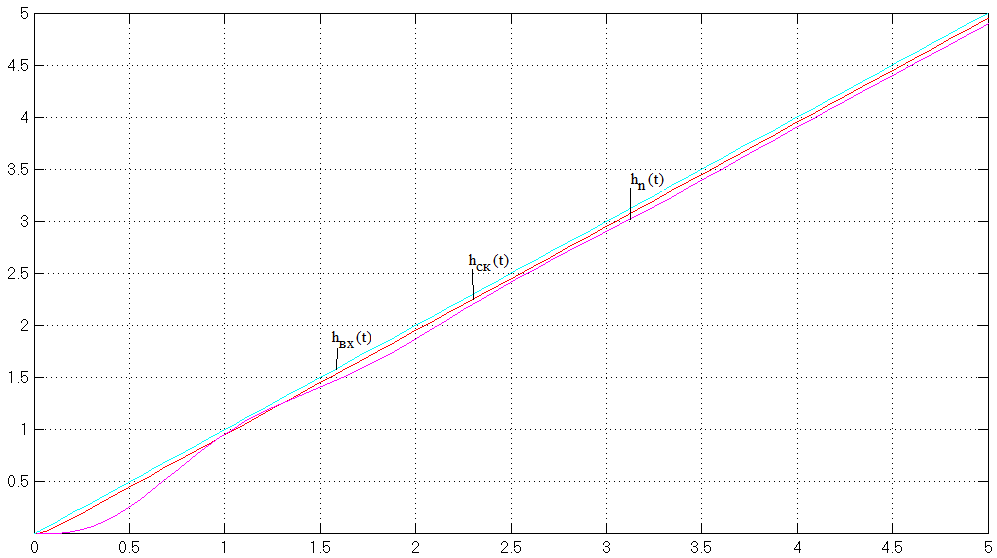
Рисунок 10 – Реакция системы на равномерно нарастающий сигнал

нескорректированной и скорректированной систем.

По рисунку 10 определим установившуюся ошибку по скорости в скорректированной системе:

3. Описать систему в пространстве состояния.

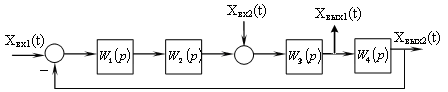
Рисунок 11 – Структурная схема нескорректированной САУ.

Метод прямого программирования:

Составим детализованную структурную схему:

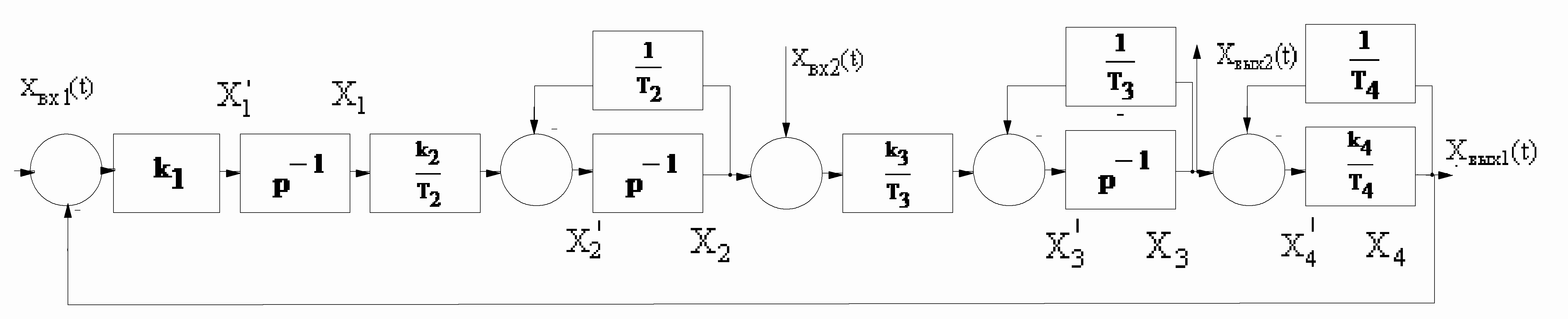
Рисунок 12 – Детализованная структурная схема.

Система дифференциальных уравнений, описывающих динамику линейной САУ:

;

;

;

;

Уравнения связи выходных сигналов с переменными состояния:

;

;

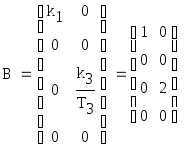
Введем в рассмотрение матрицу системы (коэффициентов системы) – А, матрицу входов (управления) – В и матрицу выхода (наблюдения) – С:

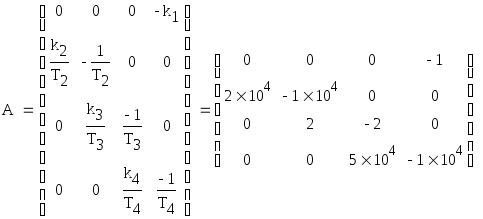
Запишем матричную передаточную функцию замкнутой системы при нулевых начальных условиях:

, где 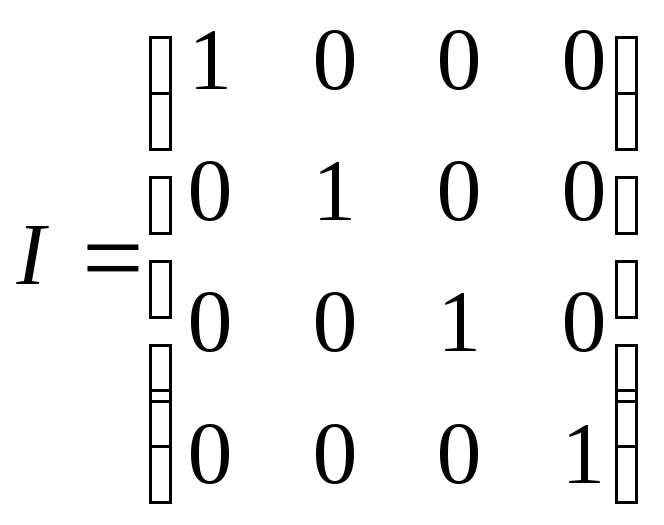- единичная матрица

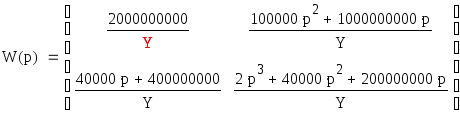
,где

Матрица переходов описывается выражением:

Выполнив обратное преобразование Лапласа от матрицы , получим фундаментальную матрицу системы.

Переменные состояния определяются выражением:

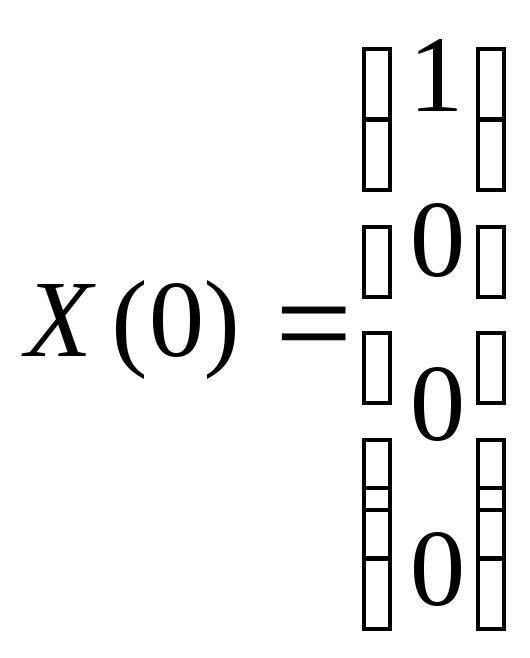, где – вектор начальных условий

Найдем аналитическое выражение для , используя теорему Сильвестра

Характеристическое уравнение:

Корни этого уравнения:

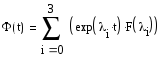
По теореме Сильвестра, матрица перехода представима в виде:

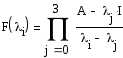г де

Запишем формулы всех

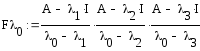
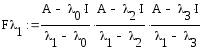
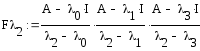
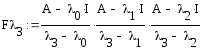
Таким образом матрица перехода представлена в виде:

Переменные состояния:

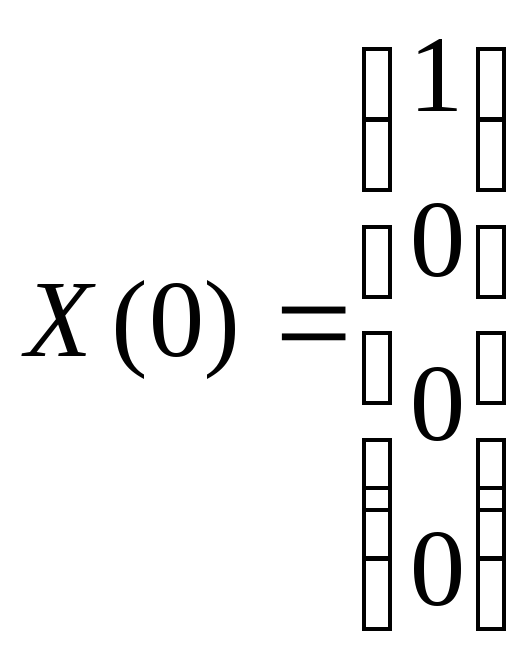, где – вектор начальных условий

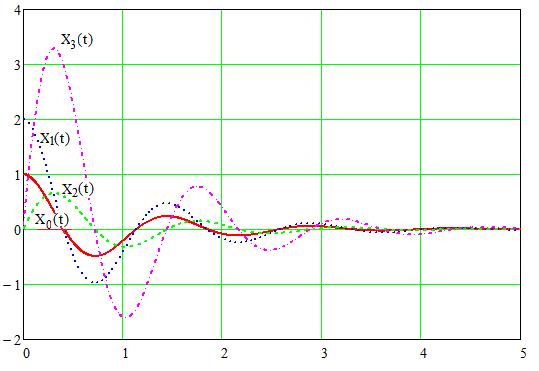
Рисунок 13 – Графики переменных состояния.

Смоделируем детализованную систему в MATLAB:

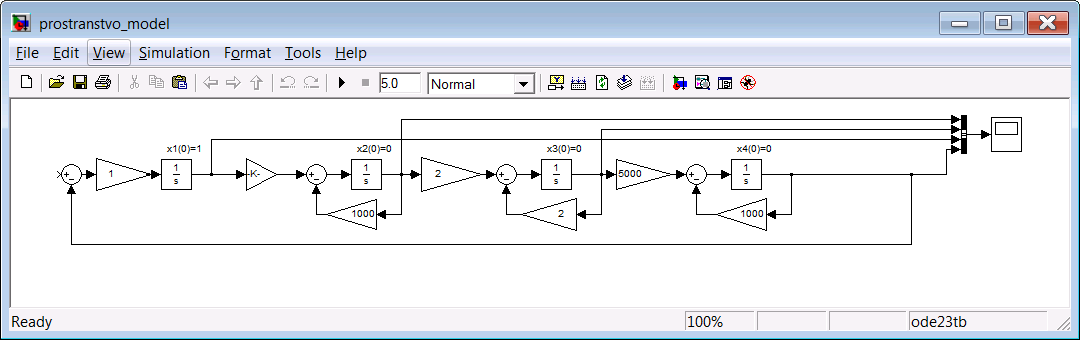
Рисунок 14 – Нескорректированная САУ, смоделированная в MATLAB

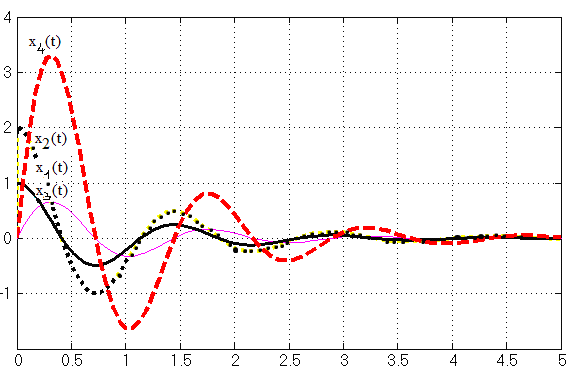
Рисунок 15 – Графики переменных состояния

системы смоделированной в MATLAB

4. Рассчитать точность скорректированной системы по управляющему и возмущающему воздействиям в установившемся режиме.

Запишем передаточные функции скорректированной разомкнутой и замкнутой систем, а также функции по ошибке и возмущающему воздействию. Рассчитаем точность системы по управляющему и возмущающему воздействию.

Передаточная функция разомкнутой скорректированной САУ по входному сигналу:

Передаточная функция замкнутой скорректированной САУ по входному сигналу:

Передаточная функция замкнутой скорректированной САУ по ошибке:

Так как передаточная функция имеет нулевой полюс, то система – астатическая с астатизмом первого порядка.

Коэффициенты ошибки системы:

; (т.к. порядок астатизма = 1) – ошибка по положению.

- ошибка по скорости.

Передаточная функция разомкнутой скорректированной системы по возмущающему сигналу:

Передаточная функция замкнутой скорректированной системы по возмущающему сигналу:

5. Определить критическое время запаздывания, при котором скорректированная система будет находиться на границе устойчивости.

Для САУ после последовательной коррекции:

Значение фазочастотной характеристики на частоте среза (рисунок 16), тогда запас по фазе:

Критическое время запаздывания:

Критическая частота: ; тогда запас по амплитуде:

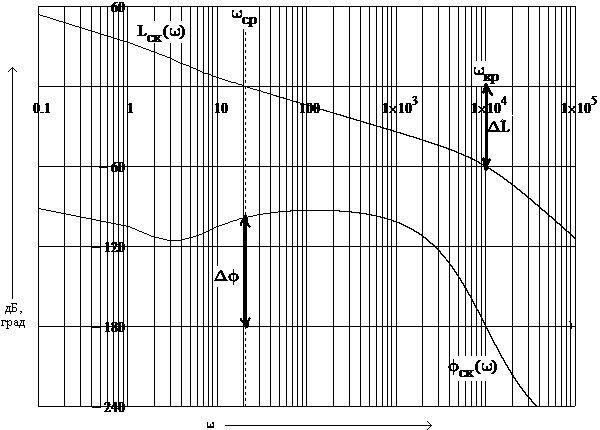
Рисунок 16 – ЛАХ и ФЧХ разомкнутой

системы последовательной коррекции

Вывод:

Оценки устойчивости замкнутой системы прямым методом и косвенным по критерию Найквиста показали, что система устойчивая. Выполнены коррекции звеньев для улучшения показателей качеств процесса регулирования замкнутой системы. В описании системы в пространстве различными способами, графики переходных процессов (рис. 13, рис 15) абсолютно одинаковые. Рассчитаны точность и критическое время запаздывания скорректированной системы.