3.4. Подчинённое регулирование координат в системе авк.

Замкнутые системы АВК реализуют не только с сумми-рующим усилителем, но и с подчинённым регулированием выпрямленного тока ротора асинхронного двигателя [9]. Cтруктурная схема такой системы приведена на рис. 3.6. Система регулирования двухконтурная с внутренним конту-ром выпрямленного тока ротора и внешним контуром скорос-ти.

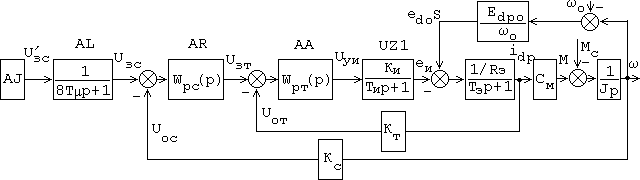
Рис. 3.6. Структурная схема системы АВК с подчинённым регулированием.

За малую некомпенсируемую постоянную времени Т принимается сумма малых постоянных времени: инвертора с системой импульсно-фазового управления и фильтра датчика тока. Как было показано выше Ти~(3...5)мс, величина постоянной времени фильта датчика тока зависит от аппа-ратной реализации датчика тока. Если датчик тока реали-зуют на базе шунта постоянного тока и УБСРовской ячейки датчика тока, то Тф.т.д ~(0,5...1,0)мс, если датчик тока реализуют на базе трансформаторов тока, включённых в фа-зы ротора с последующим выпрямлением сигнала, то Тф.т.д ~(1...3)мс. Большее значение посоянной времени фильтра обеспечит меньший уровень пульсаций в сигнале обратной связи по току.

Регуляторы тока АА и скорости АR обеспечивают ком-пенсацию больших постоянных времени в соответствующих контурах регулирования. Пренебрегая внутренней обатной связью по ЭДС ротора, оптимизацию контура тока можно осуществить по техническому оптимуму. Компенсации подле-ж-ит инерционность звена с передаточной функцией Wк(р)= =Ки/[Rэ(Тэр+1)]. Используя методику синтеза регуляторов, принятую для приводов постоянного тока [10], найдём пе-редаточную функцию регулятора тока:

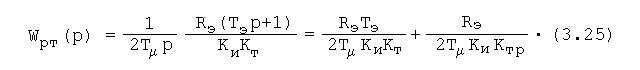
В нашем случае Т= Ти, так как цепь обратной связи по току изображена на рис. 3.6 безынерционной.

Регулятор тока получается пропорционально-интегаль-ным. Передаточная функция оптимизированного контура бу-дет иметь вид:

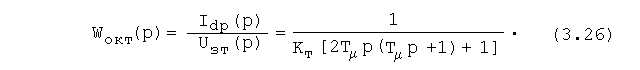
В связи с тем, что Rэ и Тэ в (3.25) зависят от ско-льжения, то для учёта этого следовало бы выполнить регу-лятор тока с переменными параметрами, зависимыми от S. Однако это сильно усложнит схему регулятора. Поэтому обычно регулятор тока выполняется с постоянными парамет-рами, но при этом контур тока будет оптимальным только при одном значении S, при котором выбрано Rэ. Настройка регулятора тока должна производиться при таких значениях Rэ и Тэ, чтобы при отклонении от оптимальной настройки запас устойчивости контура тока не снижался. Это обеспе-чивается при настройке регулятора при номинальном сколь-жении, когда Rэ = Rэmax, а Тэ = Тэmin. Тогда при регули-ровании скорости вниз от основной, скольжение будет воз-растать, и устойчивость контура тока будет повышаться. Примерный вид переходных процессов при разных значениях S показан на рис. 3.7,а.

В контуре скорости компенсаци подлежит действие звена с передаточной функцией Wкс(р) = См/(Jp).

Передаточная функция оптимизированного регулятора скорости будет иметь вид:

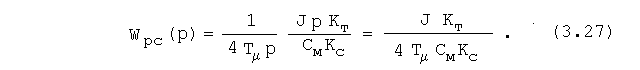
Регулятор скорости при настройке на технический оп-тимум получается пропорциональным. Передаточная функция оптимизированного контура скорости опишется выражением

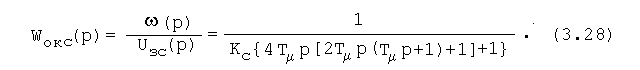
Полученные передаточные функции аналогичны соответ-ствующим передаточным функциям для двухконтурной систе-мы подчинённого регулирования электропривода постоянного тока [10].Для вышеописанной однократноинтегрирующей сис-темы АВК электромеханическая характеристика будет иметь подобный вид, как и для систем электропривода постоянно-го тока:

а) б)

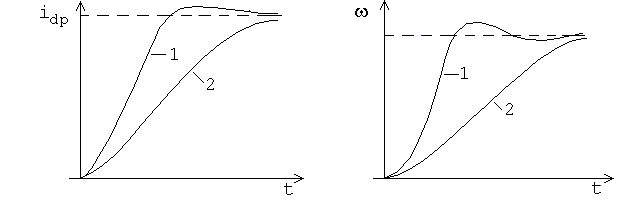
Рис. 3.7. Графики переходных процессов в АВК с подчинённым регулированием координат.

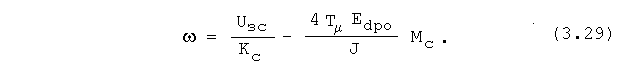
Если такой перепад скорости не удовлетворяет требо-ваниям производственного механизма, то оптимизацию кон-тура скорости как и в приводах постоянного тока прово-дят по симметричному оптимуму, в результате чего регуля-тор скорости получается пропорционально-интегральным с передаточной функцией:

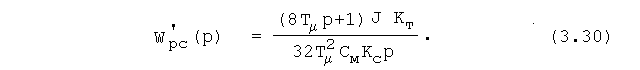
При этом система АВК становится двукратно-интегри-рующей, имеющей астатическую механическую характеристику со скоростью

 = Uзс/Кс. (3.31)

Для уменьшения величины перегулирования действие форсирующего звена в регуляторе скорости можно компен-сировать включением на вход системы апериодического зве-на с передаточной функцией Wф(р)= 1/(8Тp+1). В тех слу-чаях когда необходимо сформировать требуемый переходный процесс в системе, на вход включают задатчик интенсив-ности АJ (рис. 3.6).

Следует отметить, что коэффициент усиления регулятора скорости, равный в однократно-интегрирующей системе Крс= JКт/(4ТCмКс), а в двукратно-интегрирующей - Крс'= JКт/(32ТCмКс), зависит от коэффициента пропорци-ональности См между моментом и выпрямленным током рото-ра, который является переменным и зависит от изменения нагрузки. При настройке регулятора скорости, так же как и регулятора тока, значения параметров настройки прини-мают постоянными. Обычно регулятор скорости настраивает-ся при максимальном значении См = Edрo/о, при Idp = 0. Такая настройка регулятора скорости обеспечиет близкие к оптимальным переходные процессы при малых нагрузках (кривая 1 на рис. 3.7,б) и демпфирование скорости при больших нагрузках (кривая 2). Если такое снижение быст-родействия электропривода недопустимо, то следует прини-мать самонастраивающиеся регуляторы скорости и тока в зависимости от изменения нагрузки и скольжения.

При оптимизации системы АВК пренебрегают влиянием внутренней обратной связи по ЭДС ротора с целью упрощения оптимизации регулятора тока. Однако это прине-брежение правомерно только при больших значениях момен-та инерции электропривода. При малых значениях внутрен-няя обратная связь по ЭДС может оказывать значительное влияние на переходные процессы и снижать быстродействие системы. В этом случае следует принимать меры по компен-сации влияния внутренней обратной связи по ЭДС аналогич-но тому, как это делается в электроприводах постоянного тока.

При синтезе систем подчинённого регулирования АВК следует учитывать две особенности каскадов, заключающие-ся в отсутствии тормозных режимов и выбеге двигателя при Еи > ЕdpoS при изменении скольжения от нуля до единицы и меньшей возможности форсирования процессов, так как форсирующее действие системы связано с уменьшением выхо-дного сигнала ЭДС инвертора, предел регулирования кото-рого равен нулю.

Пример. С помощью моделирующей программы SMOD [14] расчитать и построить динамические характеристики систе-мы, приведённой на рис.3.6.

В качестве исполнительного двигателя в системе ис-пользован двигатель с фазным ротором типа 4АНК355S6У3 со следующими характеристиками: Рн=200 кВт; н= 101,5 1/c; I2= 411 А; Е2н= 304 В; о=104,7 1/c; R1=0,025 Ом; х1=0,13 Ом; R2=0,27 Ом; х2=0,16 Ом; J=7,8 кГ м2. В качес-тве инвертора использован инвертор типа АТ 800/460-2 с техническими характеристиками: Udн=460 В; Idн=800 A; Хтр=0,016 Ом; Rтр=0,06 Ом. В цепь выпрямленного тока включён сглаживающий дроссель типа ФРОС с Lдр=2,3 10-3 Гн; Rдр=4,7 10-3 Ом.

Произведём расчёт параметров звеньев структурной схе-мы, приведённой на рис.3.6.

Еdpo= 1,35 Е2н = 1,35 304= 410 В.

Коэффициент пропорциональности между моментом и то-ком двигателя определим по выражению (3.20,а):

См=[Еdpo - mвХдIdср/(2)]/о =

= [410-6 0,24 504/6,28]/104,7 = 2,81 В с,

где Хд = Х2 + Х1/Ке2 = 0,16 + 0,13/1,56 = 0,24 Ом;

Idср = Idн = I2н/0,815 = 504 A.

Эквивалентное сопротивление цепи выпрямленного тока ротора Rэ определяется как

Rэ = 2R1' S + 2R2 + mвХдS/(2) + Rдр + 2Rтр + mиХт/(2)=

= 2 0,016 0,03 + 2 0,027 + 6 0,24 0,03/6,28 + 4,7 10-3

+ 2 0,06 + 6 0,016/6,28 = 0,2 Ом,

где R1' = R1/Ке2= 0,025/1,56 = 0,016 Ом;

S = Sн = (о-н)/о = (104,7-101,5)/104,7 = 0,03.

Эквивалентную постоянную времени Тэ цепи выпрямле-н-ного тока ротора найдём как:

Тэ = Lэ/Rэ = 0,004/0,2 = 0,02 c,

где Lэ = 2Lд + Lдр + 2Lтр= (2 0,24)/314 + 2,3 10-3+

+ (2 0,016)/314 = 0,004 Гн.

Коэффициент передачи инвертора определим по регули-ровочной характеристике преобразователя в районе рабочей точки Ки=Еdи/Uуи= 47. Постоянную времени инвертора Tи принимаем равной 4 10-3 с.

Значения коэффициентов обратных связей по току и скорости расчитаем по выражениям

Кт=Uзт max/Idp max= 10/2 Idpн= 10/(2 504) = 0,01 Ом;

Кс=Uзс max/о = 10/104,7 = 0,096 В с.

Передаточная функция регулятора тока, согласно (3.25), будет иметь вид:

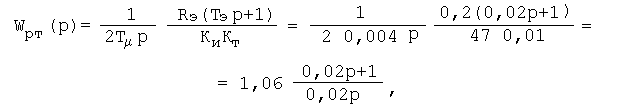а передаточная функция регулятора скорости в соот-ветствии с выражением (3.30) примет вид:

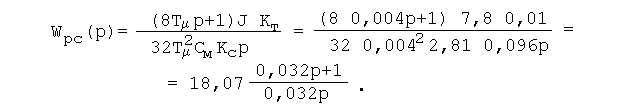Таким образом, схема, подвергаемая исследованию в качестве модели, примет вид, показанный на рис.3.8.

В качестве примера на рис.3.9 приведены кривые ре-ации системы на скачок входного воздействия при отсутст-

Рис.3.9. Динамические характеристики системы.]

вии нагрузки на валу двигателя и при наличии ограничения выходного напряжения регулятора скорости.