5. Асинхронный электропривод с частотным

УПРАВЛЕНИЕМ

5.1. Определение способа частотного управления ско-ростью асинхронного двигателя.

Из теории электропривода, известно, что синхронная скорость ротора АД

где рп - число пар полюсов машины; f1 - частота напря-жения статора.

Это даёт возможность регулировать скорость АД изме-нением частоты f1 напряжения, питающего статор.

При частотном регулировании возможна работа АД в широком диапазоне скоростей с малым скольжением, что снижает потери электроэнергии в машине и обеспечивает высокий КПД АД. Коэффициент мощности АД с уменьшением скольжения и частоты f1 растёт в следствии снижения па-дений напряжения на индуктивных элементах машины. Часто-тное регулирование является едиственно возможным спосо-бом получения очень высоких скоростей вращения (до 300000 об/мин). Применение соответствующих замкнутых систем автоматического управления позволяет строить час-тотно-регулируемые электроприводы с достаточно большим диа-пазоном регулирования скорости D=1:(20...30) и хоро-шим быстродействием.

Для обеспечения постоянной перегрузочной способнос-ти двигателя, хорошей линейности его механических харак-теристик и ненасыщения его магнитной системы необходимо с изменеием частоты напряжения статора изменять и амплитуду этого напряжения.При всех практически приемли-мых способах частотного регулирования уменьшение частоты напряжения статора должно сопровождаться уменьшением его амплитуды, и наоборот: увеличение частоты сопровождается увеличением амплитуды. Поэтому в качестве источников пи-тания таких электроприводов используют источники пере-менного напряжения, желательно синусоидального, с регу-лируемой частотой и амплитудой. Несинусоидальность на-пряжения источника питания обуславливает дополнительные потери в цепях двигателя от высших гармонических тока.

Основной недостаток частотно-регулируемых электро-приводов - сложность технической реализации силовых ис-точников питания с раздельными каналами регулирования частоты и амплитуды напряжения, имеющих хорошее быстродействие и форму напряжения, близкую к синусоида-льной.

Однозначность в управлении скоростью и моментом АД возможна лишь при формировании в виде независимых коор-динат потока двигателя или тока статора. При рассмат-риваемом здесь способе частотного управления в качестве управляющих воздействий используются частота и напряже-ние статора. Данный способ частотного управления следует отличать от способа частотно-токового управления, при котором в качестве управляющих воздействий принимаются частота и ток статора.

5.2. Статические режимы АД при частотном управлении

Схема замещения одной фазы АД при частотном регули-ровании приведена на рис. 5.1., где U1н - действующее номинальное напряжение фазы статора; = U1/U1н - относи-тельное напряжение фазы статора (U1 - произвольное дей-ствующее значение напряжение фазы статора); Е1 - ЭДС фазы статора; Е2 - приведённая к статору ЭДС фазы рото-ра; R1 - активное сопротивление фазы статора; I1 - ток фазы статора;  = 1/1н - относительная частота напря-жения статора (1 - угловая частота напряжения ста-тора; 1н - номинальное значение угловой частоты напря-жения статора); х1 - индуктивное сопротивление фазы ста-тора на частоте 1н; х'2 - приведённое к статору индук-тивное сопротивление фазы ротора на частоте 1н; хm- ин-дуктивное сопротивление намагничивающей цепи машины при частоте 1н; R'2 - приведённое к статору активное сопро-тивление фазы ротора; I'2 - приведённый к статору ток фазы ротора; S2 - параметр абсолютного скольжения.

Рис. 5.1. Схема замещения фазы АД.

Параметр абсолютного скольжения - это отношение уг-ловой частоты ЭДС ротора 2 (приведённой к двухполюсному двигателю) к 1н:

где  - угловая скорость ротора; о - синхронная угловая скорость ротора при произвольной частоте напря-жения статора 1; он - синхронная номинальная cкорость ротора (при частоте 1н); S=(1-pп)/1 - скольжение двигателя (при произвольной частоте напряжения статора 1).

Как показано в [11] из расчёта схемы замещения в установившемся режиме имеем приведённые в табл.5.1 соот-ношения регулируемых координат и параметров короткозам-кнутого АД при частотном управлении. В данной таблице, кроме упомянутых выше, приняты следующие обозначения: М - электромагнитный момент двигателя; - поток двигате-ля;

А(,S2)=(b2+с22)S22 + 2R1R2'S2 + (d2+е22)R2'2;

В(S2)=R2'2+ х2'2S2;

D(S2) = R2'2/хm2 + K2S22;

С(S2) = R2'2/хm2 + (1+K2)2S22;

b = R1(1+K2); с = хmK; d = R1/xm; e = 1+K1;

где С1 - конструктивная постоянная двигателя; m1 - число фаз статора; /н - относительный поток двига-теля (н - номинальное значение потока); K1, K2, K -

Таблица 5.1.

коэффициенты рассеяния, соответственно, для статора (K1= х1/xm), ротора (K2= х2'/xm) и общий (K = =K1+K2+K1K2).

При обеспечении стабилизации  или I1 и фикси-рованном значении все остальные параметры двигателя однозначно зависят от S2.

Когда регулирование производится при напряжении, не засящем от нагрузки двигателя, то абсолютное критическое скольжение

а максимальный момент

В последних формулах знак "+" соответствует двига-тельному режиму АД, а знак "-" - режиму генераторного торможения.

При анализе статических характеристик АД использо-валась Т-образная схема замещения. В справочной литера-туре обычно приводятся параметры для Г-образной схемы замещения. Для АД нормального исполнения мощностью выше нескольких киловатт значения параметров Г-образной схемы практически не отличаются от соответствующих им значений параметров Т-образной схемы и могут быть использованы при расчётах статических характеристик АД по приведённой выше методике.

Рассмотрим некоторые используемые на практике спо-собы частотного управления АД в статике и соответ-ствующие им механические характеристики.

Способ . Он легко реализуется в разомкнутых системах электропривода, имеющих приведённую на рис.5.2. функциональную схему, на которой приняты следующие обоз-начения: Uзс - сигнал задания скорости АД; ПЧ - преоб-разователь частоты; ФП - функциональный преобразователь (в данном случае пропорциональное звено), обеспечивающий при изменении Uзс выполнение в статике соотношения ; РЧ - канал регулирования частоты с коэффициентом Кр; РН - канал регули-рования напряжения c коэффициентом Кр; ПЧ - преобразователь частоты; Uусиг-нал управления часто-той ПЧ; Uу - сигнал управления ЭДС ПЧ; Uс - напряжение питающей сети.

Для компенсации влияния внутреннего сопротивления ПЧ на его выходное напряжение, то есть обеспечения жёст-кой внешней характеристики ПЧ, может использоваться показанный на рис.5.2. пунктиром канал отрицательной обратной связи ОСН по выходному напряжению ПЧ, где Uз - сиг-нал задания напряжения; Uос - сигнал обратной связи по напряжению.

Рис. 5.2. Функциональная схема системы.

Пример 1. Построить статистические характеристики АД типа 4А160S4У3, работающего в системе, функциональная схема которой приведена на рис. 5.2.

Параметры АД: синхронная угловая скорость вращения ротора он = 157 с-1; номинальная мощность на валу Р2н= 15 кВт; кпд при номинальной нагрузке на валу 0,885; но--ми-нальная скорость н = 153,4 с-1; номинальный вращаю-щий момент Mн = 97,8 Н.м; критический момент Mк= 224,9 Н.м; номинальное фазное напряжение статора U1н= 220 В; но-минальный ток фазы I1н= 29,2 А; момент инерции рото-ра Jр = 0,1 кг.м2; пусковой ток фазы Iп= 180 А; индуктивное со-противление цепей намагничивания хm= 30,14 Ом; активное сопротивление фазы статора r1= 0,35 Ом; индук-тивное сопротивление фазы статора х1= 0,65 Ом; приве-дённое к статору активное сопротивление фазы ротора R2'= =0,19 Ом; приведённое к статору индуктивное сопротивле-ние фазы ротора х2'= 0,98 Ом; номинальная частота напря-же-ния статора f1н= 50 Гц; конструктивный коэффициент дви-гателя С1= 455.

Диапазон регулирования частоты напряжения статора 10...60 Гц. Способ частотного регулирования в статике . Максимально допустимое напряжение Uзс не более 10 В. Возможные отклонения напряжения сети, питающей ПЧ, от номинального значения +10 ; эквивалентное активное сопротивление фазы ПЧ Rпч= 0,2 Ом. В электроприводе воз-можны кратковременные перегрузки двигателя до значений статического момента, равных 1,76 Мн. Статическая ошибка регулирования напряжения на статоре при номинальном напряжении и максимальном токе статора на нижней границе диа-пазона регулирования скорости U1 = 2 от U1.

Требует-ся также определить коэффициенты передачи всех элементов функциональной схемы электропривода.

В качестве ПЧ используется автономный инвертор на-пряжения с управляемым выпрямителем на входе.

Все дейст-вующие в системе информационные сигналы име-ют размерность напряжений. Коэффициент усиления ПЧ по входу регулирования его ЭДС Кпч=30. Коэффициент переда-чи ПЧ по входу регулирования частоты Кпч = 8 Гц/В.

Определить необходимое значение максимальной ЭДС ПЧ.

Структурная схема контура регулирования напряжения ПЧ приведена на рис.5.3, где кроме вышеупомянутых приняты следующие обозначения: Eпч - фазная ЭДС ПЧ; Uпч - падение напряжения на внутреннем сопротивлении фазы ПЧ; Крн - коэффициент усиления корректирующего звена в канале регулирования напряжения; Косн - общий коэф-фициент усиления канала обратной связи по напряжению.

Рис.5.3. Структурная схема контура регулирования

напряжения ПЧ.

Полагаем, что до значения момента на валу двигате-ля, равного Mк, ток статора двигателя примерно пропорци-онален его моменту. Для рассматриваемого АД Mк= 2,3Mн и ток статора при максимальном моменте на валу, равном 1,76 Mн, будет соответственно равен I1max= 1,76 I1н= 51,36 А. При этом максимальное падение напряжения в ста-тике на внутреннем сопротивлении ПЧ будет Uпч max= I1max .Rпч= 51,36 . 0,2= 10,2 В. При рассматриваемом способе ре-гу-лирования max= max= 60 Гц/50 Гц = 1,2, а min= min= = 10 Гц/50 Гц = 0,2. Требуемое действующее значение мак-симальной фазной ЭДС ПЧ (с учётом 10 / колебаний напря-жения сети и падения напряжения на Rпч).

Eпч max'= max. U1н.(1+(10 / /100 / ))+ Uпч max=

= 1,2 . 220 (1 + 0,1) + 10,2 = 300,6 В.

Минимальное значение напряжения статора на нижней границе диапазона регулирования скорости U1 min= U1н . min= 200 . 0,2 = 44 В, а максимальное на верхней границе U1 max=U1н . max = 220 . 1,2 = 264 В. Ошибка регулирова-ния напряжения на нижней границе диапазона U1=(U1 / /100 / ).U1min= (2/100).44 = 0,88 В. Эдс ПЧ на нижней границе диапазона регулирования Епч min= U1 min+ U1= 44+ 0,88 = 44,88 В.

Статика схемы на рис. 5.3 описывается системой уравнений:

(Uз - Uос) Кр . Кпч = Епч;

Епч - I1Rпч = U1;

U1 . Кос = Uос,

из которой имеем уравнение внешней характеристики ПЧ с обратной связью по напряжению:

Напряжение задания на нижней границе диапазона ре-гулирования

Uз min = Uз max . max/min = 10 . 0,2/1,2 = 1,67 В.

На нижней границе диапазона регулирования при мак-симальном токе статора должно выполняться условие:

На основании данного условия и после подстановки в него известных численных значений коэффициентов и пара-метров может быть составлена система уравнений:

из которой определяется коэффициенты Кр = 10,91 и Кос = =0,0341.

В дальнейшем решении контур регулирования напряже-ния с достатояной точностью может быть представлен одним звеном с коэффициентом

а влияние внутреннего сопротивления ПЧ может учтено внесением в фазу АД дополнительного активного сопротив-ления

В связи с тем, что внешняя характеристика ПЧ не об-ладает бесконечно большой жёсткостью, необходимо уточ-нить максимальное значение напряжения Uз , при котором в системе при I1 = I1max устанавливается значение напря-жения U1 = U1max .

Так как внешние характеристики в рассматриваемой системе при изменении Uз располагаются параллельно друг другу, значение ЭДС ПЧ при U1 = U1max = 264 В и номиналь-ном напряжении сети равно

Епч max = U1max + U1= 264 + 0,88 = 264,88 В.

или К Uзн max = 264,88.

Из последнего выражения следует, что уточненное зна-чение

Uз max = 264,88/26,84 = 9,87 В.

Нетрудно видеть, что из-за неидеальности использо-ванного в системе источника напряжения (Rпч  0),

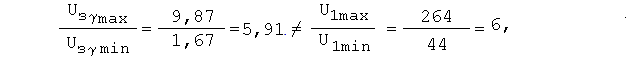то есть в такой системе невозможно добиться строгого вы--полнения закона регулирования в структуре (см. рис. 5.3) с использованием простого линейного ФП. Однако вследствии малого различия между правой и левой частью данного неравенства вышесказанным при практических расчётах можно пренебречь.

При использовании контура регулирования напряжения ПЧ с интегральной составляющей R1доп = 0 внешняя харак-теристика ПЧ имеет бесконечно большую жёсткость, и, соответственно, применение линейного ФП обеспечит точное выполнение рассматриваемого закона регулирования при любых токах статора.

Определяем коэффициент ФП:

Кфп = Uз max/Uзc max = 9,87/10 = 0,987

и коэффициент корректирующего звена в канале регулиро-вания частоты

Кр = f1 max/(Кпч . Uзс max) = 60/(8 . 10) = 0,75.

В соответствии со структурой схемы и выражением (5.1) при максимальном I1 имеем для ряда значений Uзс следующие значения и:

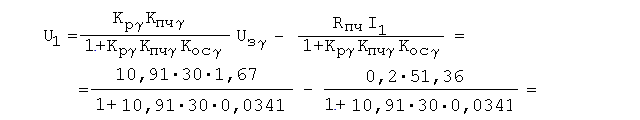
Uу = Uзс.Кp = 1,69 . 0,75 = 1,267 В;

f1 = Uу.Кпч = 1,267 . 8 = 10,1 Гц;

= f1/f1н = 10,1/50 = 0,2.

Аналогично имеем для

Uзс = 6 В; = 0,72; = 0,72;

Uзс = 10 В; = 1,2; = 1,2.

Далее для каждого из значений Uзс и соответствую-щих ему значений  и рассчитывают в функции скольжения S2 величины M, , I1, E1. При расчётах используются формулы из таблицы 5.1 (из столбца "Значение величины в общем виде"). Скорость ротора определяется по формуле:

 = (1 - S2.1н)/pп,

где 1н = 2f1н = 2 . 3,14 . 50 = 314 с-1; pп = 2;

1 = 2f1н . 314 . с-1.

Сопротивление цепи статора R1 в расчётах взято рав-ным r1 + R1доп = 0,35 + 0,016 = 0,366 Ом.

Результаты расчёта приведены в табл.5.2.

Таблица 5.2

S2 (с-1) M(Н.м) I1(А) (Вб) Е1(В)

1 2 3 4 5 6

Uзс = 1,69 В; = 0,2;  = 0,2

-0.2 62.83 -233.26 117.12 0.0068 30.95

-0.15 54.98 -350.48 124.38 0.0085 38.55

-0.1 47.12 -562.34 128.77 0.0117 53.23

-0.0775 43.59 -626.34 119.78 0.0134 61.07

-0.05 39.27 -467.64 83.50 0.0138 63.00

0.0 31.41 0.0 7.13 0.0094 42.99

Продолжение таблицы 5.2.

1 2 3 4 5 6

0.05 23.56 99.43 38.50 0.0064 29.05

0.0775 19.24 105.09 49.06 0.0055 25.02

0.1 15.70 103.12 55.14 0.0050 22.79

0.15 7.87 92.83 64.01 0.0044 19.84

0.2 0.0 81.93 69.41 0.0040 18.34

0.25 -7.85 72.55 73.02 0.0038 17.53

0.3 -15.70 64.80 75.59 0.0037 17.08

0.35 -20.35 58.40 77.50 0.0037 16.82

0.4 -31.41 53.08 79.00 0.0037 16.66

0.45 -39.27 48.61 80.17 0.0036 16.57

0.5 -47.12 44.81 81.14 0.0036 16.51

0.55 -54.98 41.55 81.94 0.0036 16.49

0.6 -62.83 38.72 82.62 0.0036 16.48

0.65 -70.63 36.24 83.19 0.0036 16.48

0.7 -78.54 34.06 83.62 0.0036 16.48

0.75 -86.39 32.12 84.13 0.0036 16.49

0.8 -94.25 30.39 84.51 0.0036 16.50

0.85 -102.10 28.83 84.85 0.0036 16.52

0.9 -109.95 27.42 85.16 0.0036 16.53

0.95 -117.81 26.15 85.43 0.0036 16.55

1.0 -125.66 24.98 85.68 0.0036 16.57

1.05 -133.51 23.92 85.90 0.0036 16.58

Uзс = 6 В; = 0,72;  = 0,72

-0.2 144.51 -294.88 131.69 0.0076 125.28

-0.15 136.66 -345.51 123.50 0.0084 137.80

-0.112 130.70 -366.28 109.97 0.0091 149.97

-0.1 128.80 -362.99 103.46 0.0094 153.95

-0.05 120.95 -247.15 70.70 0.0100 164.89

0.0 113.09 0.0 7.14 0.0095 155.03

0.05 105.24 160.11 48.86 0.0081 132.71

0.1 97.39 201.83 77.14 0.0070 114.80

0.112 95.50 202.85 81.84 0.0068 111.60

0.15 89.53 196.31 93.09 0.0063 103.87

0.2 81.68 178.86 102.56 0.0059 97.57

0.25 73.83  160.49 108.60 0.0057 93.89

0.3 65.97 114.04 112.70 0.0056 91.68

0.35 58.12 129.96 115.62 0.0055 90.31

0.4 50.26 118.02 117.78 0.0055 89.44

0.45 42.41 107.90 119.45 0.0054 88.87

0.5 34.56 99.26 102.76 0.0054 88.50

0.55 26.70 91.83 121.82 0.0054 88.26

0.6 18.85 85.38 122.69 0.0054 88.10

0.65 10.10 79.75 123.41 0.0054 88.00

0.7 3.14 74.79 124.03 0.0054 87.94

Продолжение таблицы 5.2.

1 2 3 4 5 6

0.75 -4.71 70.40 124.55 0.0054 87.91

0.8 -12.57 66.48 125.00 0.0054 87.90

0.85 -20.42 62.97 125.40 0.0054 87.90

0.9 -28.27 59.81 125.75 0.0054 87.91

0.95 -36.13 56.94 126.07 0.0054 87.92

1.0 -43.98 54.33 126.34 0.0054 87.95

1.05 -51.84 52.95 126.59 0.0054 87.97

Uзс = 10 В; = 1,2;  = 1,2

-0.2 219.91 -275.47 127.28 0.0074 201.81

-0.15 212.05 -314.13 117.75 0.0080 219.00

-0.1154 206.63 -327.27 105.52 0.0086 234.53

-0.1 204.20 -323.20 97.62 0.0089 242.11

-0.05 196.35 -225.48 57.98 0.0096 262.45

0.0 138.49 0.0 7.14 0.0095 258.41

0.05 180.64 173.77 50.90 0.0084 230.43

0.1 172.79 226.56 31.74 0.0074 202.71

0.1154 170.36 228.55 88.18 0.0072 195.95

0.15 164.93 222.06 99.00 0.0067 184.13

0.2 157.08 202.02 109.00 0.0063 172.83

0.25 149.22 180.51 115.18 0.0061 165.96

0.3 141.37 161.26 119.24 0.0059 161.67

0.35 133.52 144.85 122.06 0.0058 158.91

0.4 125.66 131.04 124.11 0.0057 157.07

0.45 117.81 119.39 125.65 0.0057 155.81

0.5 109.95 109.50 126.83 0.0057 154.92

0.55 102.10 101.03 127.78 0.0056 154.30

0.6 94.25 93.72 128.54 0.0056 153.84

0.65 86.39 87.36 129.16 0.0056 153.52

0.7 78.54 81.78 129.69 0.0056 153.27

0.75 70.68 78.85 130.14 0.0056 153.09

0.8 62.83 72.47 130.52 0.0056 152.95

0.85 54.98 68.66 130.85 0.0056 152.85

0.9 47.12 65.03 131.13 0.0056 152.78

0.95 39.27 61.85 131.39 0.0056 152.73

1.0 31.41 58.96 131.61 0.0056 152.69

1.05 23.56 56.32 131.81 0.0056 152.66

На рис.5.4 приведены механические характеристики, построенные по результатам расчёта. Как следует из рису-нка, максимальный момент в двигательном режиме с умень-шением частоты и напряжения статора уменьшается. Это

связано с уменьшением потока двигателя при критических значениях S2.

По данной методике могут быть расcчитаны параметры двигателя в номинальном режиме, то есть при = 1, S2= =Sн = 0,0229:

н = 153,482 с-1; Mн = 95 Н.м; Iн = 26,15 А;

н = 0,0090 Вб; Е1н = 204,48 В,

которые лишь незначительно отличаются от снятых экспери-ментально каталожных данных двигателя.

Способ регулирования U1н = .U1н + R1I1, или = UR1, где UR1 = R1I1/U1н - относительное падение напряжения на активном сопротивлении цепи тока фазы статора.

Для реализации этого способа регулирования в сис-тему электропривода должна быть введена положительная об-ратная связь по току статора, как показано на фун-кциональной схеме (рис.5.2) штрих-пунктирной линией, где UосI - напряжение положительной обратной связи по току.

Если коэффициент передачи датчика тока ДТ будет ра-вен R1, то для полной компенсации падения напряжения на сопротивлении цепи статора R1 необходимо иметь коэффици-ент усиления в канале обратной связи по току

КIR = Кдт Ккз = R1 Ккз = 1/К,

где Ккз- коэффициент усиления корректирующего звена. В рассматриваемом примере: КIR = 1/26,84 = 0,0372; Ккз= =0,0372/0,366 = 0,102.

В такой системе статические характеристики могут быть с достаточной точностью рассчитаны также по фор-мулам табл.5.1, полагая, что в этих формулах сопротив-ление R1 = 0. Результаты расчёта статистических харак-теристик рассматриваемой выше системы для данного случая приведены в табл.5.3 для двух значений напряжения за-дания скорости в функции скольжения S2.

Механические характеристики, построенные по данным табл.5.3, приведены на рис.5.4 штриховой линией.

Таблица 5.3

S2 (с-1) M(Н.м) I1(А) (Вб) Е1(В)

1 2 3 4 5 6

Uзс = 6 В;  = 0,72

-0.2 144.51 -239.40 118.66 0.0069 112.88

-0.15 136.66 -226.07 108.37 0.0074 120.93

-0.1175 131.56 -274.01 97.41 0.0078 128.22

-0.1 128.80 -270.47 89.31 0.0081 132.89

-0.05 120.95 -197.38 34.25 0.0090 147.35

0.0 113.10 0.0 7.14 0.0095 155.06

0.05 105.24 197.38 54.25 0.0090 147.35

0.1 97.39 270.47 89.31 0.0081 132.89

0.1175 94.63 274.01 97.41 0.0078 128.22

0.15 89.53 266.07 108.37 0.0074 120.93

0.2 81.68 239.40 118.66 0.0069 112.83

0.25 73.83 211.03 124.53 0.0066 107.66

0.3 65.97 186.16 128.12 0.0064 104.22

0.35 58.12 165.40 130.43 0.0062 101.88

0.4 50.26 148.25 132.00 0.0061 100.24

0.45 42.41 134.01 133.12 0.0060 92.04

0.5 34.56 122.09 133.93 0.0060 98.16

0.55 26.70 112.01 134.54 0.0060 97.48

0.6 18.85 103.40 135.01 0.0060 96.96

0.65 10.99 95.97 135.38 0.0059 96.54

0.7 3.14 89.51 135.68 0.0059 96.20

0.75 -4.71 83.84 135.92 0.0059 95.94

0.8 -12.57 78.82 136.11 0.0058 95.71

0.85 -20.42 74.37 136.28 0.0058 95.52

0.9 -28.27 70.38 136.41 0.0058 95.36

0.95 -36.13 66.79 136.53 0.0058 95.22

1.0 -43.98 63.54 136.63 0.0058 95.11

1.05 -51.84 60.59 136.72 0.0058 95.01

Uзс = 1,69 В;  = 0,2

-0.2 62.83 -239.40 118.66 0.0069 31.36

-0.15 54.98 -266.07 108.37 0.0074 33.59

-0.1175 49.88 -274.01 97.41 0.0078 35.62

-0.1 47.12 -270.47 89.31 0.0081 36.91

-0.05 39.27 -197.38 54.25 0.0090 40.93

0.0 31.41 0.0 7.41 0.0095 43.07

0.05 23.56 197.38 54.25 0.0090 40.93

0.1 15.71 270.47 89.31 0.0081 36.91

0.1175 12.95 274.01 97.41 0.0078 35.62

Продолжение таблицы 5.3.

1 2 3 4 5 6

0.15 7.85 266.07 108.37 0.0074 33.59

0.2 0.0 239.40 118.66 0.0067 31.36

0.25 -7.85 211.03 124.53 0.0066 29.91

0.3 -15.71 186.16 128.12 0.0064 28.95

0.35 -23.56 165.40 130.43 0.0062 28.30

0.4 -31.41 148.25 132.00 0.0061 27.84

0.45 -39.27 134.01 133.12 0.0060 27.51

0.5 -47.12 134.01 133.93 0.0060 27.27

0.55 -54.98 112.01 134.54 0.0060 27.08

0.6 -62.83 103.40 135.01 0.0060 26.93

0.65 -70.68 95.97 135.38 0.0059 26.82

0.7 -78.54 89.51 135.68 0.0059 27.72

0.75 -86.39 83.84 135.92 0.0058 26.65

0.8 -94.25 78.82 136.12 0.0058 26.58

0.85 -102.10 74.37 136.28 0.0058 26.53

0.9 -109.95 70.38 136.42 0.0058 26.49

0.95 -117.81 66.79 136.53 0.0058 26.45

1.0 -125.66 63.54 136.63 0.0058 26.42

1.05 -133.52 60.59 136.72 0.0058 26.39

При рассматриваемом способе частотного регулирова-ния обеспечивается постоянная перегрузочная способность двигателя и увеличивается жёсткость механических харак-теристик.

Используется также способ регулирования при посто-янном потоке двигателя .

Из таблицы 5.1. следует, что

Е1= Е1н E1н (/н);

 = (н/E1н)(Е1/).

Поэтому, если в процессе регулирования скорости под-держивать постоянным отношение ЭДС двигателя Е1 к час-тоте статора , будет сохраняться постоянство потока двигателя , а значит будет обеспечиваться хорошая ли-нейность механических характеристик и постоянная пере-грузочная способность двигателя.

При таком регулировании расчёт механических харак-теристик производится по формуле (см. табл. 5.1)

из столбца, соответствующего независимому ма-гнитному потоку .

Для реализации такого способа управления в системе регулирования электроприводом должен быть контур стаби-лизации ЭДС двигателя Е1. Причём задание на частоту  и ЭДС двигателя Е1 должно изменяться одинаково.

Функциональная схема такого электропривода приведе-на на рис.5.2. В электроприводе, как указано на схеме в скобках, используется датчик ЭДС ДЭ. Сигнал обратной свя-зи по ЭДС UосЕ со знаком "-" заводится на вход сумма-тора. На другой вход сумматора подаётся сигнал задания ЭДС двигателя UзЕ. Указанная пунктиром обратная связь по напряжению ПЧ(см. рис. 5.2) может быть исключена.

Пример 2. Для двух произвольных значений напряжения задания скорости Uзс построить статические характеристи-ки АД типа 4А160S4У3, управляемого при постоянном =н. Функциональная схема электропривода приведена на рис. 5.2. В схеме должна быть оставлена только одна обратная связь по ЭДС, показанная штрих-пунктирной линией. Пас-портные параметры двигателя приведены в рассмотренном выше примере 1. Диапазон измерения частоты напряжения ста-тора от 10 до 60 Гц. Максимально допустимое напряже-ние Uзс не более 10 В.

В контуре регулирования ЭДС двигателя присутствует интегральная составляющая. Коэффициент усиления датчика ЭДС КДЭ=30.

Коэффициент передачи ПЧ по входу регулирования час-тоты КПЧ = 8 Гц/В.

Значения номинальной ЭДС двигателя и его номиналь-ного потока определены в решении примера 1 и равны Е1н= =204,48 В, =0,0090 Вб.

Требуется также определить необходимые в статике значения коэффициентов структурной схемы системы элек-тро-привода.

Полагая, что Uзсmax=Кp КПЧ = f1max, имеем

Кp = f1max/(Uзсmax КПЧ)= 60/(10 8)=0,75.

При номинальной частоте f1 = f1н = 50 Гц напряжение задания скорости будет равно

Uзсн = Uзсmax (f1н/f1max)= 10 (50/60) = 8,33 B.

Полагая, что при наличии интегральной составляющей в контуре регулирования ЭДС, статическая ошибка регу-лирования ЭДС равна нулю, а значение UзЕ в номинальном режиме равно UзЕн=8,33 В, имеем для номинального режима:

UзЕн - UосЕн = 0; UзЕн - КДЭ Ккз Е1н = 0,

из чего следует, что статический коэффициент корре-кти-рующего звена

Ккз = UзЕн/(КДЭ Е1н) = 8,33/(30 204,48)= 0,00136.

Cтатический коэффициент усиления функционального преобразователя находится как

Кфп= UзЕн/Uзсн = 8,33/8,33 = 1.

Значения Uзс связаны с относительной частотой ста-тора соотношением Uзс = Uзсн .

Результаты расчёта статических характеристик для двух значений напряжения Uзс приведены в таблице 5.4. Графики расчитанных характеристик приведены на рис. 5.4 штрих-пунктирной линией.

Таблица 5.4.

S2 (с-1) M(Н.м) I1(А)

1 2 3 4

Uзс = 8 В;  = 0,2; Е1= 196,3 В

-0.2 182.21 -407.23 154.76

-0.15 174.36 -394.40 131.94

-0.1 166.50 -332.00 98.94

-0.05 158.65 -197.04 54.20

0.0 150.80 0.0 6.78

0.05 142.94 197.04 54.20

0.1 135.09 332.00 98.94

0.15 127.23 394.40 131.94

0.2 119.38 407.23 154.76

0.25 111.53 394.60 170.29

0.3 103.67 371.46 180.98

0.35 95.82 345.39 188.48

0.4 87.96 319.82 193.89

0.45 80.11 296.10 197.87

0.5 72.26 274.66 200.88

0.55 64.40 255.49 203.19

0.6 56.55 238.41 205.01

0.65 48.69 223.19 206.46

0.7 40.84 209.61 207.63

0.75 32.99 197.45 208.59

0.8 25.13 186.52 209.38

0.85 17.28 176.67 210.05

0.9 9.42 167.75 210.61

0.95 1.57 159.65 211.09

1.0 -6.28 152.26 211.50

1.05 -14.18 145.50 211.86

Uзс = 4 В;  = 0,48; Е1= 98,15 В

-0.2 106.81 -407.23 154.76

-0.15 98.96 -394.40 131.94

-0.1 91.11 -332.00 98.94

-0.05 83.25 -197.04 54.20

0.0 75.40 0.0 6.78

0.05 67.54 197.04 54.20

0.1 59.69 332.00 98.94

0.15 51.89 394.40 131.94

0.2 43.98 407.23 154.76

0.25 36.13 394.60 170.29

0.3 28.27 371.46 180.98

Продолжение таблицы 5.4.

1 2 3 4

0.35 20.42 345.39 188.48

0.4 12.57 319.82 193.89

0.45 4.71 296.10 197.87

0.5 -3.14 274.66 200.88

0.55 -10.99 255.49 203.19

0.6 -18.85 238.41 205.01

0.65 -26.70 223.19 206.46

0.7 -34.58 209.61 207.63

0.75 -42.41 197.45 208.59

0.8 -50.26 186.52 209.38

0.85 -58.12 176.67 210.05

0.9 -65.97 167.75 210.61

0.95 -73.83 159.65 211.09

1.0 -81.68 152.26 211.50

1.05 -89.53 145.50 211.86