4.6.2. Механические характеристики электропривода с астатической сар скорости

Соотношения между входными и выходными переменными в установившихся режимах можно получить из операторных уравнений реакций двукратной САР путем подстановки р = 0:

;

.

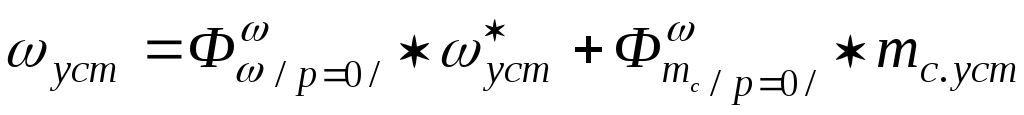С учетом полученных выше выражений передаточных функций двукратной САР (4.33) – (4.36) в результате получаем:

.

Таким образом, электропривод с двукратной САР скорости действительно обладает абсолютно жесткой статической механической характеристикой, т.е. в установившемся режиме скорость двигателя зависит только от задания и не зависит от нагрузки.

В установившихся режимах момент двигателя зависит только от нагрузки и не зависит от задания, что полностью соответствует уравнению движения электропривода.

Графики механических характеристик электропривода с одно- и двукратной САР скорости изображены на рис. 4.26.

Рис. 4.26. Статические механические характеристики электропривода

с различными системами регулирования скорости:

—— Двукратной САР; - - - Однократной САР

Главным достоинством двукратных САР является лучшая стабилизация скорости электропривода при изменении нагрузки.

Подводя итог вышесказанному, сделаем обобщающие выводы:

1) Двукратные САР скорости обладают астатизмом первого порядка как по задающему, так и по возмущающему воздействиям и поэтому относятся к классу астатических САР.

2) Более простую реализацию имеют однократные САР (регулятор скорости пропорциональный, нет входного фильтра).

3) Более быструю реакцию на задающее воздействие имеют также однократные САР.

4) Более благоприятную реакцию на возмущающее воздействие имеют двукратные САР (установившееся падение скорости равно нулю). Однако это достигается за счет значительного (примерно полуторократного) перерегулирования момента и тока якоря двигателя.

Исходя из этих свойств, определяется выбор структуры (однократной или двукратной) в зависимости от конкретных требований к электроприводу, а также с учётом некоторых дополнительных оценок.

4.7. Примеры решения задач

Задача 1. Для двухконтурной системы электропривода нажимных устройств, выполненного на базе двигателя постоянного тока типа ДП-41 и содержащего тиристорный преобразователь с трехфазной мостовой схемой выпрямления выполнить расчет параметров регулятора тока внутреннего контура. Параметры двигателя: Р_ном = 22 кВт; I_ном = 114 А; U_ном = 220 В; r_д = 0.072 Ом; ω_ном = 121.4 с^-1. Параметры преобразователя: U_do = 230 В; I_dном = 160 А; k_п = 13.9; фазное напряжение вторичной обмотки преобразовательного трансформатора U_2ф = 99 В; ток вторичной обмотки трансформатора I_2ф = 136 А; напряжение короткого замыкания трансформатора u_к = 5.5 %. Коэффициент передачи датчика тока k_дт =0.033 В/А.

Решение. Прежде чем приступить к расчету параметров регулятора тока согласно выражения (4.26*) выполним ряд вспомогательных расчетов.

Постоянная времени якорной цепи Т_я = L_я/r_я,

где L_я = L_д + L_п - индуктивность якорной цепи.

Индуктивность двигателя рассчитывают по формуле Уманского

,

где С – постоянная равная 1-1,25 для компенсированных машин; n_ном- номинальная скорость двигателя; р – число пар полюсов.

.

Индуктивность преобразователя определяют как L_п = L_т + L_др,

где L_т – индуктивность трансформатора, приведенная к цепи выпрямленного тока и определяемая как ;L_др – индуктивность сглаживающего дросселя.

.

Поскольку в условиях задачи параметры сглаживающего дросселя не указаны, то его индуктивность не учитываем.

L_я = 9,98*10^-4 + 6,4*10^-3 = 7,4*10^-3 Гн.

Сопротивление якорной цепи определяют как r_я = r_д + r_п ,

где r_п = r_т + r_х – эквивалентное активное сопротивление преобразователя; r_т – активное сопротивление обмоток трансформатора, приведенное к цепи выпрямленного тока; r_т = (0,1- 0,2) ;m – число пульсаций выпрямленного тока; r_х – фиктивное сопротивление, обусловленное коммутационным перекрытием анодных токов

.

r_т = Ом;

r_x = Ом;

r_я = 0,072 + 0,082 + 0,04 = 0,19 Ом.

Т_я = 0,0074/0,19 = 0,039 с.

В качестве некомпенсируемой малой постоянной времени принимаем суммарное значение постоянных времени преобразователя и фильтра датчика тока.

Постоянная времени преобразователя может быть найдена по выражению == 0,0017 с, а постоянную времени фильтра датчика тока находят, исходя из условия подавления пульсаций тока0,006 с.

Тогда Т_μ = 0,0017 +0,006 = 0,0077 с.

= = 0,035;

= = 1,13 с.

Если реализацию регулятора тока выполнять на базе операционного усилителя в виде схемы, показанной на рис. 4.27, то параметры схемы определяются следующим образом. Задавшись желаемой величиной С_о, например 1,0 мкф, находим

r_о = Т_рт / С_о = 1,13/ 10^-6 = 1,13 мОм =1,1 мОм. Величина сопротивлений входной цепи усилителя определится как: r_зт = r_т = r_о /k_рт = 1,1*10⁶ /0,035 = 31 мОм

Задача 2. Для выше приведенной двухконтурной системы подчиненного регулирования, работающей в режиме стабилизации скорости, найти оптимальные параметры регулятора скорости. Момент инерции привода считать равным J = 49,29 кгм²; коэффициент передачи обратной связи по скорости k_c = 0,083 Вс.

Решение. В соответствии с требованиями задания настройку регулятора скорости необходимо производить на модульный оптимум. Тогда согласно разделу 4.4 передаточная функция регулятора скорости будет иметь вид

или в размерных величинах:

R_ω (p) = К_р.с = Jk_д.т/ (4Т_μ СФ k_д.с ).

,

где

Для проверки правильности рассчитанных параметров выполним моделирование рассматриваемой системы регулирования с помощью программы PSM.

Результаты моделирования показаны на рис. 4.28 и рис. 4.29, причем рис. 4.28 отражает изменения тока и скорости на скачок управляющего воздействия, а рис. 4.29 на скачок момента на валу двигателя.

Рис. 4.28. Графики изменения скорости и тока (реакция системы

на скачок управляющего воздействия) при моделировании системы

Рис. 4.29. Графики изменения скорости и тока (реакция системы

на скачок изменения момента на валу двигателя) при моделировании системы