Лабораторная работа № мбф-8 рентгеновская компьютерная томография

Приборы и принадлежности: рентгеновский аппарат и блок компьютерной томографии LEYBOLD DIDACТIC (Германия); персональный компьютер; образцы.

Слово «томография» происходит от греческих слов τομη – сечение и γραφω – пишу, т.е. «пишу по сечениям». Задачей томографии является неразрушающее послойное исследование внутренней структуры объекта. Метод компьютерной томографии был предложен в 1972 году Годфри Хаунсфилдом и Алланом Кормаком, удостоенными за эту разработку Нобелевской премии по физиологии и медицине 1979 года. Метод основан на измерении и сложной компьютерной обработке разности ослабления рентгеновского излучения различными по плотности тканями изучаемого объекта.

Цель работы:

1. изучить теоретические основы рентгеновской компьютерной томографии (РКТ),

2. получить трехмерное изображение исследуемого объекта – сублимированной лягушки (либо детали от конструктора LEGO),

3. определить размеры скелетных костей лягушки,

4. определить линейные коэффициенты ослабления рентгеновских лучей и числа Хаунсфилда различных биологических тканей лягушки.

Рентгеновская компьютерная томография (РКТ) – метод послойного исследования внутренней структуры объекта с помощью рентгеновского излучения. В отличие от обычных рентгеновских снимков, отражающих проекции перекрывающихся структур, при РКТ формируется изображение дискретных срезов объекта, лежащих на различной глубине. РКТ заключается в измерении пространственного распределения коэффициента ослабления рентгеновских лучей веществом и расчете на основе этих данных послойных изображений, свободных от теневых наложений. Объект исследования может быть представлен в виде совокупности конечного числа слоев определенной толщины. Каждая томограмма несет информацию о структуре одного слоя, а каждый слой есть совокупность конечного числа объемных элементов. Значение измеряемого коэффициента ослабления характеризующего эти объемные элементы, присваиваются элементам двумерной матрицы, которая и формирует КТ-изображение.

В самом простом случае, если ослабляющая среда однородна, а рентгеновское излучение монохроматическое, то ослабление его происходит по экспоненциальному закону:

,

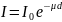где d - толщина слоя вещества, I₀ - интенсивность падающего на образец рентгеновского пучка, I – интенсивность ослабленного пучка, 𝝁 – коэффициент линейного ослабления материала.

Величину ослабления рентгеновских лучей слоем однородного вещества толщиной d называют проекцией или проекционным числом: .

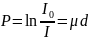Для определения коэффициента ослабления достаточно одного измерения и его значение равно: .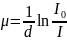

В действительности ослабляющая среда неоднородна (рис.2,б). Каждый объемный элемент объекта – воксел (volume element, вокселы являются аналогами двумерных пикселов для трёхмерного пространства) - имеет собственное значение коэффициента ослабления. В результате одного измерения можно получить только суммарный коэффициент ослабления рентгеновского излучения всеми объемными элементами, расположенными по ходу пучка рентгеновских лучей:

;

,

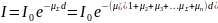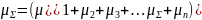d – толщина образца в направлении рентгеновского пучка.

Для определения коэффициентов ослабления каждого элемента одного измерения у же недостаточно.

В общем случае коэффициент ослабления является функцией трех пространственных координат (x, y, z), энергии рентгеновских лучей (так как в действительности рентгеновское излучение не монохроматическое), а в некоторых случаях и времени t (для биологических объектов): μ =μ (x, y, z, Е, t).

Для определения пространственного распределения коэффициента ослабления μ одного измерения недостаточно. Требуется провести множество измерений в разных направлениях (рис. 2, в). Данные этих измерений подвергаются сложной вычислительной обработке.

Существует 2 способа расчета томографических изображений: алгебраический и аналитический. Алгебраические алгоритмы заключаются в построении системы уравнений, в которой неизвестными являются искомые значения коэффициентов ослабления. Например, для нахождения коэффициентов ослабления 4-х объемных элементов (рис.3, а) требуется решить систему из 4-х уравнений с 4 неизвестными.

Для современных матриц реконструкции, состоящих из 1024х1024 или 512х512 элементов (пикселей), такие алгоритмы слишком громоздки. Вместо них применяют аналитические алгоритмы расчета. В них предполагается, что распределение изучаемого параметра описывается непрерывной функцией. Такая модель позволяет сформулировать задачу реконструкции изображений в виде интегрального уравнения относительно неизвестной функции. При этом информация о неизвестном распределении коэффициента о слабления представлена в виде набора проекционных чисел и с математической точки зрения представляет собой преобразование Радона от искомой функции.

Рассмотрим двумерное преобразование Радона (рис.3, б). Пусть в плоскости (х, у) дана двумерная функция f (х, у) (это может быть коэффициент ослабления μ (х, у)). Любая прямая L на плоскости (х, у) может быть задана следующим выражением:

,

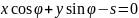где s – расстояние от начала координат до этой прямой, φ – угол между осью х и перпендикуляром, опущенным на прямую из начала координат. Тогда результат интегрирования функции f (х, у) вдоль прямой L зависит от s и φ и имеет вид:

где δ – дельта-функция Дирака. Такое выражение и называется двумерным преобразованием Радона. Чтобы найти f (х, у), нужно выполнить обратное преобразование. Существуют различные алгоритмы восстановления этой функции.

После определения коэффициента ослабления каждого воксела, эти значения преобразуются в специальную цифровую шкалу, в КТ-числа, единицы Хаунсфилда. Визуальным отражением этой шкалы на мониторе аппарата является чёрно-белый спектр изображения. Таким образом, каждому вокселу на изображении соответствует отдельный пиксел, яркость которого отражает ослабление рентгеновского излучения данным вокселем.

Единицы Хаунсфилда используются для количественной, визуальной оценки плотности структур организма. Диапазон единиц шкалы («денситометрических показателей, HU»), соответствующих степени ослабления рентгеновского излучения анатомическими структурами организма, составляет от -1024 HU до +3071 HU, т. е. 4096 чисел ослабления. Средний показатель в шкале Хаунсфилда (0 HU) соответствует плотности воды и эквивалентным ей по ослаблению тканям, отрицательные величины шкалы соответствуют воздуху и жировой ткани, положительные — мягким тканям, костной ткани и более плотному веществу (например, металл). Одна единица шкалы Хаунсфилда соответствует 0,1% разницы ослабления излучения между водой и воздухом, или примерно 0,1% коэффициента ослабления воды, т.к. коэффициент ослабления воздуха практически равен 0.

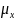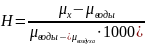Соотношение между коэффициентом линейного ослабления материала и соответствующей единицей Хаунсфилда H имеет вид: . Воздуху присваивают значение H = -1000 НU, так как с хорошим приближением μ_{воздуха}=0. Различным биологическим тканям в нормальном состоянии характерны определенные диапазоны единиц Хаунсфилда H, КТ-чисел. Отличие от этих значений свидетельствует о наличие патологического процесса.

Таблица. Плотность различных тканей в единицах Хаунсфилда.

Интерпретация КТ-числа в большинстве случаев однозначна: более высокие КТ-числа соответствуют тканям с большим значением плотности, а зависимость КТ-числа от плотности выражается линейной функцией. При этом не учитывается зависимость коэффициента ослабления от структуры самого ослабляющего вещества. Речь идет в первую очередь об атомном номере и химической структуре вещества. Оценка таких зависимостей для биологических объектов не представляется возможной в силу чрезвычайно сложного строения макромолекулярных комплексов, из которых они состоят. Чтобы такими зависимостями можно было пренебречь, в клинической компьютерной томографии применяют рентгеновское излучение большой мощности. (Рентгеновские трубки в современных КТ-системах имеют мощность 20-60 кВт при напряжении 80-140 кВ).

Компьютерная обработка изображения позволяет различать более ста степеней изменения плотности исследуемых тканей, что дает возможность дифференцировать различия нормальных и патологических участков тканей в пределах 0,5-1%, т.е. в 20-30 раз больше, чем на обычных рентгенограммах.