5. Как ведут себя стержни прямоугольного поперечного сечения при кручении?

Упомянутые допущения, сформулированные для круглого вала, не могут быть приняты для стержня прямоугольного поперечного сечения.При кручении такого стержня отдельные точки поперечного сечения перемещаются вдоль его оси, и все сечение, в целом, перестает быть плоским (оно коробится). Происходит так называемаядепланация поперечного сечения стержня.

Эта задача является значительно более сложной по сравнению со случаем стержня круглого поперечного сеченияи методами сопротивления материалов она не может быть решена.

6. Какая зависимость существует между углом сдвига и относительным углом закручивания?

Рассмотрим часть вала длиной . Предположим, что правое поперечное сечение вала провернулось на уголотносительно левого сечения. Для произвольного продольного волокна, отстоящего от оси вала на расстоянии, возникнет абсолютный сдвиг, равный(рис. 5.1).

Т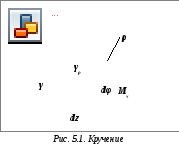огда угол сдвига

. (5.2)

Входящая в формулу (5.2) величина

называется относительным углом закручивания.

Таким образом, между углом сдвига и относительным углом закручивания существует следующая зависимость:

. (5.3)

7. Как записывается закон Гука при кручении?

Так же, как и при сдвиге:

,

или, с учетом зависимости (5.3),

, (5.4)

то есть, касательные напряжения в произвольной точке поперечного сечения вала, отстоящей от центра тяжести на расстоянии , пропорциональны относительному углу закручивания.

При этом в точках, равноудаленных от центра тяжести поперечного сечения, численные значениякасательных напряжений одинаковы.

Из формулы (5.4) следует, что касательные напряжения в поперечном сечении вала изменяются по линейному закону (пропорционально расстоянию от точки до центра тяжести).Они равны нулю в центре вала и достигают максимального значения в точках контура поперечного сечения (рис. 5.2).

Из рис. 5.2 видно, что средняя часть поперечного сечения вала практически не участвует в сопротивлении кручению. В связи с этим на практике находят широкое применение полыевалы. Такие валы, при той же площади поперечного сеченияF, могут воспринять больший скручивающий момент.

8. Как выражается крутящий момент через касательные напряжения, возникающие в поперечном сечении вала?

При повороте поперечного сечения каждая его точка (кроме, разумеется, точки, лежащей на оси вала) перемещается по некоторой дуге окружности радиуса . Поэтому направление касательного напряжения, возникающего в этой точке, должно бытьперпендикулярнок радиусу, проведенному в эту точку.

Элементарная внутренняя сила, возникающая на площадке (см. рис. 5.2), равна, а ее момент относительно оси(или центра тяжести поперечного сечения вала):

.

Суммируя эти элементарные моменты по всей площади, получим выражение для крутящего момента, возникающего в поперечном сечении вала:

. (5.5)

9. Какая зависимость существует между относительным углом закручивания и крутящим моментом?

Подставив выражение (5.4) в формулу (5.5), найдем:

. (5.6)

С учетом того, что интеграл в выражении (5.6) представляет собой полярный момент инерциипоперечного сечения (см. формулу (4.6)), получим иную форму записизаконаГука при кручении вала:

,

где для стержня круглого поперечного сечения

.

Тогда относительный угол закручивания равен:

. (5.7)

Из формулы (5.7) следует, что произведение характеризуетжесткость стержня при кручении. Напомним, чтомодуль сдвига характеризуетжесткость материала при сдвиге (кручении).