14. Какие балки называются статически неопределимыми?

Балки, для которых не удается определить все опорные реакции из уравнений статики, называются статически неопределимыми.

В дальнейшем мы еще вернемся этому вопросу и остановимся на нем подробнее.

15. С какой целью строятся эпюры перерезывающих сил и изгибающих моментов?

Они строятся для наглядного представления о характере изменения этих внутренних силовых факторов по длине балки, а также с целью определения тех опасныхсечений, в которых возникаютнаибольшиекасательные и нормальные напряжения.

Еще раз напомним, что:

1. перерезывающая сила численно равнаалгебраической сумме всех внешних сил (активных и реактивных), действующих на рассматриваемую нами часть балки;

2. изгибающий момент численно равеналгебраической сумме моментов этих же сил относительно главной центральной оси, проходящей через центр тяжести рассматриваемого поперечного сечения (иногда говорят просто – относительно самого сечения).

16. Какие правила знаков используются для вычисления перерезывающей силы и изгибающего момента?

Эти правила, довольно непростые для запоминания, формулируются следующим образом.

Для перерезывающей силы:внешняя сила, действующая на рассматриваемую часть балки и стремящаяся повернуть эту часть относительно сечения по ходу часовой стрелки, вызывает в сечении положительную перерезывающую силу. Такая внешняя сила входит в алгебраическую сумму для определения со знаком «плюс»(рис. 7.5, а).

Заметим, что и положительная перерезывающая сила , в свою очередь, тоже «стремится вращать» любую из частей балки по ходу часовой стрелки.

Теперь приведем правило знаков для изгибающего момента: внешняя нагрузка, изгибающая рассматриваемую часть балки выпуклостью вниз, вызывает в сечении положительный изгибающий момент. Поэтому момент, создаваемый такой нагрузкой, входит в алгебраическую сумму для определения со знаком «плюс» (рис. 7.5, б).

Обращаем внимание Читателя на то, что в этом правиле говорится о моменте, который изгибает балку, а не вращает ее.

Из рис. 7.5, бвидно, что положительный изгибающий момент как бы «стремится изогнуть»любуюиз частей балки также выпуклостью вниз.

Для удобства определения знака изгибающего момента рекомендуется поперечное сечение балки мысленно представлять в виде условной жесткой заделки.

17. Какие дифференциальные зависимости существуют между интенсивностью равномерно распределенной нагрузки , перерезывающей силойи изгибающим моментом, и для чего они используются?

Эти зависимости, имеющие вид:

, (7.1)

впервые были установлены в 1852 г. немецким ученым Иоганом Вильгельмом Шведлером (1823 – 1894 гг.). Позднее они были получены и русским ученымДмитрием Ивановичем Журавским (1821 – 1891 гг.). Формулы (7.1) используютсядля контроля правильности построения эпюр и . Очень часто их называют также формуламиШведлера –Журавского.

Необходимо подчеркнуть, что в приведенных формулах распределенная нагрузка qсчитается положительной, если она направлена вниз.

18. Какие правила используются при построении и проверке эпюр и?

Приведем основныеправила, которые вытекают, непосредственно, из метода сечений, а также являются следствием приведенных выше формулШведлера – Журавского. Отметим, чтонекоторыеиз этих правил справедливы только при обходе эпюр и слева направо.

1. Если на некотором участке балки отсутствует распределенная нагрузка (), то эпюра на этом участке представляет собойпрямую,параллельную оси балки(рис. 7.6). Действительно, поскольку, то и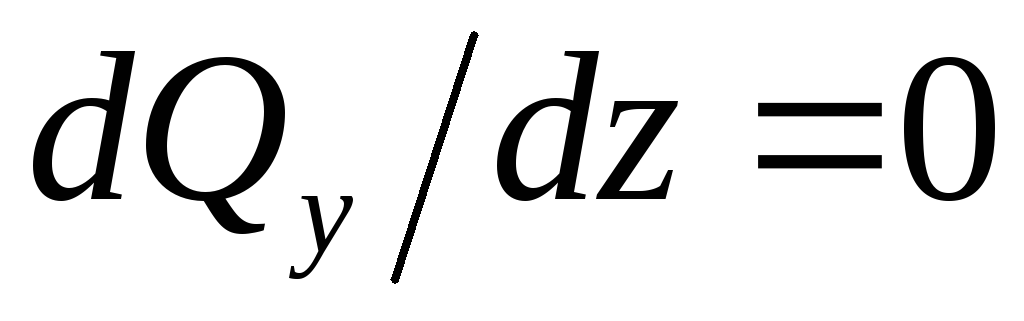. Следовательно,.

Эпюра моментов на этом же участке (где ) – такжепрямая линия. Причем, если, то прямая линия идетвверх, а если, прямая линия идетвниз. Если, то изгибающий моментпостоянен, поскольку.

2. Под сосредоточенной силой Pна эпюре (рис. 7.6,а) имеетсяскачокна величину этой силы и по ее направлению, а на эпюре –излом,уголкоторого всегда направлен навстречу нагрузке.

3. Если на некотором участке балки имеется равномерно распределенная нагрузка, то эпюра на этом участке представляет собойнаклонную прямую (рис. 7.6,б), идущую вниз, если нагрузка направлена вниз, и идущую вверх, если нагрузка направлена вверх. Эпюра на этом участке, согласно третьей формуле (7.1), изменяется по квадратичнойпараболе, причем выпуклость параболы всегда направленанавстречунагрузке.

Если эпюра перерезывающей силы проходит через нулевое значение, то в этом сечении балки на эпюре имеетсяэкстремум(последнее вытекает из зависимости). Отметим, чтов точках, соответствующих началу и концу участка, в пределах которого действует распределенная нагрузка, параболическая и прямолинейная части эпюры переходят одна в другую плавно (без излома).

2. Сосредоточенный внешний момент M(рис. 7.6,в) никак не отражается на эпюре .На эпюре в месте приложения этого момента имеется скачок на его величину.

Заметим, что построение эпюр перерезывающих сил и изгибающих моментов ввел в практику расчета балок на изгиб в 1859 г. французский ученый Жак Антуан Шарль Бресс(1822 – 1883 гг.).