1. Чему равны внутренние усилия и напряжения при внецентренном сжатии?

Пусть сжимающая сила приложена в некоторой точкеAс координатамиив главных центральных осях инерцииx иy (рис. 10.1,а).

Т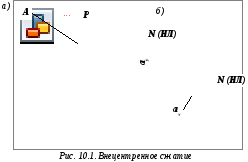огда, с учетом принятого нами допущения,

.

Точныезначения изгибающих моментов определяются по формулам:

,

где ипрогибы рассматриваемого поперечного сечения стержня в направлении осейи, соответственно. Принятое нами выше допущение о большой жесткости стержня на изгиб заключается в предположении, что.

Напряжения в произвольной точке с координатамиибудут равны:

, (10.1)

где, согласно принципу независимости действия сил, первое слагаемое представляет собой напряжение от сжатия, а второе и третье – от изгиба.

Значения изгибающих моментов и координат исследуемой точки подставляются в формулу (10.1) поабсолютномузначению, а знак второго и третьего слагаемых определяется по физическому смыслу.

2. Как определяется положение нулевой линии (нл)?

Преобразуем формулу (10.1), подставляя в нее значения изгибающих моментов:

. (10.2)

Обозначим координаты некоторой точки нулевой линии и. Подставляя эти координаты в (10.2) и учитывая, что напряжения в точкахНЛравны нулю, после сокращения на, получимуравнение НЛ:

. (10.3)

Важно отметить, что НЛ и точка приложения нагрузки всегда расположены по разные стороны от центра тяжести поперечного сечения (см. рис. 10.1,б).

3. Чему равны отрезки, отсекаемые нулевой линией от осей координат?

Эти отрезки, которые мы обозначим через и(см. рис. 10.1,б), легко найти из выражения (10.3). Если сначала в нем принять, а затем –, то мы легко найдем, что отрезки, отсекаемыеНЛ от осей координат, определяются по формулам:

; .

4. Что называется ядром сечения?

Ядром сечения называется малая область вокруг центра тяжести поперечного сечения стержня. Она характеризуется тем, что всякая сжимающая сила, приложенная внутри этой области, вызывает во всех точках поперечного сечения (и, соответственно, во всем стержне) только напряжения сжатия.

Понятие о ядресечениявпервые ввелБрессв 1854 г.

Рассмотрим следующий пример. Пусть стержень имеет прямоугольное поперечное сечение с размерами b иhи одна из координат точки приложения нагрузки (точкаA) равнанулю, например(рис. 10.2). Тогда напряжения в крайних точкахK иL поперечного сечения стержня будут определяться по формулам:

Из этих формул видно, что приво всех точках поперечного сечения и, в частности в крайних точкахK иL, будут возникатьодинаковыесжимающие напряжения. Принапряжения, по-прежнему, будутсжимающими, но будут изменяться по ширине сечения. Прив точкахK иLони будут равны:.

Если , то нулевая линия разделит поперечное сечение на две части. В одной из них напряжения будут сжимающими, а в другой – растягивающими. Для всех этих случаев (см. рис. 10.2) показаны эпюры напряжений.

Таким образом, если мы не хотим, чтобы в поперечном сечении внецентренно сжатого стержня возникали растягивающие напряжения (а многие строительные материалы, как известно, очень плохо работают на растяжение), то эксцентриситет нагрузки не должен выходить за некоторую область вокруг центра тяжести этого сечения. Эту область и называютядром сечения.