1. Что называется статическим моментом площади сечения относительно оси?

Рассмотримпроизвольную плоскую фигуру (поперечное сечение стержня) площадью F. Проведем через произвольную точку О оси координат x и y. Выделим элемент площади с координатамиx и y (рис. 4.1).

П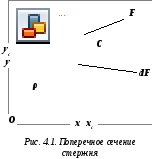о аналогии с понятиеммомента силы относительно оси введем понятие момента (или статического момента) площади фигуры относительно оси.

Величину, равную произведению элемента площади на расстояниеy до оси x, назовем моментом элемента площади относительно оси:

.

Тогда момент элемента площади относительно осиy равен:

.

Просуммировав такие произведения по всей площади F, мы получим, соответственно, моменты площади всей фигуры относительно осей x и y:

. (4.1)

Момент площади фигуры относительно оси измеряется в единицах длины в кубе (как правило, в см³).Он может быть положительным, отрицательным и, как мы увидим в дальнейшем, равным нулю.

Пусть – координаты центра тяжести фигуры. Продолжая аналогию с моментом силы, можно записать следующие выражения:

. (4.2)

Таким образом, статическим моментом (или просто, моментом) площади фигуры относительно оси называется произведение площади фигуры на расстояние от ее центра тяжести до оси.

2. Как определить координаты центра тяжести поперечного сечения стержня?

Из формул (4.2) следует, что статический момент площади фигуры относительно центральной оси (то есть оси, проходящей через центр тяжести фигуры) равен нулю.

Сопоставляя (4.1) и (4.2), мы легко получим формулы, позволяющие определить положение центра тяжести поперечного сечения стержня:

. (4.3)

Если площадь всей фигуры можно разбить на n простых частей, для которых известны и площадь, и положение центра тяжестии, то вместо формулы (4.3) мы получим:

.

3. Что называется осевым, полярным и центробежным моментами инерции фигуры? в каких единицах они измеряются?

Осевым моментом инерции площади фигуры называется интеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси. Так, моменты инерции произвольной фигуры (см. рис. 4.1) относительно осейxи y, соответственно, равны:

. (4.4)

Полярным моментом инерции площади фигуры относительно данной точки (полюса) называется интеграл произведений элементарных площадей на квадраты их расстояний до полюса:

. (4.5)

Если через полюс проходят две взаимно перпендикулярные оси x и y, то . И тогда

.

Из формул (4.4) и (4.5) видно, что значения осевых и полярного моментов инерции всегда положительны, так как координаты и расстояниевходят в них в квадрате.

Центробежным моментом инерции площади фигуры называется интеграл произведений элементарных площадей на их расстояния до осей x и y:

.

Моменты инерции измеряются в единицах длины в четвертой степени (как правило, см⁴).

Понятие момента инерции поперечного сечения ввел в 1834 г. французский инженер Н. Перси.

4. Какие оси называются главными осями?

Взависимости от положения координатных осей центробежный момент инерции может быть положительным, отрицательным, а также равным нулю.Рассмотрим, например, квадрат (рис. 4.2, а).

Центробежный момент инерции квадрата относительно осейположителен, так как координатыу всех элементов площади положительные. При повороте осей вокруг начала координат на угол 90⁰ (рис. 4.2 б) знак центробежного момента инерции становится отрицательным, так как в этом случае координаты x всех элементарных площадей положительны, а координаты y – отрицательны.

Очевидно, что можно найти такое положение двух взаимно перпендикулярных осей , при котором . Такие оси называютсяглавными осями. Для квадрата такие оси изображены на (рис. 4.2, в).

Если фигура имеет ось симметрии, то эта ось является одной из главных осей (другая ось перпендикулярна ей).

Главные оси, проходящие через центр тяжести поперечного сечения стержня, называются главными центральными осями.