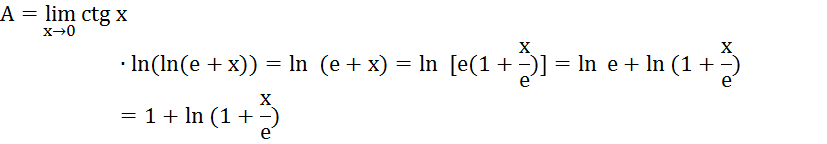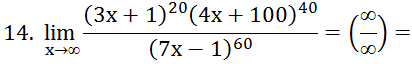Краткое обобщение теорем


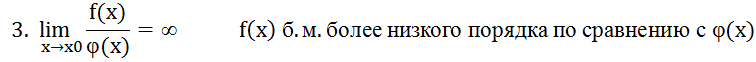
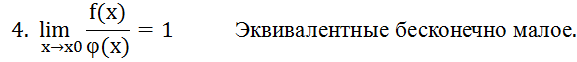 малые
малые
Эквивалентные бесконечно малые


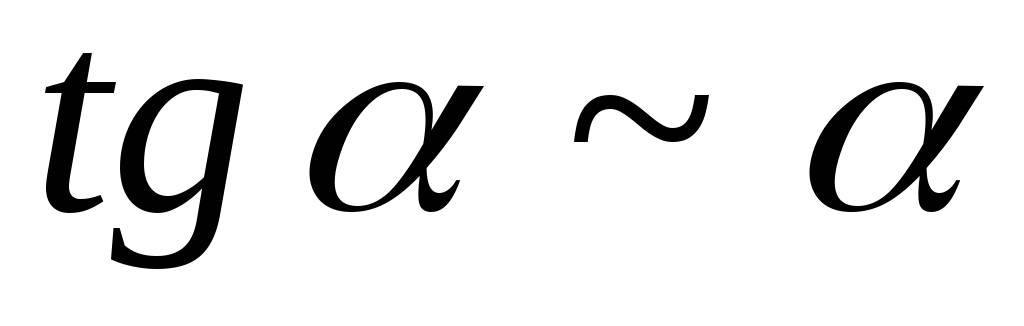
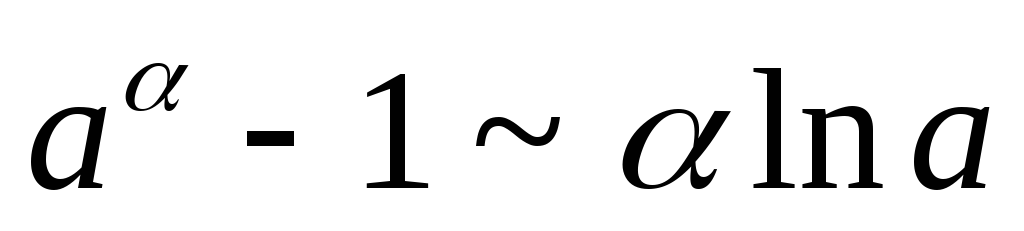






Примеры на применение эквивалентных б.М.
-
Сравнить
функции
а)

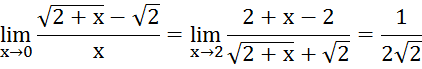
б)
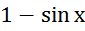 и
и  ,
,

т.е.
 бесконечно малое высшего порядка по
сравнению с
бесконечно малое высшего порядка по
сравнению с 

-
Сравним
функции : 
 при
при 
 , то учитываем, что
, то учитываем, что  при
при 




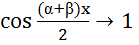

3. Выделим главную
часть функции
 при
при  ,
, 
а) при малых x
поведение функции f(x)
определяет слагаемое, стоящее в низшей
степени. Вынесем за скобки x
.
 выражение в скобках ⟶3
при x⟶0
, следовательно
выражение в скобках ⟶3
при x⟶0
, следовательно 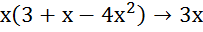 , тогда
, тогда 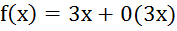 при x⟶0
(читается: 3х + бесконечно малая от 3х)
при x⟶0
(читается: 3х + бесконечно малая от 3х)
 -
главная часть функции f(x)
-
главная часть функции f(x)
 – б.м. более высокого порядка, чем
– б.м. более высокого порядка, чем 
б) 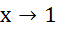 ,
,  Следовательно функция
Следовательно функция  есть б.м. в точке
есть б.м. в точке 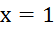
Многочлен  делится на
делится на  . Получаем:
. Получаем:

При 

То  т.е
т.е

 – б.м. более высокого порядка чем
– б.м. более высокого порядка чем 
4. Выделим главную
часть функции  при
при 
Используем
эквивалентное соотношение 

т.к.  при
при 
т.е. 
5. Выделим главную
часть функции  при
при 
т.к выражение,
стоящее под знаком логарифма  при
при  , то
, то 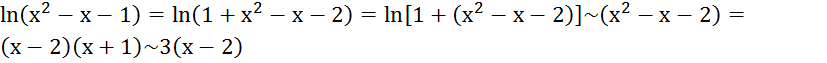 ,
,

Отсюда:

6. Выдели главную
часть функции 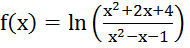 ,
при
,
при 

 при
при
 наибольшая степень
наибольшая степень 

7. Выделим главную
часть
 ,
, 
 ,
,

8. 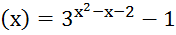 ,
, 

 ,
,



Функция является
б.м. при  .
Найдем главную часть этих функций
.
Найдем главную часть этих функций
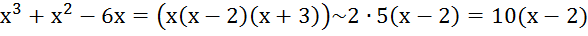 ,
, 





При 
 и
и 
Преобразуем: 


В сумме заменить
б.м. на эквивалентные нельзя, поэтому
перепишем:


14).
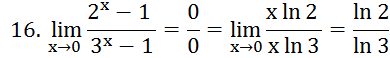
Рассмотрим случаи
неопределенности
 .
.
15).
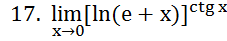

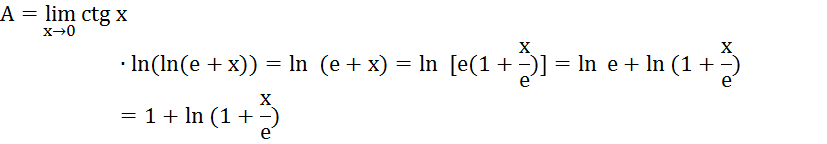
Тогда, при 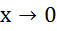



Рассмотрим
отношение бесконечно
больших величин:
16).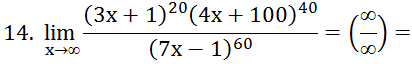




17).
18).



Применение
эквивалентных бесконечно-малых для
нахождения пределов (примеры из
Кузнецова):
19).
20).

21).

Разобьем
вторую скобку на два сомножителя:

1)

14




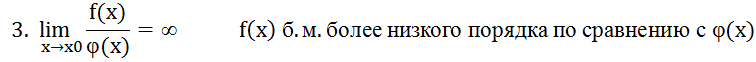
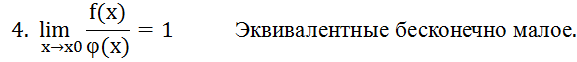 малые
малые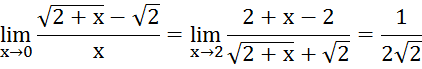



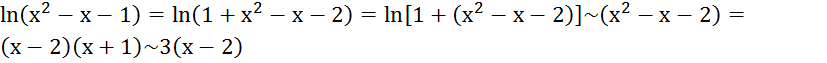 ,
,