Второй замечательный предел
Сначала найдем предел бесконечной последовательности {yn}, где
yn
=
Покажем, что эта последовательность монотонно возрастает и притом ограниченная.
1) Убедимся, что yn+1 > yn при всяком целом положительном n.
По формуле Ньютона для полинома n-ой степени запишем
yn
=
=
+
+
… +
-----------------------------------------------------------------------------------------
= an
+
+
+
… +
Дифференциальный бином
_________________________________________________________________
Разделим каждый сомножитель числителя на n, получим
=
+
+…..
+
,
теперь найдем
=
=
1 + 1 +
+
+ ….
+
+
+
.
В правой части
равенства
имеем одно дополнительное последнее
слагаемое. Кроме того, все слагаемые,
начиная с третьего у
больше соответствующих для
,
т.к.
.
Следовательно,
>
,
т.е. последовательность
монотонно возрастающая.
2) Покажем, что при
всяком целом положительном n,
2 <
< 3.
В равенстве для
члены
суммы, начиная с 3-го слагаемого, больше
нуля, поэтому
>
2. В равенстве для
отбросим
все вычитаемые
<
1 + 1 +
+
+ … +
,
а в знаменателе все цифры (кроме единицы) заменены на 2:
=
;
<
;
<
;
…
<
;
В этом случае правая часть увеличится и будет
=
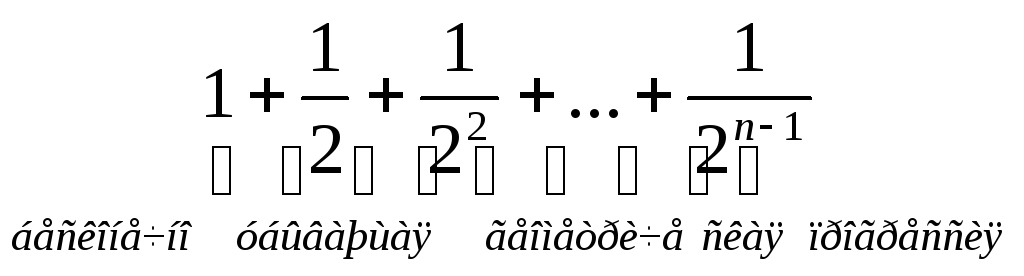< 1 +
Но справа, начиная
со второго члена, убывающая геометрическая
прогрессия со знаменателем q
=
.
Её сумма будет
= 1 +
= 3-
.
Таким образом, при всяком n
2 <
<
3-
.
< 3,
Т.е. последовательность
ограничена
сверху и монотонно возрастает.
Следовательно, последовательность
имеет предел. Этот предел впервые найден
в XVII
столетии Непером, называется неперовым
числом и обозначается буквой е.
=
e.
Число е – иррациональное. Его приближенное значение е = 2.71828.
Можно показать, что к этому же пределу стремится и функция непрерывно изменяющегося аргумента
y
=
,
когда ее аргумент
z
стремится к
.
=
е.
Рассмотрим случай:
z
Для доказательства заключим каждое значение z между двумя последовательными целыми числами
n
z
< n
+ 1. (1)
Если z
,
то одновременно стремится к
и n.
Отсюда находим
или
.
Прибавим единицу
или
.
(2)
Возведем члены неравенства в степени, показателями которых служат члены неравенства (1), тогда
.
(3)
(Знаки неравенства не изменятся, т.к. наименьшее число возводится в наименьшую степень, наибольшее – в наибольшую). По теореме о пределе произведения и частного имеем
=
=
e
1=
e
(4)
=
=
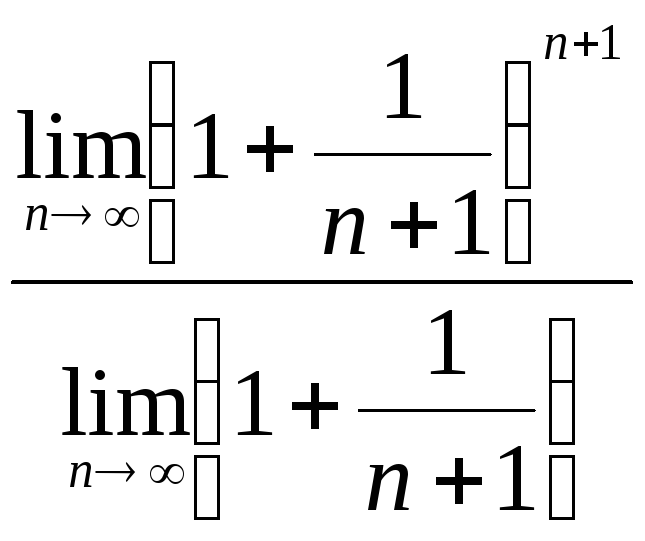= e
. (5)
Т.о. из (4) и (5) видно, что крайние члены неравенства (3) стремятся к одному и тому же пределу – числу е. Поэтому по теореме о «двух милиционерах» имеем
=
е
(6)
Легко показать, что
=
е
(7)
Пусть z
= - u,
тогда при z
-
,
u
,
поэтому
=
.
Сделаем следующие преобразования
=
=
=
=
Тогда,
=
=
=
е.
Если теперь положим
,
то получим значение исходного выражения,
приведенного в начале лекции. Величина,
обратная бесконечности является
бесконечно малой: z
,
х
будет
к 0. Поэтому, заменяя z
на x,
получаем
=
е.
(8)