Вариант 8
О двух акциях А и В известно, что они выпущены одной и той же отраслью. Вероятность того, что акция А поднимется в цене завтра равна 0,2. Вероятность того, что обе акции А и В поднимутся завтра в цене, равна 0,12. Предположим Вы знаете, что акция А поднимется завтра в цене. Чему равна вероятность того, что и В также поднимется в цене?
На химическом заводе установлена система аварийной сигнализации. Когда возникает аварийная ситуация, звуковой сигнал срабатывает с вероятностью 0,95 звуковой сигнал может сработать случайно, без аварийной ситуации с вероятностью 0,02. Реальная вероятность аварийной ситуации равно 0,004. Предположим, что звуковой сигнал сработал. Чему равна вероятность реальной аварийной ситуации.
В билете 4 задачи. Вероятность правильного решения первой задачи равна 0,9; второй – 0,8; третьей – 0,7; четвертой – 0,6. Составить закон распределения СВХ - число правильно решенных задач. Найти F (х); построить ее график. Вычислить Д (х).
Непрерывная СВХ заданы функцией
Найти:
.
Справедливо ли при =0,05 утверждение продюсера, что передачу смотрят 30% телезрителей, если из 400 опрошенных данную передачу смотрело 100 человек?
. На предприятии разработан новый технологический процесс вместо существовавшего, Провели сравнительный анализ существующего и нового технологического процесса по себестоимости продукции. Для этого по существующей технологии изготовлено
изделий, средняя себестоимость которых
тыс
руб.,
,
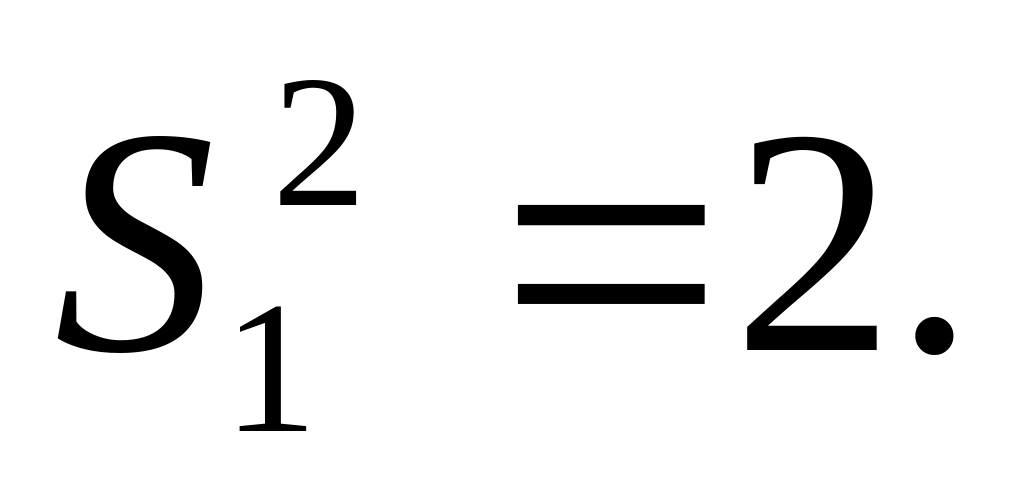а по новой -
,
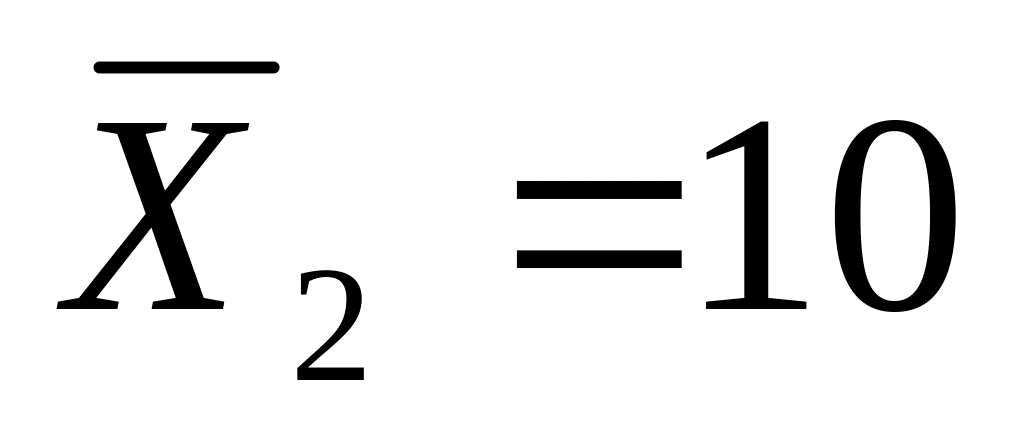тыс руб.,
.
Считаете ли Вы целесообразным при 5%
уровне значимости ввести новую
технологию.
7. Покупатель приобретает большую партию интегральных схем для компьютеров в том случае, если вероятность того, что изделие окажется бракованным не превысит 0,002. Среди отобранных 1000 схем оказалось три бракованных. Можно ли принять партию ? ( = 0,005)
8. Независимые выборки из двух нормально распределенных совокупностей с одинаковым средним квадратичным отклонением дали следующие результаты:
Выборка |
n |
Среднее |
Среднее квадратичное отклонение |
1 |
13 |
22 |
9 |
2 |
9 |
25 |
7 |
Можно ли сделать заключение, что разница между двумя генеральными средними меньше 3? Проверить гипотезу для = 0,05.
9. Имеются следующие данные 25 заводов одной из отраслей промышленности:
№ |
Х |
У |
1 |
0,8 |
0,6 |
2 |
0,9 |
0,6 |
3 |
1 |
1,1 |
4 |
1 |
0,9 |
5 |
1,6 |
1,5 |
6 |
0,5 |
0,4 |
7 |
3,5 |
3 |
8 |
3,9 |
4,2 |
9 |
3,3 |
4,5 |
10 |
3 |
2 |
11 |
3,1 |
4 |
12 |
3,1 |
3,6 |
13 |
2,9 |
3,2 |
14 |
2,7 |
2,3 |
15 |
4,5 |
5,6 |
16 |
5,5 |
8,1 |
17 |
5,1 |
4,2 |
18 |
5,6 |
7,9 |
19 |
4,7 |
4,5 |
20 |
4,9 |
4,4 |
21 |
7 |
3,5 |
22 |
8,1 |
7,6 |
23 |
6,3 |
6 |
24 |
6,6 |
6,5 |
25 |
6,8 |
6,9 |
Требуется:
Построить корреляционное поле.
Найти числовые характеристики ,
Вычислить коэффициент корреляции.
Найти уравнения прямых регрессии у на х и х на у и нанести их графики на корреляционное поле.
Проверить значимость коэффициента корреляции на уровне значимости = 0,01