Вариант 3

1. В круге радиуса R наудачу появляется точка. Найти вероятность того, что она попадет во внутрь вписанного в окружность равнобедренного треугольника с высотой .

2. В двух партиях и % доброкачественных изделий, соответственно наудачу выбирается по одному изделию из каждой партии. Какова вероятность обнаружить среди них а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно бракованное (Вычислить при ).

3. Вероятность «сбоя» в работе телефонной станции при каждом вызове равна р. Поступило n вызовов. Определить вероятность а) m «сбоев»; б) более чем m-3 сбоев.

M = 7; n = 1000; р = 0,009.

4. Плотность распределения вероятностей случайной величины имеет вид Найти , М (х), Д (х), F (х);

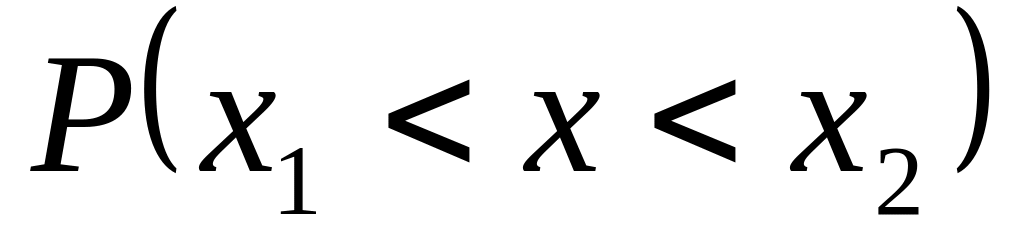
= -2, = 8, с = -2,

5. Согласно рекламе применение удобрения повышает урожайность пшеницы не менее, чем на 4 ц/га. Удобрения вносили в почву на 17 гектарах, в результате чего был получен урожай в среднем только на 3,5 ц/га выше при S=1 ц/га. Проверить на 5% уровне значимости достоверность рекламы.

6. Средний объем для 10 торговых точек одного района составляет 4 млн. руб. при =1, а для 8 торговых точек другого района – 5 млн. руб. и = 2. Можно ли утверждать при 5% уровне значимости, что второй район предпочтительней первого.

7. Из продукции первой смены отобрано = 200 деталей, а из второй = 100. Из отобранных деталей дефектными оказались соответственно =30 и =12. Определите при = 0,05 различается ли продукция этих смен по доле дефектных изделий.

8. На основании 18 наблюдений установлено, что на 64% вес (Х) кондитерских изделий зависит от их объема (У). Можно ли на уровне значимости =0,05 утверждать, что между Х и У существует зависимость.

9. Даны результаты испытания прибора на продолжительность работы Т (ч.).

Требуется:

1. Составить интервальный статистический ряд.

2. Построить полигон и гистограмму распределения.

3. Подобрать закон распределения испытуемой СВ.

4. Найти точечные оценки параметров распределения.

5. Проверить на уровне значимости = 0,05 гипотезу о выдвинутом законе распределения

3200	0	128	240	800	1120	1140	25	900	2000	0	24	900
1300	2500	0	700	500	1500	1900	1920	75	180	800	7	1400
440	520	901	1810	27	5	2200	450	810	1300	15	150	803
48	543	525	1240	990	800	413	700	511	630	241	25	1100
1320	76	811	0	1125	99	2500	2300	79	1600	24	1800	3
2800	2100	1700	1700	900	550	500	400	1000	24	963	741	0
0	700	1320	1410	140	1970	511	1310	1370	500	84	120	24
2530	0	3500	810	800	910	75	1120	123