
- •Российский экономический университет им. Г.В. Плеханова
- •Часть II
- •Российский экономический университет
- •Часть II
- •Содержание
- •Раздел I. Линейная алгебра.
- •Раздел II. Аналитическая геометрия.
- •Раздел III. Теория вероятностей.
- •Раздел 1. Линейная алгебра.
- •Система линейных уравнений. Метод Гаусса.
- •Арифметическое векторное пространство.
- •1.3. Матрицы.
- •Определители.
- •Раздел II. Аналитическая геометрия.
- •2.1. Скалярное и векторное произведения векторов.
- •2.2. Прямая на плоскости.
- •2.3. Плоскость.
- •2.4. Прямая в пространстве.
- •Раздел III. Теория вероятностей.
- •3.1. Элементы комбинаторики: сочетания, размещения, перестановки.
- •3.2. Понятие случайного события. Классическое определение вероятности события.
- •3.3. Операции над событиями. Условная вероятность. Теоремы сложения и умножения вероятностей.
- •3.4. Формула полной вероятности. Формула Бейеса.
- •3.5. Формула Бернулли. Теорема Пуассона. Локальная и интегральная теоремы Лапласа.
- •3.6. Закон распределения, функция распределения и числовые характеристики дискретной случайной величины (дсв). Законы распределения: биноминальный, Пуассона.
- •3.7. Плотность распределения, функция распределения и числовые характеристики непрерывной случайной величины (нвс). Нормальное распределение.
- •3.8. Законы распределения и числовые характеристики случайных векторов.
- •Раздел I.
- •Раздел II.
- •Раздел III.
Определители.
.
Вычислить определитель:
а)
![]() ; б)
; б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ; е)
; е)
![]() ;
;
ж) ;
з)
;
з)
 ;
и)
;
и)
![]() ;
;
к)
![]() .
.
Вычислить определитель:
а)
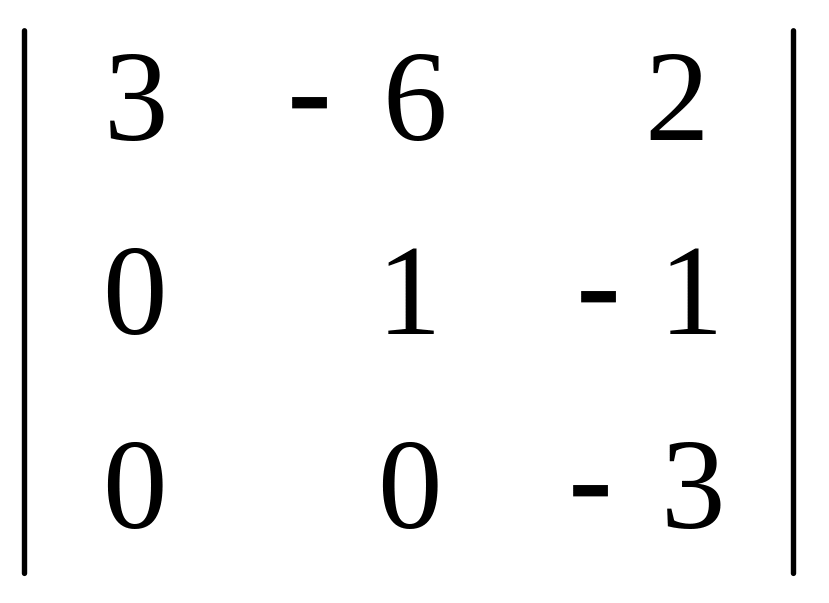 ; б)
; б)
 ;
в)
;
в)
 ;
;
г)
 ; д)
; д)
 ; е)
; е)
 ;
;
ж)
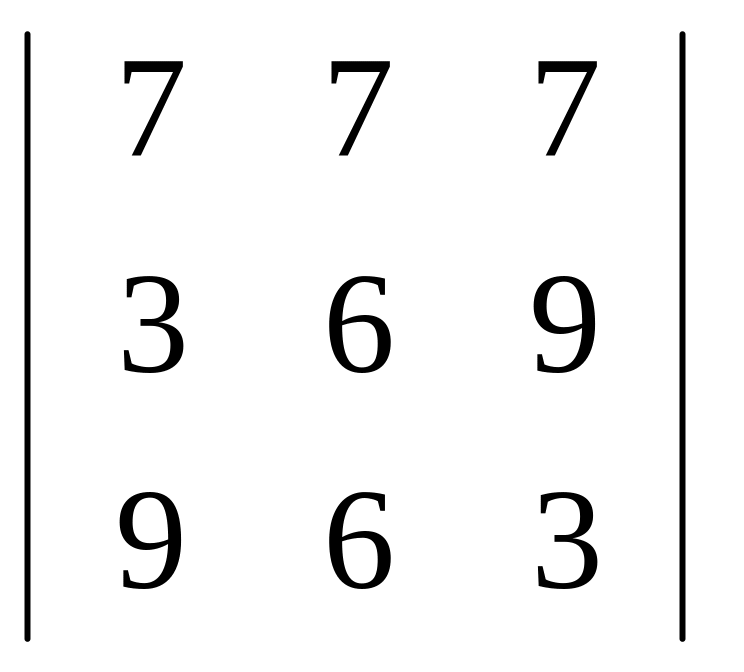 ;
з)
;
з)
 ;
и)
;
и)
 ;
;
к)
 ; л)
; л)
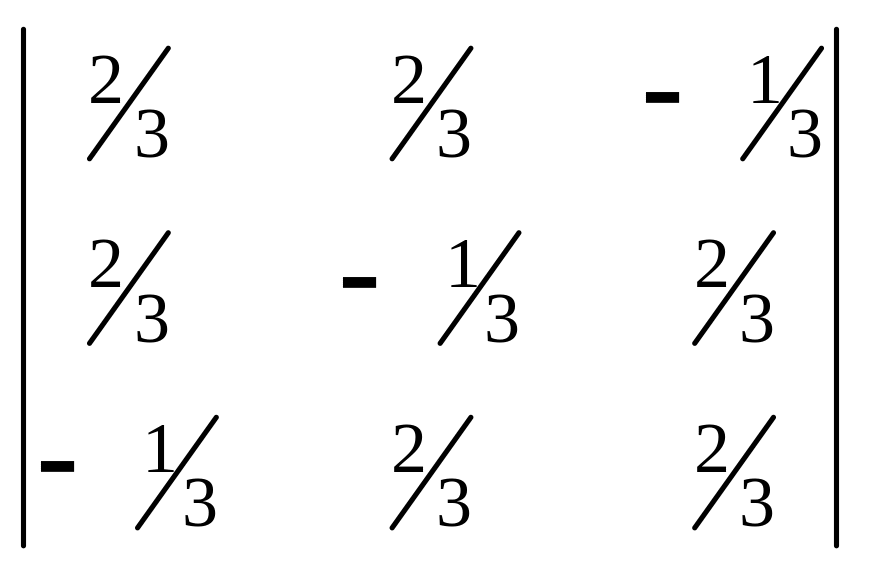 .
.
Вычислить определитель:
а)
 ; б)
; б)
 ;
в)
;
в)
 ;
;
г)
 ; д)
; д)
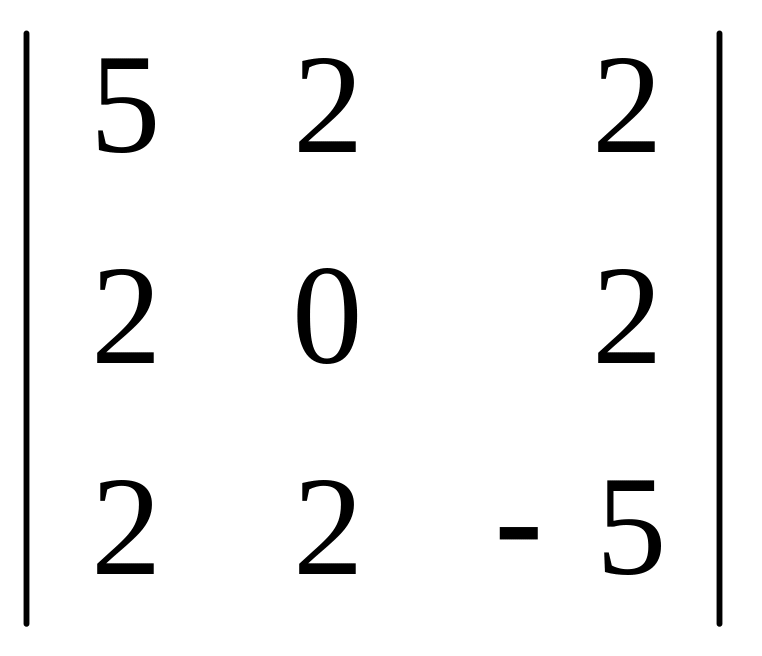 ;
е)
;
е)
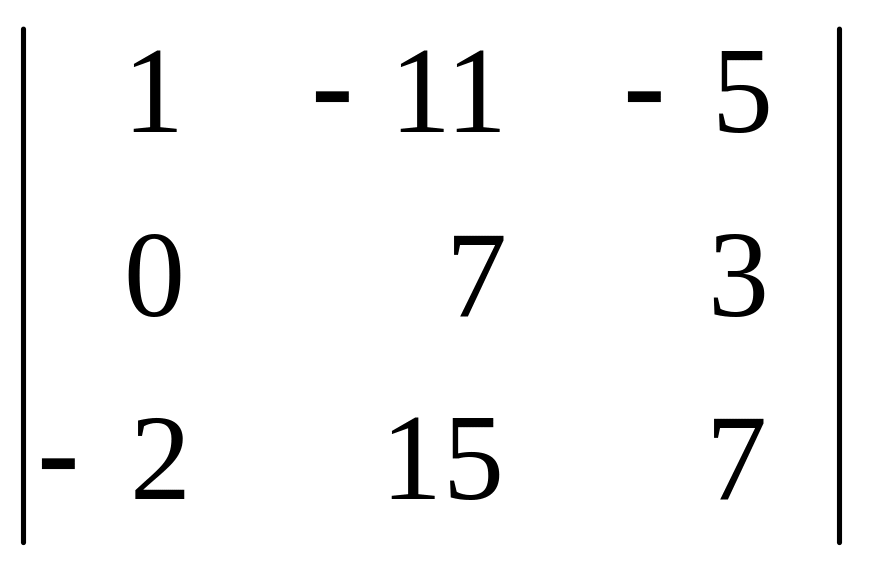 ;
;
ж)
 ;
з)
;
з)
 ;
и)
;
и)
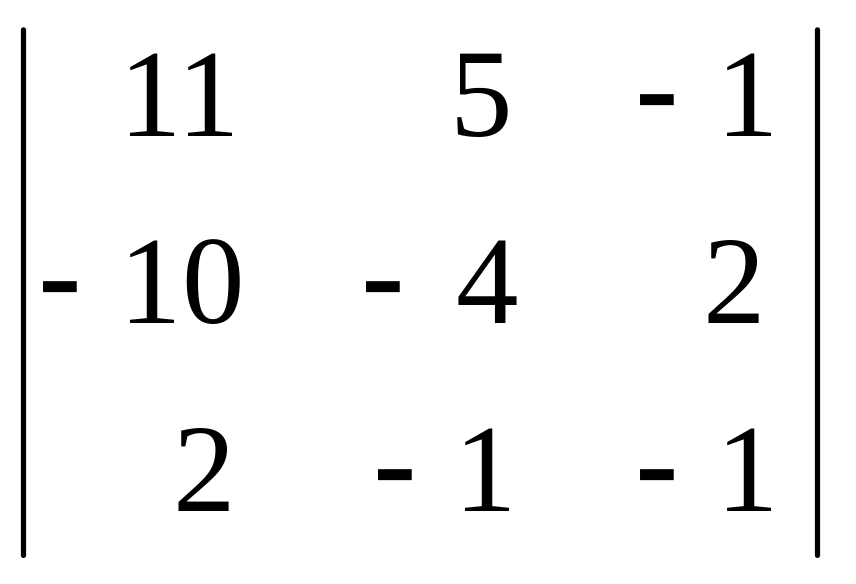 .
.
Вычислить определитель:
а)
 ; б)
; б)
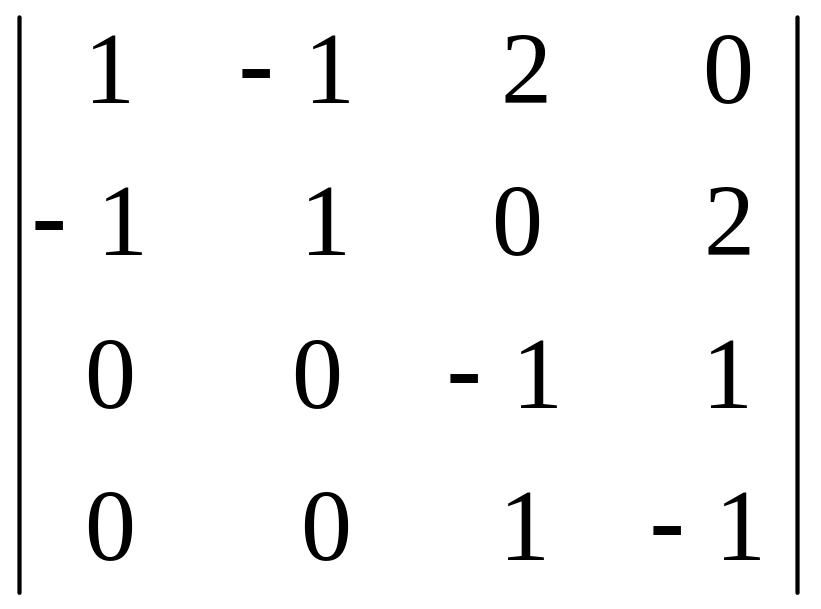 ;
в)
;
в)
 ;
;
г)
 ; д)
; д)
 ; е)
; е)
 ;
;
ж)
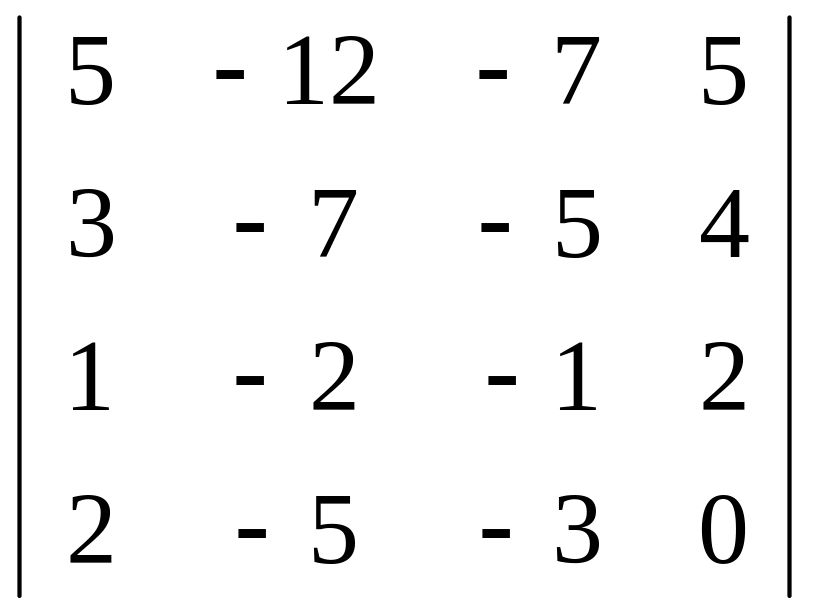 ;
з)
;
з)
 ;
и)
;
и)
 ;
;
к)
 .
.
Пользуясь правилом Крамера, решить систему уравнений:
а)
![]() ; б)
; б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ;
з)
;
з)
![]() ;
и)
;
и)
![]() ;
;
к)
![]() .
.
Пользуясь правилом Крамера, решить систему уравнений:
а)
 ;
б)
;
б)
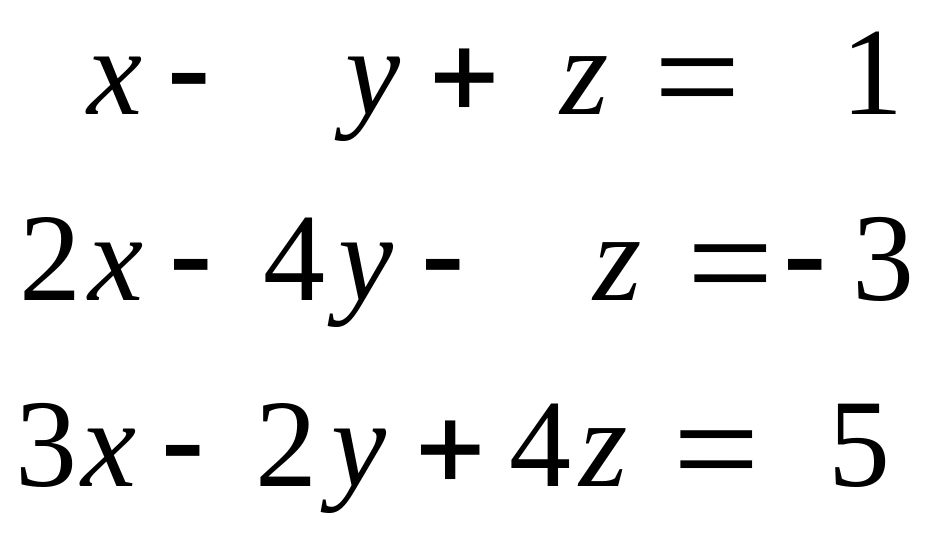 ;
в)
;
в)
 ;
;
г)
 ;
д)
;
д)
 ;
е)
;
е)
 ;
;
ж)
 ;
з)
;
з)
 ;
;
и)
 ;
к)
;
к)
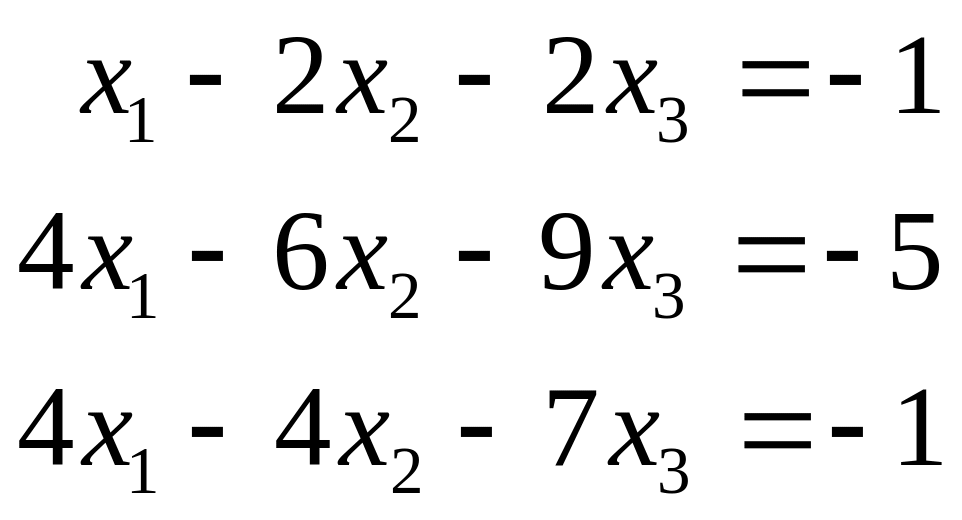 .
.
Раздел II. Аналитическая геометрия.
2.1. Скалярное и векторное произведения векторов.
2.1.1.
Векторы a
и b образуют
угол /6,
а
= 2 и b
= 5. Найти
![]() (a,
b).
(a,
b).
2.1.2. Векторы a и b образуют угол /4, а = 4 и b = 3. Найти (a, b).
2.1.3. Векторы a и b образуют угол 2/3, а = 3 и b = 2. Найти (a, b).
2.1.4.
Векторы a
и b образуют
угол /6,
а
= 2 и b
= 1. Найти
![]() (2a
– 3b,
4a
+ 2b).
(2a
– 3b,
4a
+ 2b).
2.1.5. Векторы a и b образуют угол /4, а = 4 и b = 3. Найти (2a – 3b, a + 2b).
2.1.6. Векторы a и b образуют угол 2/3, а = 3 и b = 2. Найти (a – 3b, 4a + 2b).
2.1.7. Найти скалярное произведение векторов a = {1;2;-1} и b = {2,0,3}.
2.1.8. Найти скалярное произведение векторов a = {3;2;-4} и b = {2,1,3}.
2.1.9. Даны векторы a = {1;2;-2} и b = {4,0,3}. Найти (a – 3b, 4a + 2b).
2.1.10. Даны векторы a = {2;2;-1} и b = {0,5,-12}. Найти (2a – b, 3a + 2b).
2.1.11. Найти косинус угла между векторами a = {1;1;0} и b = {1,0,1}.
2.1.12. Найти косинус угла между векторами a = {1;2;3} и b = {6,4,-2}.
2.1.13. Даны точки A = (-1; -2; 4), B = (-4, -2,0), C = (3, -2,1). Найти косинус внутреннего угла треугольника ABC при вершине B.
2.1.14. Даны точки A = (3; 2; -3), B = (5, 1, -1), C = (1, -2, 1). Найти косинус внешнего угла треугольника ABC при вершине A.
2.1.15. Даны векторы a = {3;-1;-2} и b = {1,2,-1}. Найти [2a – b, 2a + b].
2.1.16. Даны векторы a = {2;2;-1} и b = {0,5,-12}. Найти [2a + b, 3a + 2b].
2.1.17. Даны точки A = (1; -1; 2), B = (5, -6,2), C = (1,3, -1). Найти площадь треугольника ABC и длину высоты этого треугольника, опущенной из вершины B.
2.1.18. Даны точки A = (1; 2; 0), B = (3,0, -3), C = (5,2,6). Найти площадь треугольника ABC и длину высоты этого треугольника, опущенной из вершины A.
2.1.19. Параллельны ли векторы a = {2;-1;1}, b = {1;-1;2}, c = {3;-2;3} одной плоскости?
2.1.20. Параллельны ли векторы a = {3;0;1}, b = {2;1;3}, c = {5;1;1} одной плоскости?
2.1.21. Лежат ли точки A = (0;0;0), B = (1;-1;2), C = (1;1;3), D = (2;0;5) в одной плоскости?
2.1.22. Лежат ли точки A = (1;1;1), B = (2;1;1), C = (1;2;1), D = (1;1;2) в одной плоскости?
2.1.23. Даны точки A = (1;-1;2), B = (5;-6;2), C = (1;3;-1), D = (2;-1;2). Найти объем тетраэдра ABCD и длину высоты этого тетраэдра, опущенной из вершины D.
2.1.24. Даны точки A = (1;2;0), B = (3;0;-3), C = (5;2;6), D = (1;2;1). Найти объем тетраэдра ABCD и длину высоты этого тетраэдра, опущенной из вершины D.
