
- •Российский экономический университет им. Г.В. Плеханова
- •Часть II
- •Российский экономический университет
- •Часть II
- •Содержание
- •Раздел I. Линейная алгебра.
- •Раздел II. Аналитическая геометрия.
- •Раздел III. Теория вероятностей.
- •Раздел 1. Линейная алгебра.
- •Система линейных уравнений. Метод Гаусса.
- •Арифметическое векторное пространство.
- •1.3. Матрицы.
- •Определители.
- •Раздел II. Аналитическая геометрия.
- •2.1. Скалярное и векторное произведения векторов.
- •2.2. Прямая на плоскости.
- •2.3. Плоскость.
- •2.4. Прямая в пространстве.
- •Раздел III. Теория вероятностей.
- •3.1. Элементы комбинаторики: сочетания, размещения, перестановки.
- •3.2. Понятие случайного события. Классическое определение вероятности события.
- •3.3. Операции над событиями. Условная вероятность. Теоремы сложения и умножения вероятностей.
- •3.4. Формула полной вероятности. Формула Бейеса.
- •3.5. Формула Бернулли. Теорема Пуассона. Локальная и интегральная теоремы Лапласа.
- •3.6. Закон распределения, функция распределения и числовые характеристики дискретной случайной величины (дсв). Законы распределения: биноминальный, Пуассона.
- •3.7. Плотность распределения, функция распределения и числовые характеристики непрерывной случайной величины (нвс). Нормальное распределение.
- •3.8. Законы распределения и числовые характеристики случайных векторов.
- •Раздел I.
- •Раздел II.
- •Раздел III.
Раздел II.
2.1
2.1.1.
5![]() .
2.1.2.
6
.
2.1.2.
6![]() .
2.1.3.
–3. 2.1.4.
26 – 8
.
2.1.5.
– 22. 2.1.6.
–42. 2.1.7.
–1. 2.1.8.
–4. 2.1.9.
–94. 2.1.10.
–262. 2.1.11.
1/2. 2.1.12.
2/7. 2.1.13.
/2.
2.1.14.
–4/9. 2.1.15.
{20;4;28}. 2.1.16.
{–19;24;10}. 2.1.17.
25/2;5. 2.1.18.
14;28/
.
2.1.3.
–3. 2.1.4.
26 – 8
.
2.1.5.
– 22. 2.1.6.
–42. 2.1.7.
–1. 2.1.8.
–4. 2.1.9.
–94. 2.1.10.
–262. 2.1.11.
1/2. 2.1.12.
2/7. 2.1.13.
/2.
2.1.14.
–4/9. 2.1.15.
{20;4;28}. 2.1.16.
{–19;24;10}. 2.1.17.
25/2;5. 2.1.18.
14;28/![]() .
2.1.19.
Да. 2.1.20.
Нет. 2.1.21.
Да. 2.1.22.
Нет. 2.1.23.
2;12/25.
2.1.24.
8/3;4/7.
.
2.1.19.
Да. 2.1.20.
Нет. 2.1.21.
Да. 2.1.22.
Нет. 2.1.23.
2;12/25.
2.1.24.
8/3;4/7.
2.2
2.2.1. 2x-3y+4=0. 2.2.2. 3x+y-10=0. 2.2.3. 3x-y-1=0. 2.2.4. x-y+1=0. 2.2.5. x+1=0. 2.2.6. x+y-3=0. 2.2.7. x-y-5=0. 2.2.8. 5x+2y+1=0. 2.2.9. 3x+y+7=0. 2.2.10. 3x+2y+3=0.
2.2.11.
3x-y-3=0. 2.2.12.
arctg
½. 2.2.13.
-/3.
2.2.14.
(-1;4). 2.2.15.
(-8;-2). 2.2.16.
(14;-15). 2.2.17.
(14/3;3). 2.2.18.
x+3y+1=0.
2.2.19.
2x-3y-12=0. 2.2.20.
x+2y+5=0.
2.2.21.
Нет. 2.2.22.
Да. 2.2.23.
Да. 2.2.24.
Нет. 2.2.25.
Да. 2.2.26.
Нет. 2.2.27.
Да. 2.2.28.
Нет. 2.2.29.
Да.
2.2.30.
2/![]() .
2.2.31.
3/2. 2.2.32.
3x-2y+8=0.
2.2.33. x-5y+10=0.
2.2.34.
2x+3y-4=0. 2.2.35.
x-y-4=0. 2.2.36.
3x+2y-5 = 0. 2.2.37.
4x+3y-2 = 0. 2.2.38.
x-
y=0.
.
2.2.31.
3/2. 2.2.32.
3x-2y+8=0.
2.2.33. x-5y+10=0.
2.2.34.
2x+3y-4=0. 2.2.35.
x-y-4=0. 2.2.36.
3x+2y-5 = 0. 2.2.37.
4x+3y-2 = 0. 2.2.38.
x-
y=0.
2.3
2.3.1.
3x-4y-7z=0. 2.3.2.3x+2y+z-7=0.
2.3.3.x-2y-3z=0.
2.3.4.x+y-5=0.
2.3.5.3x+4y-2z-29=0.
2.3.6.
2x-3y+z-11=0. 2.3.7.
x-2y-1=0.
2.3.8.
3x-y+2z-9=0. 2.3.9.
7
/11.
2.3.10.
2![]() /11.
2.3.11.
/3.
2.3.12.
0. 2.3.13.
arccos(1/
/11.
2.3.11.
/3.
2.3.12.
0. 2.3.13.
arccos(1/![]() ).
2.3.14.
Да. 2.3.15.
Нет. 2.3.16.
Да. 2.3.17.
Нет. 2.3.18.
a
= 3, b=
-2/3. 2.3.19.
a = -10/3, b = -6/5. 2.3.20.
19. 2.3.21.
1/7.
2.3.22.
x-2y+z+4=0. 2.3.23.
7x-8y-3z+10=0. 2.3.24.
x-1=0. 2.3.25.
4x+3y+6z-5=0. 2.3.26.
15x-7y-5z=0. 2.3.27.
3x+z-2=0. 2.3.28.
3x+2y-2z+7=0. 2.3.29.
29/
).
2.3.14.
Да. 2.3.15.
Нет. 2.3.16.
Да. 2.3.17.
Нет. 2.3.18.
a
= 3, b=
-2/3. 2.3.19.
a = -10/3, b = -6/5. 2.3.20.
19. 2.3.21.
1/7.
2.3.22.
x-2y+z+4=0. 2.3.23.
7x-8y-3z+10=0. 2.3.24.
x-1=0. 2.3.25.
4x+3y+6z-5=0. 2.3.26.
15x-7y-5z=0. 2.3.27.
3x+z-2=0. 2.3.28.
3x+2y-2z+7=0. 2.3.29.
29/![]() .
2.3.30.
1/
.
2.3.31.
2x-2y+z+15=0,
.
2.3.30.
1/
.
2.3.31.
2x-2y+z+15=0,
h
= 7. 2.3.32.
3x+2y-2z+7=0, h
= 4/![]() .
.
2.4
2.4.1.
![]() =
=
![]() =
;
x = 3t+1, y = 2t+2, z = t. 2.4.2.
=
;
x = 3t+1, y = 2t+2, z = t. 2.4.2.
![]() =
=
![]() =
=
![]() ;
x = -t+1,
;
x = -t+1,
y
= 2t+2, z = 3t-1. 2.4.3.
=
![]() =
=
![]() ;
x = 3t+1, y = 2t+2, z = t. 2.4.4.
;
x = 3t+1, y = 2t+2, z = t. 2.4.4.
![]() =
=
=![]() =
=
![]() ;
x = 2t+3, y = 2t-2, z = t+1. 2.4.5.
=
;
x = 2t+3, y = 2t-2, z = t+1. 2.4.5.
=
![]() =
=
![]() ;
x = 2t+1, y = -5t-3, z = -2t+2. 2.4.6.
;
x = 2t+1, y = -5t-3, z = -2t+2. 2.4.6.
![]() =
=
![]() =
=
![]() ;
x = t-3, y = 2, z = -2t+4. 2.4.7.
=
;
x = t-3, y = 2, z = -2t+4. 2.4.7.
=
![]() =
=
![]() ;
x = t+1, y = 3t-3, z = 2t+2. 2.4.8.
;
x = t+1, y = 3t-3, z = 2t+2. 2.4.8.
![]() =
=
![]() =
;
x = t, y = 3t+1, z = 2t+2. 2.4.9.
=
;
x = t, y = 3t+1, z = 2t+2. 2.4.9.
![]() =
=
![]() =
=
![]() ;
x = -t, y = t, z = t+2. 2.4.10.
;
x = -t, y = t, z = t+2. 2.4.10.
![]() =
=
![]() =
=![]() ;
x = -9t-13/2, y = t-13/6, z = 6t-1. 2.4.11.
;
x = -9t-13/2, y = t-13/6, z = 6t-1. 2.4.11.
![]() =
=
![]() =
;
x = 2t+3, y = -3t-2, z = t+1. 2.4.12.
=
=
;
x = 2t+3, y = -3t-2, z = t+1. 2.4.12.
=
![]() =
=
![]() ;
x = t+1, y = 2t-3, z = -t+2. 2.4.13.
Да. 2.4.14.
Нет. 2.4.15.
Да. 2.4.16.
Нет.
2.4.17.
;
x = t+1, y = 2t-3, z = -t+2. 2.4.13.
Да. 2.4.14.
Нет. 2.4.15.
Да. 2.4.16.
Нет.
2.4.17.
(-1;3;5).
2.4.18.
(2;3;-4). 2.4.19.
![]() =
=
=
=
![]() ;
x = -3t-1, y = 2t+2, z = 2t+1. 2.4.20.
;
x = -3t-1, y = 2t+2, z = 2t+1. 2.4.20.
![]() =
=
![]() =
=
![]() ;
x = t+2, y = t-2, z = -t+3. 2.4.21.
Да. 2.4.22.
Да. 2.4.23.
Да. 2.4.24.
Да. 2.4.25.
Да. 2.4.26.
Да.
;
x = t+2, y = t-2, z = -t+3. 2.4.21.
Да. 2.4.22.
Да. 2.4.23.
Да. 2.4.24.
Да. 2.4.25.
Да. 2.4.26.
Да.
Раздел III.
3.1
3.1.1.
1140. 3.1.2.
![]() . 3.1.3.
166167000. 3.1.4.
210. 3.1.5.
840. 3.1.6.
10. 3.1.7.
15. 3.1.8.
84. 3.1.9.
а)
7140; б)
595; в)
4; г)
84; д)
816.
. 3.1.3.
166167000. 3.1.4.
210. 3.1.5.
840. 3.1.6.
10. 3.1.7.
15. 3.1.8.
84. 3.1.9.
а)
7140; б)
595; в)
4; г)
84; д)
816.
3.1.10. 504 числа; 648 чисел. 3.1.11. 1320 способов; 110 способов.
3.1.12.
1680; 336. 3.1.13.
2520. а)
360; б)
60. 3.1.14.
80. 3.1.15.
а)
![]() ;
б)
;
б)
![]() .
.
3.1.16. 720; 120. 3.1.17. 120. а) 24; б) 48. 3.1.18. 60. а) 12; б) 24.
3.1.19.
![]() .
а)
120; б)
.
а)
120; б)
![]() .
3.1.20.
A52
= 20. 3.1.21.
85=32768.
.
3.1.20.
A52
= 20. 3.1.21.
85=32768.
3.2
3.2.1.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3.2.2.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
.
,
.
3.2.3.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.![]() ,
,
![]() ,
,
![]() ,
,
![]() 3.2.5.
0,7. 3.2.6.
0,75. 3.2.7.
0,06. 3.2.8.
3.2.5.
0,7. 3.2.6.
0,75. 3.2.7.
0,06. 3.2.8.
![]() 3.2.9.
3.2.9.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() . 3.2.10.
a)
. 3.2.10.
a)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() ,
,
![]() . 3.2.11.
а)
0,6; б)
1)
. 3.2.11.
а)
0,6; б)
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() . 3.2.12.
. 3.2.12.
![]() ,
,
![]() ,
,
![]() . 3.2.13.
. 3.2.13.
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3.2.14.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() .
.
3.2.15.
![]() . 3.2.16.
а)
. 3.2.16.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() . 3.2.17.
а)
. 3.2.17.
а)
![]() ;
б)
;
б)
![]() .
.
3.2.18.
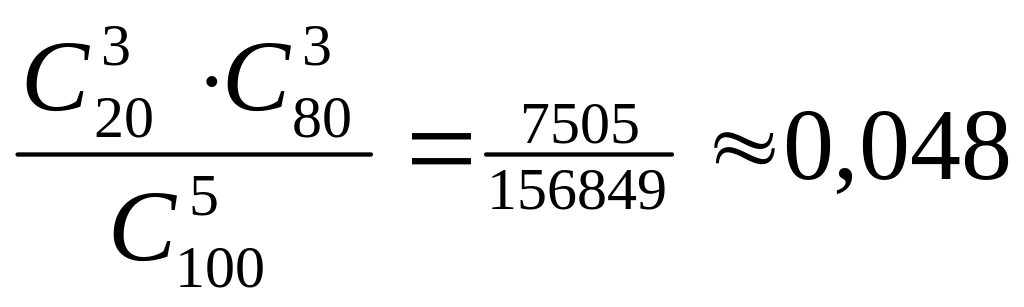 . 3.2.19.
а)
. 3.2.19.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
3.2.20.
а)
;
б)
![]() ;
в)
;
в)
![]() . 3.2.21.
. 3.2.21.
![]() . 3.2.22.
. 3.2.23.
. 3.2.22.
. 3.2.23.
![]() .
.
3.2.24.
а)
![]() =
=
![]() ;
б) 1-
;
б) 1-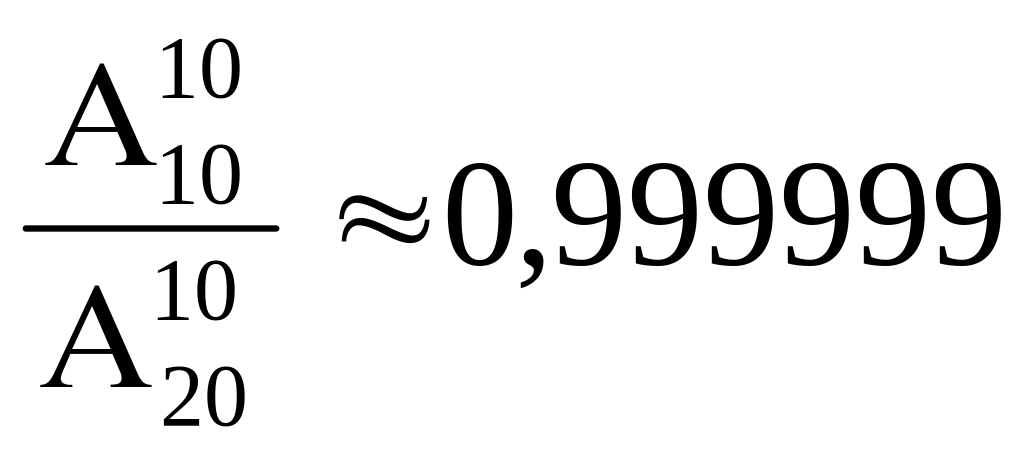 ;
в)
;
в)
 =
=
![]() ;
;
г)
 ;
д)
;
д)
![]() . 3.2.25.
. 3.2.25.
![]() ;
;
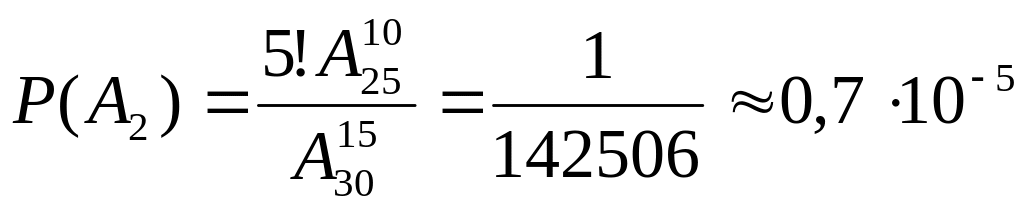 ;
;
![]() ;
;
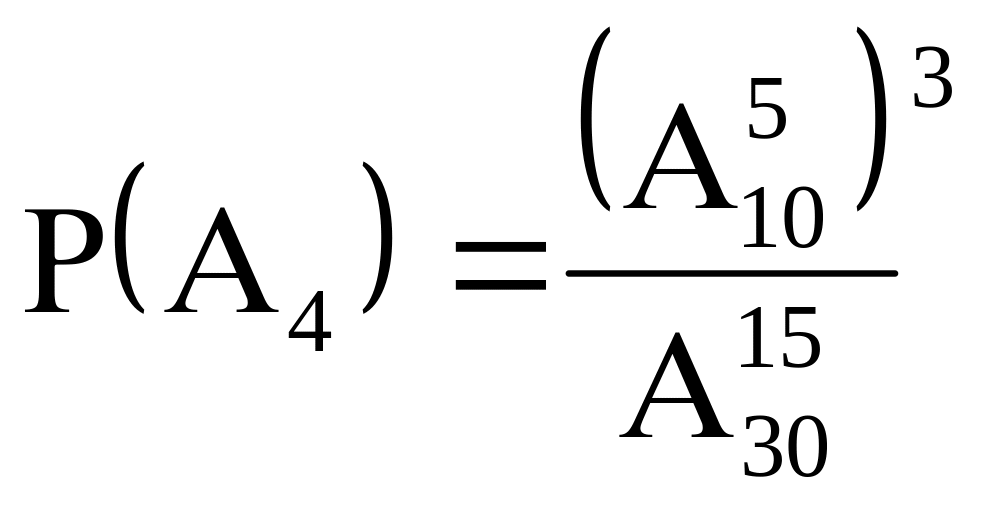 .
.
3.2.26.
![]() . 3.2.27.
.
3.2.28.
P(A)
= 1/6, P(B)
= 5/12, P(C)
= 1/2, P(D)
= 35/36. 3.2.29.
P(A)
= 7!/77.
3.2.30.
P(A)
= 24/125 =0,192, P(B)
= 101/125=0,808.
. 3.2.27.
.
3.2.28.
P(A)
= 1/6, P(B)
= 5/12, P(C)
= 1/2, P(D)
= 35/36. 3.2.29.
P(A)
= 7!/77.
3.2.30.
P(A)
= 24/125 =0,192, P(B)
= 101/125=0,808.
3.2.31.
P(A)=24/625.
3.2.32.
P(A)
= 12/25 = 0,48. 3.2.33.
P(A)
= 7/40, P(B)
= 1/120, P(C)
= 17/24. 3.2.34.
P(A)
= 0,181. 3.2.35.
P(A)
= 25/646
![]() 0,0387. 3.2.36.
P(A)
= 16/25.
0,0387. 3.2.36.
P(A)
= 16/25.
3.3.
3.3.1.
Попарно несовместны события: А1
и А4,
А3
и А4.
![]() -
выпавшее число четно;
-
выпавшее число четно;
![]() -
выпала единица или двойка; А1А2
– выпало число 3; А1+А2
– выпало нечетное число или число 6;
А1А3=А1,
А1+А3=А3,
А1А4=
Ø,
А1+А4
– выпало число, меньшее 4, или число 6;
А1А5
– выпало число 3; А2А3
– выпало число 3 или 5; А2А5
– выпало число 3; А2+А5
– выпало число, не равное 6; А3А4
= Ø;
А3+А4=
;
А3А5
– выпало число 3 или 4; А3+А5
– выпало число, не равное 1; А4+А5
– выпало число, не больше 4; А1+А2+А5
=
.
-
выпала единица или двойка; А1А2
– выпало число 3; А1+А2
– выпало нечетное число или число 6;
А1А3=А1,
А1+А3=А3,
А1А4=
Ø,
А1+А4
– выпало число, меньшее 4, или число 6;
А1А5
– выпало число 3; А2А3
– выпало число 3 или 5; А2А5
– выпало число 3; А2+А5
– выпало число, не равное 6; А3А4
= Ø;
А3+А4=
;
А3А5
– выпало число 3 или 4; А3+А5
– выпало число, не равное 1; А4+А5
– выпало число, не больше 4; А1+А2+А5
=
.
3.3.2.
Попарно несовместные события: А1
и А4,
А2 и
А4.
![]() - бракованных калькуляторов – 4 или 5;
-
число бракованных калькуляторов не
равно трем;
- бракованных калькуляторов – 4 или 5;
-
число бракованных калькуляторов не
равно трем;
![]() -
бракованных калькуляторов - не более
трех;
-
бракованных калькуляторов - не более
трех;
![]() -
все пять калькуляторов – без брака;
А1А3
– бракованных калькуляторов оказалось
2 или 3; А1+А3=
;
А2А3=А2;
А2+А3=А3;
А1А5
– число бракованных калькуляторов от
1 до 3; А1+А5=
;
А2+А4
– есть хотя бы три бракованных
калькулятора; А2А5=А2;
А3А4=А4;
А3+А4=А3.
-
все пять калькуляторов – без брака;
А1А3
– бракованных калькуляторов оказалось
2 или 3; А1+А3=
;
А2А3=А2;
А2+А3=А3;
А1А5
– число бракованных калькуляторов от
1 до 3; А1+А5=
;
А2+А4
– есть хотя бы три бракованных
калькулятора; А2А5=А2;
А3А4=А4;
А3+А4=А3.
3.3.3.
События А1,
А2,
А3,
А4 попарно
несовместны. Кроме того, несовместны
пары событий А1
и А6,
А3
и А7,
А4
и А7.
-
обнаружены не все дефекты или дефектов
не обнаружено вообще;
-
дефекты не обнаружены;
![]() -
обнаружено три или четыре дефекта;
А1А5=А1;
А1+А5=А5;
А1А6=
Ø; А1+А6
– обнаружен хотя бы один дефект (событие
А5);
А1А7=А1;
А1+А7=А7;
А3А4=
Ø; А3+А4
– обнаружено три или четыре дефекта;
А5А7
- обнаружен один или два дефекта; А5+А7=
;
А6А7
– обнаружено два дефекта (событие А2);
А6+А7=
;
А2+А3+А4
– обнаружено хотя бы два дефекта (событие
А6).
-
обнаружено три или четыре дефекта;
А1А5=А1;
А1+А5=А5;
А1А6=
Ø; А1+А6
– обнаружен хотя бы один дефект (событие
А5);
А1А7=А1;
А1+А7=А7;
А3А4=
Ø; А3+А4
– обнаружено три или четыре дефекта;
А5А7
- обнаружен один или два дефекта; А5+А7=
;
А6А7
– обнаружено два дефекта (событие А2);
А6+А7=
;
А2+А3+А4
– обнаружено хотя бы два дефекта (событие
А6).
3.3.4.
А1+А2А3+А4. 3.3.5.
(А1+А2)![]() (А4+А5). 3.3.6.
0,2.
(А4+А5). 3.3.6.
0,2.
3.3.7.
![]() . 3.3.8.
. 3.3.8.
![]() . 3.3.9.
. 3.3.9.
![]() и
и
![]() . 3.3.10.
. 3.3.10.
![]() и
.
и
.
3.3.11.
![]() . 3.3.12.
. 3.3.12.
![]() и
и
![]() 3.3.13.
0,72.
3.3.14.
0,98. 3.3.15.
0,999. 3.3.16.
0,99999. 3.3.17.
3.3.13.
0,72.
3.3.14.
0,98. 3.3.15.
0,999. 3.3.16.
0,99999. 3.3.17.
![]() 3.3.18.
0,992.
3.3.19.
0,86. 3.3.20.
0,52. 3.3.21.
а)
3.3.18.
0,992.
3.3.19.
0,86. 3.3.20.
0,52. 3.3.21.
а)
![]() ;
б)
;
б)
![]() 3.3.22.
а)
3.3.22.
а)
![]() б)
б)![]() в)
в)
![]() г)
г)
![]() 3.3.23. а)
3.3.23. а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)
![]() 3.3.24.
0,24.
3.3.25.
0,21.
3.3.24.
0,24.
3.3.25.
0,21.
3.3.26. P(A) = 8/57. 3.3.27. P(A) = 1/72. 3.3.28. P(A) = 0,18. 3.3.29. P(A) = 0,944;
P(B) = 0,392; P(C) = 0,468; P(D) = 0,144, P(E)=0,856. 3.3.30. P(A) = 23/75.
3.4.
3.4.1.
0,032. 3.4.2.
0,9. 3.4.3.
0,015. 3.4.4.
0,122. 3.4.5.
![]() 3.4.6.
3.4.6.
![]()
3.4.7.
![]() 3.4.8.
0,4. 3.4.9.
3.4.8.
0,4. 3.4.9.
![]() 3.4.10.
3.4.10.
![]() 3.4.11.
3.4.11.
![]() 3.4.12.
0,75.
3.4.13.
3.4.12.
0,75.
3.4.13.
![]() 3.4.14.
3.4.14.![]() 3.4.15.
В
первой. 3.4.16.
а)
3.4.15.
В
первой. 3.4.16.
а)
![]() б)
б)
![]()
в)
![]() 3.4.17.
а)
3.4.17.
а)
![]() б)
б)
![]() 3.4.18.
Гипотеза
Н1. 3.4.19.
P(A)
= 0,122. 3.4.20.
P(A)
= 64/105. 3.4.21.
P(A)
= 0,47. 3.4.22.
P(A)
= 5/11. 3.4.23.
P(A)
= 27/28.
3.4.18.
Гипотеза
Н1. 3.4.19.
P(A)
= 0,122. 3.4.20.
P(A)
= 64/105. 3.4.21.
P(A)
= 0,47. 3.4.22.
P(A)
= 5/11. 3.4.23.
P(A)
= 27/28.
3.5.
3.5.1.
а)
![]() б)
б)![]() в)
в)
![]() 3.5.2.
а)
0,3087; б)
3.5.2.
а)
0,3087; б)
![]() в)
в)![]() 3.5.3.
а)
0,1536;
3.5.3.
а)
0,1536;
б)
0,5904; в) 0,9984; г) 0,0256. 3.5.4.
а)
0,0729; б)
![]() 3.5.5.
а)
3.5.5.
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)![]() д)
д)
![]() е)
е)![]() 3.5.6.
а)
3.5.6.
а)
![]()
б)
![]() 3.5.7.
Три
телевизора. 3.5.8.
3.5.7.
Три
телевизора. 3.5.8.![]() 3.5.9.
а)
3.5.9.
а)
![]()
б)
![]() 3.5.10.
а)
3.5.10.
а)
![]() б)
б)
![]() 3.5.11.
а)
3.5.11.
а)
![]() б) 0,5768.
б) 0,5768.
3.5.12.
а)
![]() б)
б)
![]() 3.5.13.
а)
3.5.13.
а)
![]() б)
б)
![]() 3.5.14.а)
3.5.14.а)![]() ;
б)
в)
;
б)
в)
![]() г)
г)
![]() 3.5.15.
а)
3.5.15.
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() 3.5.16.
а)
3.5.16.
а)
![]() б)
б)
![]() в)
в)
![]() 3.5.17.
а)
3.5.17.
а)
![]()
б)
![]() в) 0,0228. 3.5.18.
а)
0,0072; б) 0,9993. 3.5.19.
а)
0,0582; б) 0,9968. 3.5.20.
а)
в) 0,0228. 3.5.18.
а)
0,0072; б) 0,9993. 3.5.19.
а)
0,0582; б) 0,9968. 3.5.20.
а)
![]() б)
б)
![]() в)
в)
![]() 3.5.21.
а)
0,0797; б) 0,516. 3.5.22.
3.5.21.
а)
0,0797; б) 0,516. 3.5.22.
![]() 3.5.23.
3.5.23.
![]() 3.5.24.
P(A)<P(B). 3.5.25.
P(A)
= 8/81. 3.5.26.
P(A)
= 0,328;
3.5.24.
P(A)<P(B). 3.5.25.
P(A)
= 8/81. 3.5.26.
P(A)
= 0,328;
P(B) = 0,41, P(C)=0,08. 3.5.27. P(A) = 10/243; P(B) = 211/243. 3.5.28. n= 7. 3.5.29. P(A) = 1-5/e2 ˜ 0,31. 3.5.30. P(A) = 0,9973. 3.5.31. (1) Ф(10)+Ф(1,25)? 0,5+0,3944= 0,8944; (2) Ф(3,75)+Ф(40) = 0,4999+0,5=0,9999; (3) Ф(2)+Ф(2)= 0,9545. 3.5.32. 2Ф(2,0004) = 0,9545.
3.6.
3.6.1. а) 0,5; б) 0,7; в) 0,8; г) 0,2; д) 0,8;

е) 0, если х -1;
F(x)= 0,2, если –1<x 0; M[X]=0,4; D[X]=1,24.
0,7, если 0<x 2;
1, если x>2.
3.6.2. а) 0,7; б) 0,5; в) 0,7; г) 0,5;

д) 0, если х 1,
0,2, если 1<x 2,
F(x)= 0,3, если 2<x 3, е) M[X]= 3,1; ж) D[X]=2,09.
0,7, если 3<x![]()
1, если x>5.
3.6.3.р1=![]() р2=
р2=![]() а)
а)
![]() б)
б)
![]() в)
г)
в)
г)
![]() 3.6.4. р1=
3.6.4. р1=![]() р2=
р2=![]() а)
б)
1; в)
г)
а)
б)
1; в)
г)
![]()
3.6.5. а)
xi |
0 |
1 |
1,5 |
3 |
pi |
3/5 |
1/5 |
2/15 |
1/15 |
б)
0,6; в) 0,74; г)
д)
![]()
3.6.6. а)
xi |
-2 |
0 |
1 |
2 |
рi |
1/3 |
1/2 |
1/12 |
1/12 |
![]()
3.6.7.
хi |
0 |
1 |
2 |
pi |
2/21 |
10/21 |
3/7 |
M[X]=![]() D[X]=
D[X]=![]()
3.6.8.
xi |
-50 |
50 |
250 |
450 |
pi |
0,94 |
0,03 |
0,02 |
0,01 |
M[X]=-36.
3.6.9.
xi |
0 |
1 |
2 |
pi |
0,06 |
0,38 |
0,56 |
M[X]=1,5; D[X]=0,37.
3.6.10.
а)
xi |
0 |
1 |
2 |
3 |
4 |
pi |
1/16 |
1/4 |
3/8 |
1/4 |
1/16 |
б) M[X]=2, D[X]=1.
3.6.11.
a)
xi |
0 |
1 |
2 |
3 |
pi |
0,512 |
0,384 |
0,096 |
0,008 |
б) M[X]=0,6; D[X]=0,48.
3.6.12.
M[X]=0,15;
D[X]=0,1425;
![]() 3.6.13. M[X]=2;
D[X]=1,2;
3.6.13. M[X]=2;
D[X]=1,2;
![]() 3.6.14. 3
и 2,7. 3.6.15. а)
60; б) 300 тыс. долларов. 3.6.16.
3.6.14. 3
и 2,7. 3.6.15. а)
60; б) 300 тыс. долларов. 3.6.16.
![]() 3.6.17.
3.6.17.
![]() Надо класть
5 изюминок на булку. 3.6.18.
Две опечатки
с вероятностью, равной
Надо класть
5 изюминок на булку. 3.6.18.
Две опечатки
с вероятностью, равной
![]() 3.6.19. Три
элемента. 3.6.20.
P(A)=16/(4!e2)
= 0,09. 3.6.21.
P(A)
= 0,6; P(B)
= 0,1. 3.6.22.
P(A)
= 1-1/e5
= 0,994. 3.6.23.
M(X) = 0. 3.6.24.
M(X) = 3. 3.6.25.
M(X) = 3/5. 3.6.26.
M(X) = 1/p.
3.6.19. Три
элемента. 3.6.20.
P(A)=16/(4!e2)
= 0,09. 3.6.21.
P(A)
= 0,6; P(B)
= 0,1. 3.6.22.
P(A)
= 1-1/e5
= 0,994. 3.6.23.
M(X) = 0. 3.6.24.
M(X) = 3. 3.6.25.
M(X) = 3/5. 3.6.26.
M(X) = 1/p.
3.7.
3.7.1.
а)
1,5; б) 0,5; в) 0; г) 0,6; д)
![]() 3.7.2.
а)
0,5; б) 0,75; в)
3.7.2.
а)
0,5; б) 0,75; в)![]() г)
г)
![]() 3.7.3.
а) 2500; б)
3.7.3.
а) 2500; б)![]() в)
в)
![]() г)
г)
![]() д)
д)![]() 3.7.4.
а)
2е2;
б)
3.7.4.
а)
2е2;
б)
![]() в)
в)
![]() 3.7.5.
1).
а) 0,25; б)
3.7.5.
1).
а) 0,25; б)![]() в)
в)
![]() 2). а)
2). а)
![]() б)
б)
![]() в)
в)
![]() 3.7.6.
а)
3.7.6.
а)![]() б) 15; в) 75.
3.7.7. а)
б) 15; в) 75.
3.7.7. а)![]() б)
б)
![]() 3.7.8.
M[X]=
3.7.8.
M[X]=![]() D[X]=
D[X]=![]()
3.7.9.
![]() 3.7.10. Ф(2)+Ф(1)
0,8185.
3.7.11.
3.7.10. Ф(2)+Ф(1)
0,8185.
3.7.11.
![]() 3.7.12.
1)
M[X]=2,
D[X]=9,
3.7.12.
1)
M[X]=2,
D[X]=9,
![]() ;
2) M[X]=3,
D[X]=25,
;
2) M[X]=3,
D[X]=25,
![]() 3.7.13.
3.7.13.
![]() Точность
изготовления – 0,329. 3.7.14.
3.7.15.
Точность
изготовления – 0,329. 3.7.14.
3.7.15.
![]() 3.7.16.
3.7.17.
3.7.16.
3.7.17.![]() 3.7.18.
3.7.18.
![]() 3.7.19. а)
(-5;25); б) (0;20); в) (6,625; 13,375). 3.7.20.
(4,85;
5,15). 3.7.21.
M[X]=15,39;
=3,26.
3.7.22.
3.7.19. а)
(-5;25); б) (0;20); в) (6,625; 13,375). 3.7.20.
(4,85;
5,15). 3.7.21.
M[X]=15,39;
=3,26.
3.7.22.
![]() 3.7.23.
3.7.23.
![]() 3.7.24.
f(x)
= 1/((1+x2));
P(0<X<1)=1/4;
нет. 3.7.25.
P(-100<X<100)=Ф(1,3)+Ф(2)=
0,88. 3.7.26.
P(1<X<2) = 0,12. 3.7.27.
M(X)
=
(b+a)/2; D(X) = (b-a)2/12.
3.7.28.
M(X)=1, D(X)=1/3. 3.7.29.
Ф(15)+Ф(3)= 0,5+0,4986=0,9986. 3.7.30.
Ф(3)+Ф(1) = 0,4986+0,3413 = 0,8399.
3.7.24.
f(x)
= 1/((1+x2));
P(0<X<1)=1/4;
нет. 3.7.25.
P(-100<X<100)=Ф(1,3)+Ф(2)=
0,88. 3.7.26.
P(1<X<2) = 0,12. 3.7.27.
M(X)
=
(b+a)/2; D(X) = (b-a)2/12.
3.7.28.
M(X)=1, D(X)=1/3. 3.7.29.
Ф(15)+Ф(3)= 0,5+0,4986=0,9986. 3.7.30.
Ф(3)+Ф(1) = 0,4986+0,3413 = 0,8399.
3.8.
3.8.1. а) 0,05; 0,45; 0,6; 0,9;
б)
xi |
-1 |
1 |
P(X=xi) |
0,2 |
0,8 |
в) зависимы;
г)
yj |
0 |
1 |
2 |
P(Y=yj) |
0,4375 |
0,3125 |
0,25 |
M[Y/X=1]=0,8125;
д)
(mX,
mY)=(0,6;
0,8), DX=0,64,
DY=0,66,
KXY=0,02,
![]()
3.8.2.
p=0,15;
P(X=0, Y=0)=0,15; P(X
Y)=0,82;
P![]()
б)
xi |
-1 |
0 |
1 |
|
yj |
0 |
1 |
P(X=xi) |
0,42 |
0,2 |
0,38 |
P(Y=yj) |
0,2 |
0,8 |
в) зависимы; г) M[Y/X=1]=0,079;
yj |
0 |
1 |
P(Y=yj / X=1) |
0,921 |
0,079 |
д)
(mX,mY)=(-0,04;
0,8), DX=0,7984,
DY=0,16,
KXY=-0,058,
![]()
3.8.3.
![]()
xi |
0 |
1 |
2 |
б) |
xi |
0 |
1 |
2 |
P(X=xi) |
¼ |
½ |
¼ |
|||||
0 |
1/4 |
0 |
0 |
|
||||
1 |
1/3 |
1/6 |
0 |
yj |
0 |
1 |
2 |
|
2 |
1/9 |
1/9 |
1/36 |
P(Y=yj) |
25/36 |
5/18 |
1/36 |
|
в) зависимы;
г)
yj |
0 |
1 |
2 |
P(Y=yj/X=1) |
2/3 |
1/3 |
0 |
M[Y/X=1]=![]() д)
(mX,
mY)=(1,
),
DX=
д)
(mX,
mY)=(1,
),
DX=![]() DY=
DY=![]() KXY=
KXY=![]()
![]()
3.8.4.
xi |
0 |
1 |
|
xi |
0 |
1 |
P(X=xi) |
½ |
½ |
||||
0 |
1/3 |
1/6 |
|
|||
1 |
1/3 |
1/6 |
yj |
0 |
1 |
|
|
P(Y=yj) |
2/3 |
1/3 |
|||
Независимы.
mX=
mY=![]() DX=
DX=![]() DY=
DY=![]()
3.8.5.
xi |
0 |
1 |
|
xi |
0 |
1 |
2 |
P(X=xi) |
0,36 |
0,48 |
0,16 |
||||
0 |
0 |
0,36 |
|
||||
1 |
0,24 |
0,24 |
yj |
0 |
1 |
|
|
2 |
0,16 |
0 |
P(Y=yj) |
0,4 |
0,6 |
||
mX=0,8,
mY=0,6,
DX=0,48,
DY=0,24,
![]() Зависимы.
Зависимы.
3.8.6.
-
 yj
yjxi
0
1
3.8.7. а)
yj
xi
0
1
0
0,08
0,32
0
2/3
2/9
1
0,12
0,48
1
1/12
1/36
![]() Независимы.
Независимы.
б)
-
yj
xi
0
1
0
5/9
1/3
1
0
1/9
![]() Зависимы
Зависимы
3.8.8.
xi |
0 |
1 |
3 |
P(X=xi) |
0 |
0,05 |
0,1 |
0,15 |
0,3 |
1 |
0,2 |
0,2 |
0,3 |
0,7 |
P(Y=yj) |
0,25 |
0,3 |
0,45 |
|
mX=0,7, mY=1,65, KXY= - 0,055. Зависимы.
СПИСОК ЛИТЕРАТУРЫ
1. Сборник задач по математике для втузов. Ч.3. Теория вероятностей и математическая статистика / Под ред. А.В. Ефимова. М.: Наука, 1990.
2. Ганнушкина С.А. Сборник задач по теории вероятностей. М.: РГГУ.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математиче-ской статистике. М.: Высшая школа, 1975.
4. Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, 1980.
5. Цаленко М.Ш., Лавриненко Т.А. Дискретная математика. Теоретический курс и сборник задач. М.: РГГУ,1995.

 yj
yj
 yj
yj yj
yj yj
yj