
- •Российский экономический университет им. Г.В. Плеханова
- •Часть II
- •Российский экономический университет
- •Часть II
- •Содержание
- •Раздел I. Линейная алгебра.
- •Раздел II. Аналитическая геометрия.
- •Раздел III. Теория вероятностей.
- •Раздел 1. Линейная алгебра.
- •Система линейных уравнений. Метод Гаусса.
- •Арифметическое векторное пространство.
- •1.3. Матрицы.
- •Определители.
- •Раздел II. Аналитическая геометрия.
- •2.1. Скалярное и векторное произведения векторов.
- •2.2. Прямая на плоскости.
- •2.3. Плоскость.
- •2.4. Прямая в пространстве.
- •Раздел III. Теория вероятностей.
- •3.1. Элементы комбинаторики: сочетания, размещения, перестановки.
- •3.2. Понятие случайного события. Классическое определение вероятности события.
- •3.3. Операции над событиями. Условная вероятность. Теоремы сложения и умножения вероятностей.
- •3.4. Формула полной вероятности. Формула Бейеса.
- •3.5. Формула Бернулли. Теорема Пуассона. Локальная и интегральная теоремы Лапласа.
- •3.6. Закон распределения, функция распределения и числовые характеристики дискретной случайной величины (дсв). Законы распределения: биноминальный, Пуассона.
- •3.7. Плотность распределения, функция распределения и числовые характеристики непрерывной случайной величины (нвс). Нормальное распределение.
- •3.8. Законы распределения и числовые характеристики случайных векторов.
- •Раздел I.
- •Раздел II.
- •Раздел III.
Российский экономический университет им. Г.В. Плеханова
М.В. Зайцев, Т.А. Лавриненко, А.А. Туганбаев
Высшая математика
Сборник задач
Часть II
Москва 2013
Российский экономический университет
им. Г.В. Плеханова
Одобрено УМС факультета
Протокол №_________
«____»______2013 года
Председатель______
М.В. Зайцев, Т.А. Лавриненко, А.А. Туганбаев
Высшая математика
Сборник задач
Часть II
Рекомендовано
Кафедрой ВМ
Протокол № 10
«___»______2013 года
Зав. кафедрой_______
Москва 2013
Содержание
Раздел I. Линейная алгебра.
Система линейных уравнений. Метод Гаусса.
Арифметическое векторное пространство.
Матрицы.
Определители.
Раздел II. Аналитическая геометрия.
2.1. Скалярное и векторное произведение векторов.
2.2. Прямая на плоскости.
2.3. Плоскость.
2.4. Прямая в пространстве.
Раздел III. Теория вероятностей.
3.1. Элементы комбинаторики: сочетания, размещения, перестановки.
3.2. Понятие случайного события. Классическое определение вероятности события.
3.3. Операции над событиями. Условная вероятность. Теоремы сложения и умножения вероятностей.
3.4. Формула полной вероятности. Формула Бейеса.
3.5. Формула Бернулли. Теорема Пуассона. Локальная и интегральная теоремы Лапласа.
3.6. Закон распределения, функция распределения и числовые характеристики дискретной случайной величины (ДСВ). Законы распределения: биноминальный, Пуассона.
3.7. Плотность распределения, функция распределения и числовые характеристики непрерывной случайной величины (НСВ). Нормальное распределение.
3.8. Законы распределения и числовые характеристики случайных векторов.
Раздел 1. Линейная алгебра.
Система линейных уравнений. Метод Гаусса.
1.1.1. Решить систему методом Гаусса:
а)
 б)
б)

в)
 г)
г)

д)
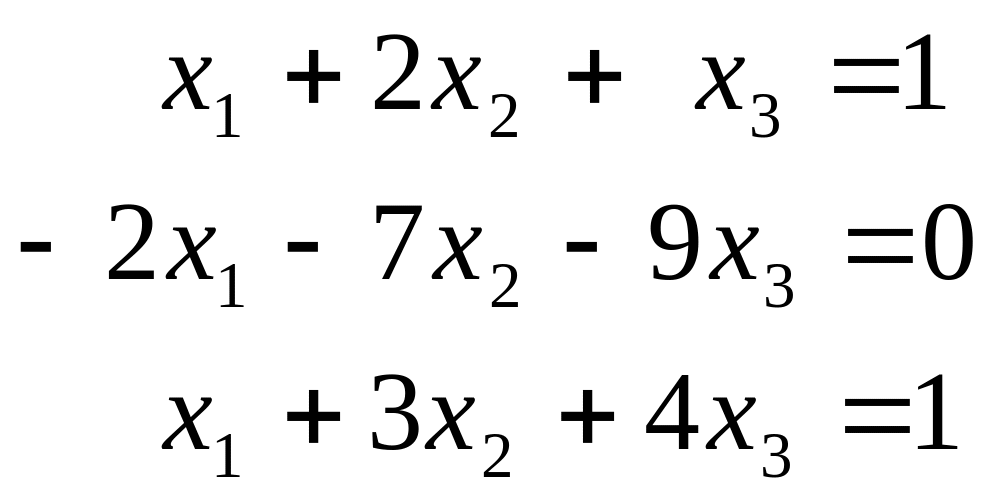 е)
е)
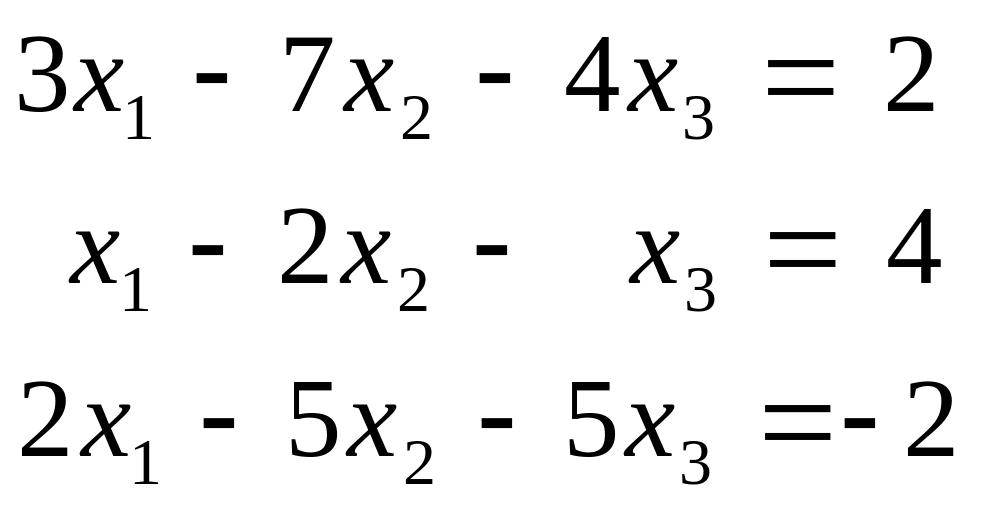
1.1.2. Решить систему методом Гаусса:
а)
 б)
б)

в)
 г)
г)
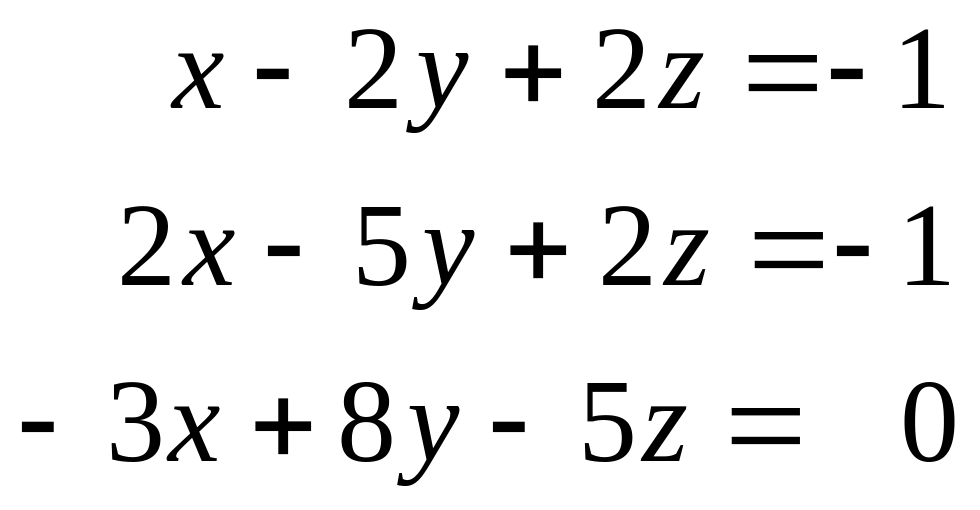
Исследовать на совместность и найти общее решение системы уравнений:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
Исследовать на совместность и найти общее решение системы:
а)
 б)
б)
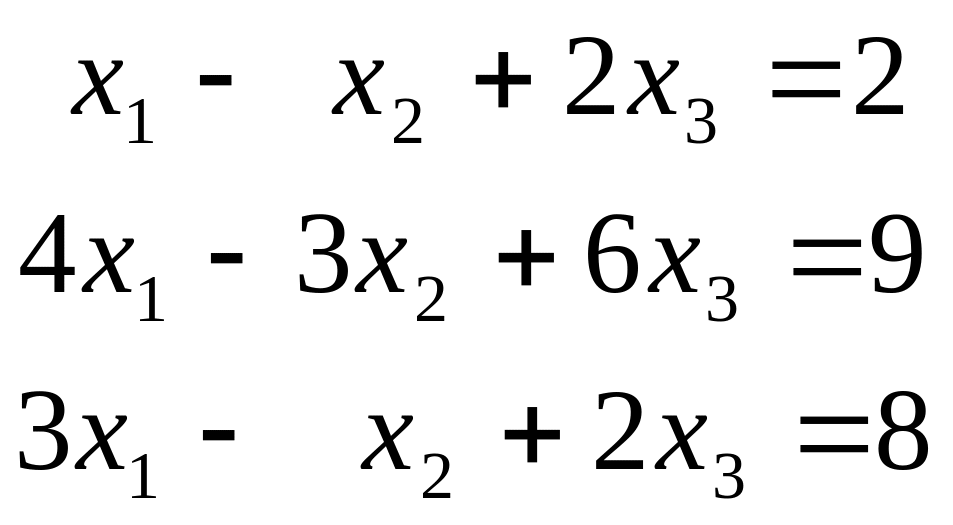
в)
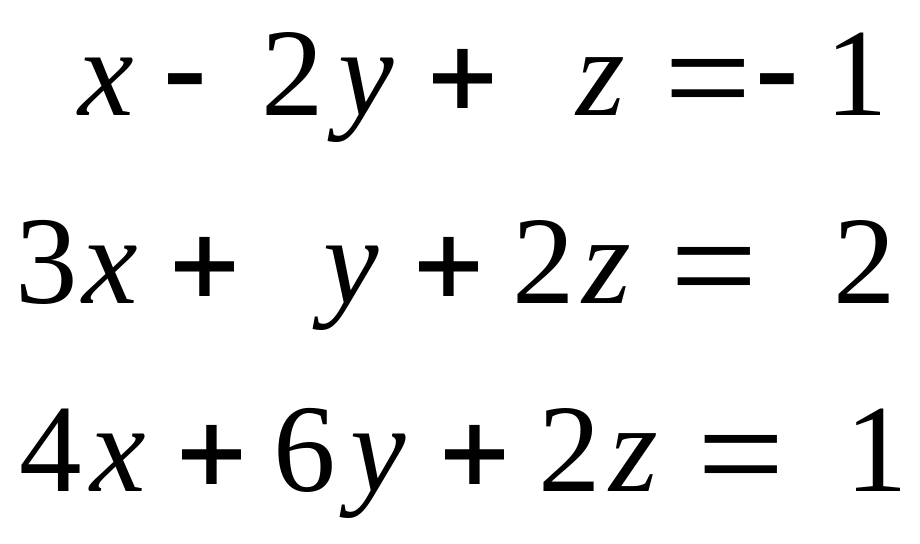 г)
г)
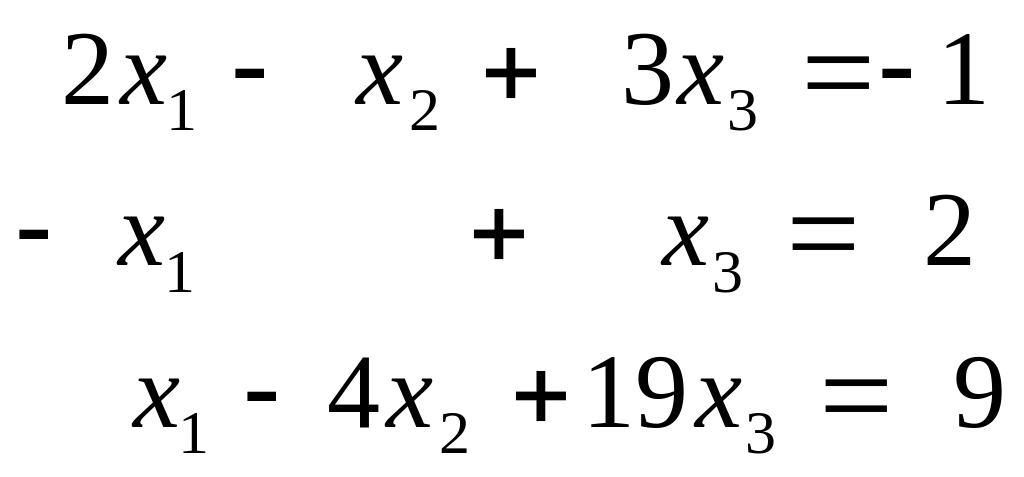
Исследовать на совместность, найти общее и одно частное решение системы:
а)
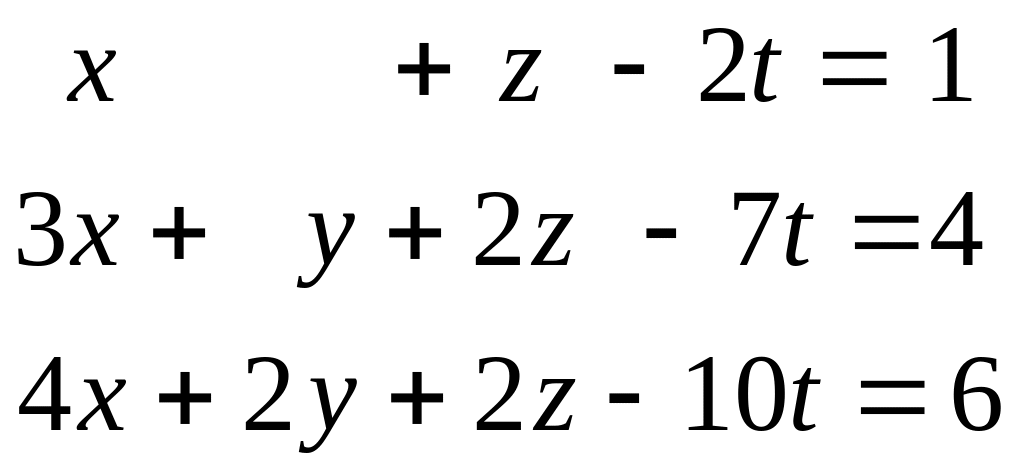 б)
б)

в)
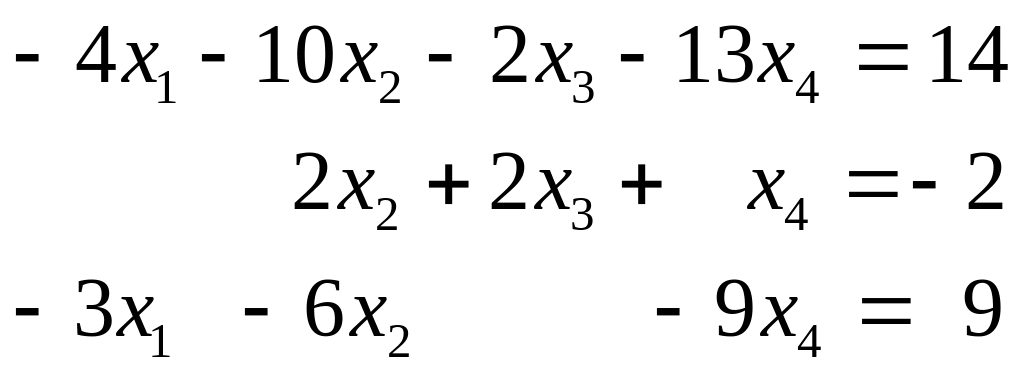 г)
г)

д)
 е)
е)

Найти общее решение системы:
а )
 б)
б)

в )
 г)
г)
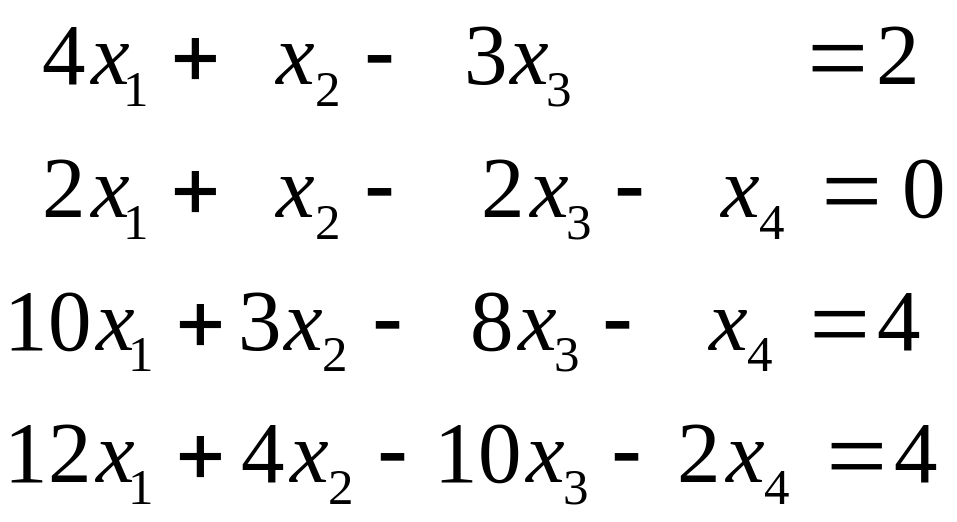
д)
 е)
е)
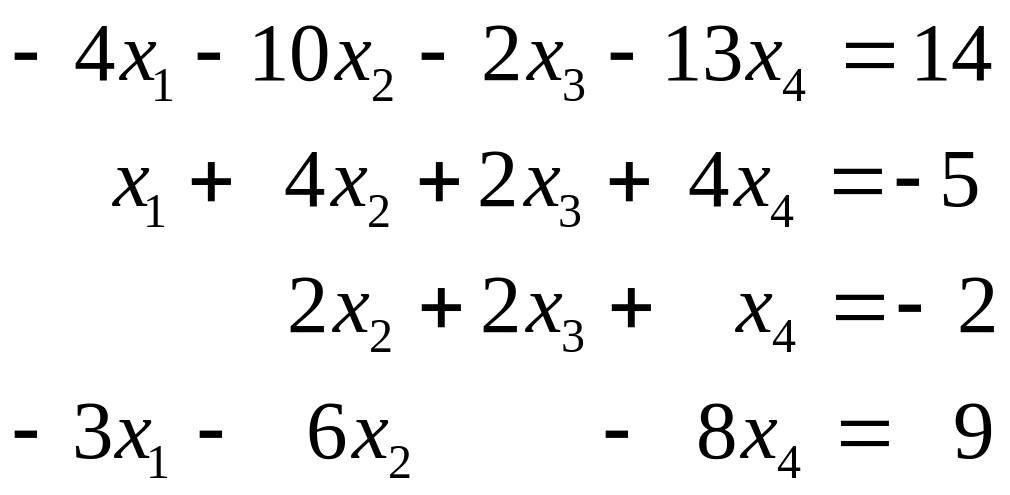
ж)
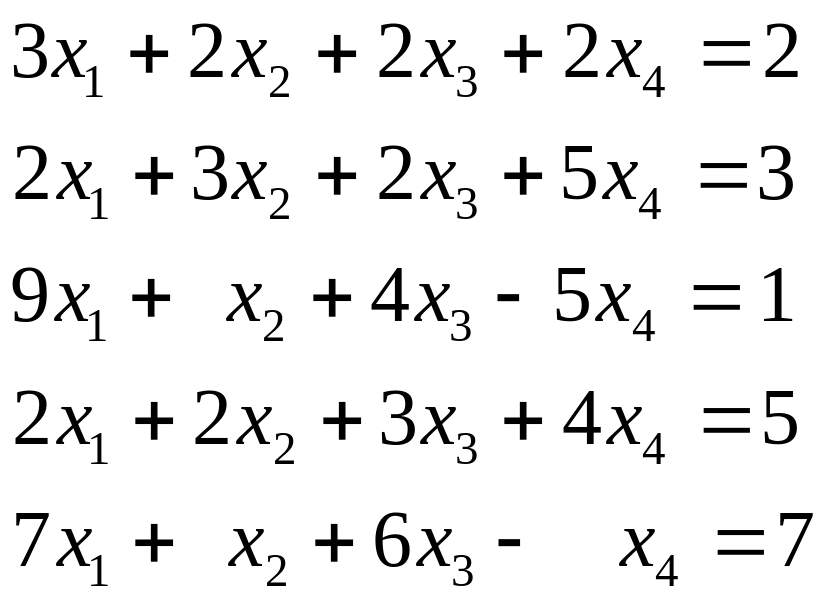 з)
з)

и)
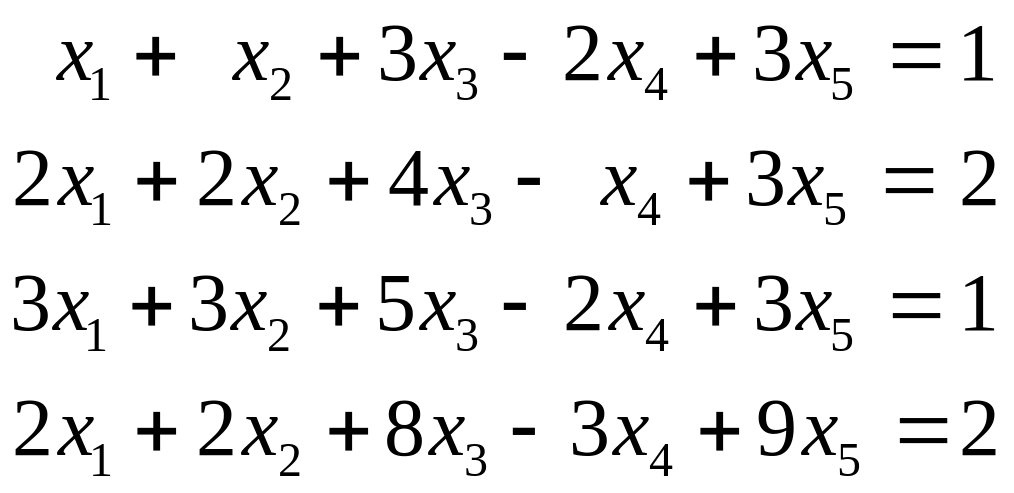 к)
к)
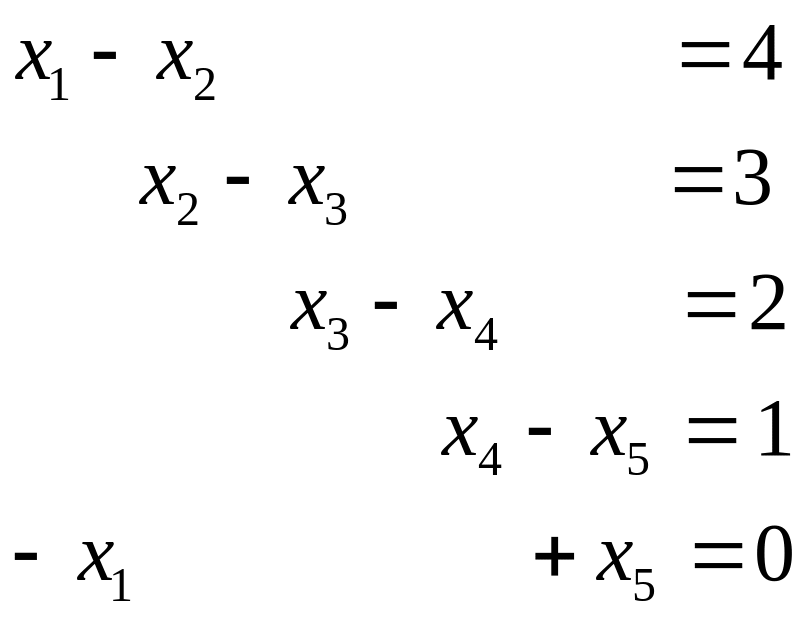
Найти фундаментальную систему решений однородной системы уравнений:
а)
![]() б)
б)
![]()
в)
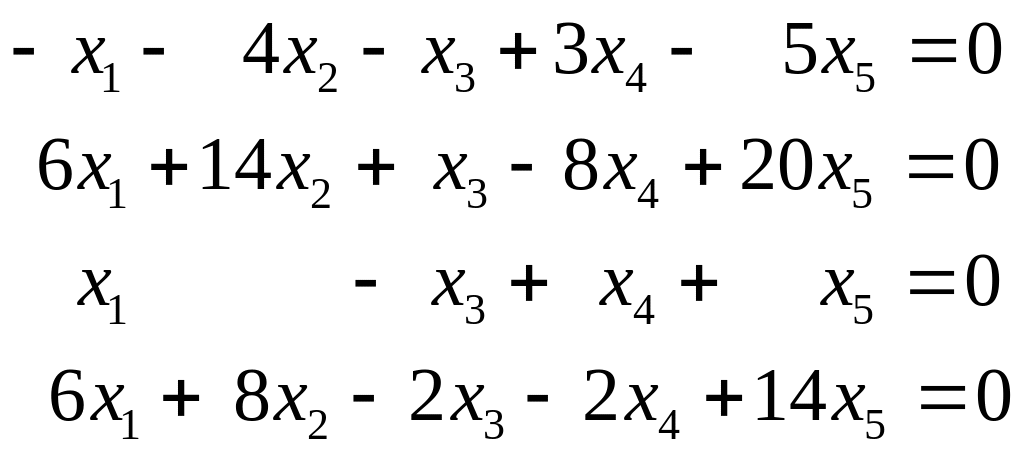 г)
г)

Методом Гаусса решить систему уравнений, заданную матрицей А и столбцом свободных членов В:
а)
![]() б)
б)

в)
 г)
г)

