Комбинации машин Тьюринга: разветвление
Пусть
имеются три машины Тьюринга:
.
Заданное
слово обрабатывается
,
которая выдает некоторое заключительное
слово и останавливается. Также имеется
некоторое условие, если оно выполняется,
то заключительное слово
передается в качестве начального слова
в
,
иначе оно передается в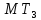
.
Любая из этих машин обрабатывает ленту
до попадания в своё стоп-состояние.
Программу
можно построить следующим образом:
Пусть
имеет два стоп-состояния:
,
каждое из которых отождествляется с
начальными состояниями
и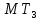
соответственно. Стоп-состояния
и
со стоп-состоянием
Начальное состояние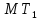
– начальное состояние
Полученная
таким образом машина называется
разветвлением
на
и
.
Комбинации машин Тьюринга: разветвление с циклом.
Пусть у нас
есть разветвление
на
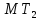и
.
Добавим условие: по окончанию работы
её результат передается в
.
В данном
случае
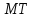будем называть разветвлением
на
и
с циклом.
Вычислимые по Тьюрингу функции.
Будем
говорить, что Машина Тьюринга правильно
вычисляет частичную числовую функцию
,
если для любого набора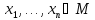
имеет место следующее:
Если
определена на
,
то Машина, стандартно воспринимая
данный набор в состоянии
,
остановится через конечное число шагов
и будет стандартно воспринимать
в состоянии
Если
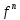не определена на
,
то Машина, стандартно воспринимая набор
в состоянии
будет работать бесконечно.При своей работе Машина никогда не заходит в левую зону.
Разрешимые (рекурсивные) множества. Пример. Рекурсивно перечислимые множества. Пример.
Пусть
.
Пусть
Будем говорить чтоM–
разрешимо(рекурсивно), если существуют
две такие Машины ТьюрингаPиQ, что:
Если таких машин не существует, то М – неразрешимо.
Пример:
Множество
.
означает что МТ остановится на х через
какое-то чисто шагов.
Множество рекурсивно перечислимо, если существует машина Тьюринга Р такая, что
,
но не существует Машины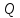
такой, что
.
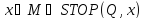Пример: Н
– множество таких номеров х Машин
,
которые останавливаются на своем
собственном номере х.
Алгоритмически неразрешимые проблемы. Пример. Тезис Тьюринга.
Алгоритмически неразрешимая проблема– проблема, для которой не существует алгоритма решения.
Пример:
Существует ли Машина Тьюринга, которая для произвольной машины Тьюринга определяла бы самоприменима данная машина или нет?
Тезис Тьюринга:
Всякий алгоритм может быть реализован подходящей машиной Тьюринга.