- •Оглавление
- •Высказывания. Примеры высказываний. Пропозициональные переменные. Определения основных логических операций.
- •Теорема о подстановке ппф вместо пропозициональной переменной в тождественно истинной формуле.
- •Теорема о существовании эквивалентной днф
- •Теорема о существовании эквивалентной кнф
- •Теоремы о виде тождественно ложной днф, тождественно истинной кнф
- •Понятия сднф, скнф. Построение сднф, скнф по таблице истинности данной формулы.
- •Построение сднф по данной днф.
- •Построение скнф по данной кнф
- •Условия существования скнф, сднф
- •Понятие логического следствия в ав. Содержательный пример.
- •Непротиворечивые (выполнимые) и противоречивые (невыполнимые) множества посылок. Примеры.
- •Установление факта логического следствия из данного множества посылок по таблице истинности.
- •Установление факта логического следствия из данного множества посылок путем определения совместности соответствующей системы логических уравнений.
- •Понятие алгебраической системы данной сигнатуры
- •Характерные черты алгоритма
- •Элементы модели алгоритма
- •Основные предположения об элементах модели алгоритма
- •Устройство машины Тьюринга
- •Комбинации машин Тьюринга: композиция
- •Комбинации машин Тьюринга: разветвление
- •Комбинации машин Тьюринга: разветвление с циклом.
- •Вычислимые по Тьюрингу функции.
- •Разрешимые (рекурсивные) множества. Пример. Рекурсивно перечислимые множества. Пример.
- •Алгоритмически неразрешимые проблемы. Пример. Тезис Тьюринга.
Непротиворечивые (выполнимые) и противоречивые (невыполнимые) множества посылок. Примеры.
Множество посылок называется выполнимым, если существует такой набор пп, что они все одновременно принимают значениеt.
Пример:
Если завтра мало пар и не к первой, то я пойду в универ.
A– мало пар (если мало, тоt)
B– не к первой паре (если не к первой, тоt)
C– я пойду в универ (если пойду, тоt)
Формулировка

|
A |
B |
C |
|
|
F |
F |
F |
T |
|
F |
F |
T |
T |
|
F |
T |
F |
T |
|
F |
T |
T |
T |
|
T |
F |
F |
T |
|
T |
F |
T |
T |
|
T |
T |
F |
F |
|
T |
T |
t |
T |
A,B, множество посылок является выполнимым.
множество посылок является выполнимым.
Множество посылок называется невыполнимым, если такого набора не существует.
Пример:
Если завтра мало пар, не к первой, а я – девушка, то я пойду в универ.
«Я девушка» - тождественно ложное высказывание, значит множество посылок невыполнимо.
Установление факта логического следствия из данного множества посылок по таблице истинности.
Составляем таблицу истинности
Ищем строки, в которых все посылки =t
Если заключение в каждой из этих строк =t, то это логическое следствие.
Если завтра мало пар и не к первой, то я пойду в универ.
A– мало пар (если мало, тоt)
B– не к первой паре (если не к первой, тоt)
C– я пойду в универ (если пойду, тоt)
Формулировка

A,B, множество посылок, С – заключение
множество посылок, С – заключение
|
A |
B |
C |
|
|
F |
F |
F |
T |
|
F |
F |
T |
T |
|
F |
T |
F |
T |
|
F |
T |
T |
T |
|
T |
F |
F |
T |
|
T |
F |
T |
T |
|
T |
T |
F |
F |
|
T |
T |
T |
T |
Значит это логическое следствие.
Установление факта логического следствия из данного множества посылок путем определения совместности соответствующей системы логических уравнений.
Пусть
 – множество посылок,
– множество посылок, – заключение.
– заключение.
Проверяем
 на выполнимость, если
на выполнимость, если – невыполнимо, то
– невыполнимо, то ,
если нет, то переходим к пункту 2
,
если нет, то переходим к пункту 2Составляем систему вида:

Если система несовместна, то
 ,
иначе – нет.
,
иначе – нет.
Основные теоремы о логическом следствии (сведение установления факта логического следствия из данного множества посылок к установлению факта логического следствия из другого множества посылок)
Пусть
 – какое-то множество посылок,
– какое-то множество посылок, – ппф.
– ппф.

Если
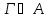 ,
то
,
то
Если
 ,
то
,
то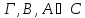
Если
 и
и ,
то
,
то
Если
 ,
то
,
то
Основные теоремы о логическом следствии (сведение установления факта логического следствия из данного множества посылок к проверке тождественной истинности или тождественной ложности формул АВ)
 если
если
 если:
если: если
если
 если
если тождественно ложна.
тождественно ложна.
Схемы аксиом ИВ. Получение аксиом из схем аксиом ИВ. Пример.
В качестве схем аксиом ИВпримем следующие выражения:
В схемах
аксиом
 - любые ппф.Аксиомы исчисления
высказыванийполучаются из приведенных
схем при подстановке в них ппф.
- любые ппф.Аксиомы исчисления
высказыванийполучаются из приведенных
схем при подстановке в них ппф.
Пример:
 получается при подстановке в А1 при
получается при подстановке в А1 при
Правило выводаmodusponens. Пример применения

 – любые ппф.
– любые ппф. называется непосредственным следствием
формул
называется непосредственным следствием
формул
Пример:
Из А10
 при
при получим
получим
Из А1
 при
при получим
получим
Применим
MPс

Таким
образом, мы вывели формулу (доказали
теорему)
 .
.
Понятие доказательства в ИВ. Понятие исчисления.
Формула
 доказуема (выводима) в ИВ если существует
конечная последовательность формул
доказуема (выводима) в ИВ если существует
конечная последовательность формул ,
обладающая следующими свойствами:
,
обладающая следующими свойствами:
 - аксиома
- аксиома
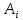 выводится при помощиmodusponensиз ранее выведенных
формул.
выводится при помощиmodusponensиз ранее выведенных
формул.
Исчислением
 называется множество всех формул,
доказуемых из аксиом множества
называется множество всех формул,
доказуемых из аксиом множества при помощи правил вывода
при помощи правил вывода
Понятие доказательства из гипотез в ИВ
Формула
 доказуема (выводима) из множества гипотез
доказуема (выводима) из множества гипотез если существует конечная последовательность
формул
если существует конечная последовательность
формул обладающая следующими свойствами:
обладающая следующими свойствами:
 – аксиома или
– аксиома или

 выводится с помощью правила выводаmodusponensиз
ранее выведенных формул
выводится с помощью правила выводаmodusponensиз
ранее выведенных формул
Основные теоремы о доказуемости из гипотез в ИВ.

Если
 ,
то
,
то
Если
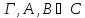 ,
то
,
то
Если
 и
и ,
то
,
то
Если
 и
и ,
то
,
то
Если
 ,
то
,
то
Теорема о дедукции в ИВ
Если
 ,
то
,
то
Понятие производного допустимого правила вывода в ИВ. Пример.
Все допустимые правила вывода, отличные от MP, будем называтьпроизводными допустимыми правилами вывода.
Пример:
 – введение конъюнкции.
– введение конъюнкции.
Технология доказательства с использованием произвольных допустимых правил вывода: сведение к подзадачам. Пример.
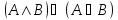

Теорема о совпадении множества тождественно истинных формул АВ и доказуемых формул ИВ: план доказательства
Для доказуемости формулы в ИВ необходимо и достаточно, чтобы она была тождественно истинной формулой АВ.
Пусть у нас
есть
 .
Для проверки факта доказуемости
рассмотрим
.
Для проверки факта доказуемости
рассмотрим
 .
Формула не является тождественно
истинной, значит не доказуема.
.
Формула не является тождественно
истинной, значит не доказуема.
Связь между наличием факта логического следствия в АВ и тождественной истинностью вложенной импликации посылок и логического следствия этих посылок
 тогда и только тогда, когда
тогда и только тогда, когда
Связь между наличием факта логического следствия в АВ и доказуемостью из гипотез в ИВ.
 тогда и только тогда, когда
тогда и только тогда, когда
Непротиворечивость ИВ
Исчисление
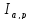 называетсяпротиворечивым, если
существует такая формула
называетсяпротиворечивым, если
существует такая формула ,
что
,
что и
и .
Если такой формулы не существует, то
исчисление назовемнепротиворечивым.
.
Если такой формулы не существует, то
исчисление назовемнепротиворечивым.
Понятие алгебраической системы
Алгебраической
системой
 назовем множествоMс
заданными на нем некоторыми функциями
назовем множествоMс
заданными на нем некоторыми функциями и некоторыми предикатами
и некоторыми предикатами
Такую
систему будем обозначать

Если предикатов нет, то система называется алгеброй.
Если функций нет, то система называется моделью.4
Алфавит и язык АП. Сигнатура. Понятие терма данной сигнатуры. Пример. Ппф АП. Пример. Предложение. Пример.
Алфавит

 – множество предметных переменных.
– множество предметных переменных.
 – множество предикатных символов
– множество предикатных символов
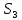 – множество функциональных символов
– множество функциональных символов
 – множество предметных констант
– множество предметных констант
 – множество логических символов
– множество логических символов
 – вспомогательные символы (запятая,
скобочки)
– вспомогательные символы (запятая,
скобочки)
 – сигнатура
– сигнатура
Языком
алгебры предикатовсигнатуры назовем множество всех слов в алфавите
назовем множество всех слов в алфавите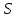 .
.
Понятие термаопределим как:
Предметная переменная есть терм
Предметная константа есть терм
 – терм
– термНикаких других термов нет
Пример:
 – терм
– терм
 – не терм
– не терм
Понятие
ппф сигнатуры
 определим следующим образом:
определим следующим образом:
Атомная ппф сигнатуры
 есть ппф сигнатуры
есть ппф сигнатуры
 – пп,
– пп, – ппф сигнатуры
– ппф сигнатуры
 – ппф
– ппф – ппф
– ппф – ппф
– ппф – ппф
– ппф – ппф
– ппф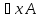 – ппф
– ппф
Никаких других ппф нет.
Пример:
 –
ппф
–
ппф
Формула, не содержащая свободных переменных, называется предложением.
Пример:
 -
предложение
-
предложение