14. Теорема о существовании эквивалентной днф

Для любой ппф АВ существует эквивалентная ей днф.

15. Теорема о существовании эквивалентной кнф

Для любой ппф алгебры высказываний существует эквивалентная ей кнф.

16. Теоремы о виде тождественно ложной днф, тождественно истинной кнф

Если –тождественно ложная днф, то любая её элементарная конъюнкция содержит некоторую пропозициональную переменную вместе с тесным отрицанием этой же пропозициональной переменной.

Если –тождественно истинная кнф, то любая элементарная дизъюнкция содержит некоторую пропозициональную переменную вместе с тесным отрицанием этой пропозициональной переменной.

17. Понятия сднф, скнф. Построение сднф, скнф по таблице истинности данной формулы.

Совершенная дизъюнктивная нормальная форма (сднф)– днф, в которой каждая её элементарная конъюнкция зависит от всех входящих в неё пп и каждая пп входит в каждую элементарную конъюнкция ровно один раз.

Совершенная конъюнктивная нормальная форма (скнф)– кнф, в которой каждая её элементарная дизъюнкция зависит от всех входящих в неё пп и каждая пп входит в каждую элементарную дизъюнкцию ровно один раз.

Построение сднф по таблице истинности данной формулы:

1. Находим строки, где итоговая формула принимает значение t.

2. Для каждой такой строки создаем элементарную конъюнкцию по правилу: если пп=t, то просто добавляем, если пп=f, то добавляем со знаком.

3. Из полученных элементарных конъюнкций составляем днф.

4. Получаем что-то типа .

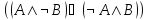Построение скнф по таблице истинности данной формулы:

1. Находим строки, где итоговая формула принимает значение f.

2. Для каждой такой строки создаем элементарную дизъюнкцию по правилу: если пп=f, то просто добавляем, если пп=t, то добавляем со знаком.

3. Из полученных элементарных дизъюнкций составляем кнф.

4. Получаем что-то типа

18. Построение сднф по данной днф.

1. Убеждаемся что данная нам днф не является тождественно ложной

2. В каждую элементарную конъюнкцию дописываем недостающие пп как

3. Совершаем необходимые преобразования, пока не придем к сднф.

19. Построение скнф по данной кнф

1. Убеждаемся что данная нам кнф не является тождественно истинной

2. В каждую элементарную дизъюнкцию дописываем недостающие пп как

3. Совершаем необходимые преобразования, пока не придем к скнф.

20. Условия существования скнф, сднф

Для тождественно ложной ппф не существует эквивалентной сднф.

Для тождественно истинной ппф не существует эквивалентной скнф.

21. Понятие логического следствия в ав. Содержательный пример.

Высказывание называется логическим следствием высказыванийв АВ, если ппфпринимает значениеtкаждый раз, когда все формулыпринимают значениеt.

Факт логического следствия будем записывать как

Замечание 1:

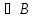означает чтотождественно истинна.

Замечание 2:

не является логическим следствиемесли, а.

Замечание 3:

Если – невыполнимы, топри любом.

Множество посылок называется выполнимым, если существует такой набор пп, что они все одновременно принимают значение t.

Содержательный пример:

1. Если завтра мало пар и не к первой, то я пойду в универ.

A– мало пар (если мало, тоt)

B– не к первой паре (если не к первой, тоt)

C– я пойду в универ (если пойду, тоt)

Формулировка

A,B,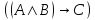множество посылок, С – заключение

A	B	C
F	F	F	T
F	F	T	T
F	T	F	T
F	T	T	T
T	F	F	T
T	F	T	T
T	T	F	F
T	T	t	T

Значит это логическое следствие.

2. Если завтра мало пар, не к первой, а я – девушка, то я пойду в универ.

«Я девушка» - тождественно ложное высказывание, значит множество посылок невыполнимо, значит это логическое следствие по замечанию 3.