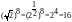1.2.Действия со степенями

Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь. М. В. Ломоносов

Это интересно. Оказывается, древние греки умели возводить в квадрат и в куб. Названия для второй и третьей степени числа древнегреческого происхождения: «дюнамис» — квадрат, «кюбос» — куб.

Древний Вавилон. Вавилоняне пошли дальше: составили и пользовались таблицами квадратов и кубов чисел, которыми мы пользуемся в настоящее время.

Это интересно. Широко используют степень астрономы, которым на каждом шагу приходится встречаться с огромными числами и еще производить с ними вычисления. Например, масса Солнца — .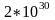

Степени также используют в биологии, химии, без них не было бы вычислительной техники.

Древние славяне тоже умели записывать большие числа, для этого у них были специальные названия: «тысяча», «тьма», «легион», «леодр».

Вопросы:

1. Какое выражение называют степенью?

2. Приведите примеры степеней с различными основаниями.

3. Какие действия со степенями можно выполнять? Опишите правила действий со степенями.

1 .2.1. Терминология

Степень

– основание степени

– показатель степени

1.2.2.Определения степеней с различными показателями

1.Степень с натуральным показателем (n N)

2.Степень с отрицательным показателем (n N)

3.Степень с рациональным показателем (n,m N)

4. Степень с нулевым показателем

а0=1

1.2.3.Правила действий со степенями

формулы	примеры
Умножение степеней с одинаковыми основаниями аn*am= an+m Чтобы перемножить степени с одинаковыми основаниями, надо основание степени оставить тем же, а показатели степеней сложить.	25*2-3 = 25+(-3) = 22=4 a3,5*a-0,5 = a3,5-0,5 = a3
Деление степеней с одинаковыми основаниями аn:am= an-m Чтобы разделить степени с одинаковыми основаниями, надо основание степени оставить тем же, а показатели степеней вычесть.	53:52 = 53-2 =5 х6:х-2=х6-(-2)=х8
3.Возведение степени в степень (an)m = anm Чтобы возвести степень в степень, надо показатели степеней перемножить.	(76)1/2 = 73
4. Возведение произведения в степень (ab)n = an*bn Чтобы возвести произведение в степень, достаточно возвести в степень каждый множитель.	(16*3)2 =162*32 =28*32 (аb-2)5=а5*(b-2)5=а5*b-10=
5.Возведение дроби в степень Чтобы возвести дробь в степень, достаточно возвести в степень числитель и знаменатель.