
- •43.02.11 Гостиничный сервис
- •Часть 1.
- •Часть 2
- •Часть 3
- •Тема 1: Повторение школьного курса
- •Структура множества действительных чисел.
- •4. Множество целых чисел.
- •5. Множество рациональных чисел.
- •1.1.2.Арифметические действия в r.
- •5. Деление
- •1 .1.3.Проценты
- •Нахождение % от числа, например,
- •Нахождение числа по данному проценту, например,
- •Нахождение процентного отношения одного числа от другого.
- •При решении многих задач удобно пользоваться формулой сложных процентов:
- •1.1.4.Индивидуальные задания-из-1
- •1.1.5. Из материалов егэ Найдите значение выражений
- •1.2.Действия со степенями
- •1 .2.1. Терминология
- •1.2.2.Определения степеней с различными показателями
- •1.2.3.Правила действий со степенями
- •1.2.4.Примеры:
- •15) Исправьте ошибку
- •1.2.5. Индивидуальные задания-из-2
- •Из материалов егэ
- •1.3.Тождественные преобразования алгебраических выражений
- •3А*(2,5а3), (5аb2)*(0,4c3d), x2y*(-2z)*0,75 – одночлены!!!
- •1.3.1.Основные тождественные преобразования
- •1.3.2.Формулы сокращенного умножения
- •1.3.3.Из материалов егэ
- •1.3.4.Индивидуальные задания – из-3
- •1.4.Линейные уравнения и неравенства
- •1.4.1. Линейные уравнения
- •Самостоятельно:
- •1.4.2. Задачи, решаемые с помощью уравнений
- •1.4.3. Линейные неравенства
- •1.4.4. Индивидуальные задания
- •1.4.5.Из материалов егэ
- •1.5. Метод интервалов
- •1.5.1.Алгоритм:
- •1.5.2.Примеры:
- •1.5.3. Индивидуальные задания
- •1.6. Квадратные уравнения и неравенства
- •Где х1 и х2 – корни уравнения
- •1.6.1.Примеры
- •1.6.2. Из материалов егэ
- •1.6.3. Индивидуальные задания
- •1.7.Системы уравнений и неравенств
- •1.7.1. Системы уравнений
- •1.7.2. Системы неравенств
- •1.7.3.Индивидуальные задания
- •1.8.Функции: свойства, графики
- •1.8.1.Линейная функция
- •1.8.2 .Квадратичная функция
- •Справка
- •1.8.4.Индивидуальные задания
- •1.9. Графическое решение уравнений и систем уравнений
- •1.9.1.Графический способ решения уравнений
- •Графическое решение системы уравнений
- •1.10. Демонстрационный вариант контрольной работы №1: Повторение школьного курса
- •Приложения Ответы
- •Глоссарий
1.9. Графическое решение уравнений и систем уравнений
1.9.1.Графический способ решения уравнений
Для того, чтобы решить уравнение графическим способом (графически), необходимо выполнить следующие действия:
Построить график левой части уравнения
у1 = Левая часть
Построить график правой части уравнения
у2 = Правая часть
Если графики пересеклись, то:
количество корней равно количеству точек пересечения
абсциссы (х) точек пересечения являются корнями уравнения
Если графики не пересеклись, то уравнение корней не имеет.
Для справки:
Графики часто встречающихся функций – см.пункт 1.8.3.Справка.
Замечания:
График функции у = f(x)+ C получается из графика функции у = f(x) параллельным переносом по оси ординат (у) вверх, если С > 0 и вниз, если С<0.
График функции у = f(x+С) получается из графика функции у = f(x) параллельным переносом по оси абсцисс (х) влево, если С > 0 и вправо, если С<0.
График функции у = │f(x)│ ) получается из графика функции у = f(x) отображением части графика, расположенной ниже оси абсцисс, на верхнюю полуплоскость.
График функции у = f(│x│)получается из графика функции у = f(x) отображением части графика, расположенной справа от оси ординат, симметрично оси на левую полуплоскость.
Иногда, прежде, чем строить график, уравнение удобно преобразовать. Например: уравнение х3+4=х2+3х удобно записать в виде: х3 =х2+3х-4.
Пример:
Сколько корней имеет уравнение х2-3х-10=│х│? Назовите приближенные значения корней.
Решение
Пусть у1= х2-3х-10 – парабола
Ветви направлены вверх, т.к. а=1>0
Точки пересечения параболы с осями:
С осью х: х2-3х-10=0, х1=5,х2=-2
С осью у: х=0, у(0)=-10.
Координаты вершины параболы:
х0=1,5, у0=у(1,5)= -
Следовательно, вершина парабола в точке А(1,5;…)
Пусть у2=│х│ - «галочка»
Получаем

Ответ: уравнение имеет 2 корня.
Решите уравнения графически:
х2-9=2х+7
х2-6х+7=х3-2
4-х2=х+1
Решите уравнения графически - самостоятельно!
-
Вариант
Задание
Вариант
Задание
1
х2-5х-14=х3
6
√х=-2х+3
2
х2+2х+15=-2х+6
7
х=х3+2
3
х2-1=3х+9
8
6х-х2=9-х
4
│х│=х2+2х-8
9
х2-4х= - │х│
5
х3-1=х2-2х
10
х2+2х=-2х-9
Графическое решение системы уравнений
Для того, чтобы решить систему уравнений графическим способом, нужно выполнить следующие действия:
Построить график первого уравнения, выразив из него «у1»
Построить график второго уравнения, выразив из него «у2»
Найти координаты точек пересечения графиков у1 и у2, если они пересеклись. Количество точек пересечения равно количеству решений системы.
Если графики не пересеклись, то это означает, что система решений не имеет.
Пример:
Сколько решений имеет система уравнений?

Решение
Из первого уравнения:
 -
гипербола. Вычислим несколько конкретных
точек:
-
гипербола. Вычислим несколько конкретных
точек:х
1
2
-1
-2
У
2
1
-2
-1
Из второго уравнения: у2=5-х2 – парабола:
а) Ветви направлены вниз, т.к. а=-1< 0
б) Точки пересечения параболы с осями:
С осью х: 5-х2=0,
х1=+ ,х2=-
,х2=-
С осью у: х=0, у(0)=5.
в) Координаты вершины параболы:
х0=0, у0=5
Следовательно, вершина парабола в точке А(0;5)
*. Как можно было иначе построить параболу?
Получаем:

Очевидно, что система имеет 3 решения, т.к. графики пересеклись в 3 точках.
Ответ: система имеет 3 решения.
Решите системы графически:
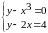 2.
2.
 3.
3.
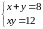 4.
4.
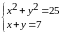 5.
5.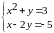
Ответы: 1) (2;8); 2) (1;-2) и (-1,5;-3,25) 3) (2;6) и (6;2) 4) (3;4) и (4;3) 5)(-1;2) и (0,5;2,75)
Решите систему самостоятельно:
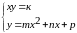 (k,m,n,p
возьмите из таблицы)
(k,m,n,p
возьмите из таблицы)
-
вариант
данные
к
1
4
6
1
4
6
1
1
m
-0.5
-2
0.5
1
2
-0.5
-1
1
n
0
12
1
4
12
1
2
2
p
2
-14
-4.5
2
14
4.5
1
-1
