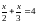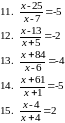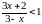- •43.02.11 Гостиничный сервис
- •Часть 1.
- •Часть 2
- •Часть 3
- •Тема 1: Повторение школьного курса
- •Структура множества действительных чисел.
- •4. Множество целых чисел.
- •5. Множество рациональных чисел.
- •1.1.2.Арифметические действия в r.
- •5. Деление
- •1 .1.3.Проценты
- •Нахождение % от числа, например,
- •Нахождение числа по данному проценту, например,
- •Нахождение процентного отношения одного числа от другого.
- •При решении многих задач удобно пользоваться формулой сложных процентов:
- •1.1.4.Индивидуальные задания-из-1
- •1.1.5. Из материалов егэ Найдите значение выражений
- •1.2.Действия со степенями
- •1 .2.1. Терминология
- •1.2.2.Определения степеней с различными показателями
- •1.2.3.Правила действий со степенями
- •1.2.4.Примеры:
- •15) Исправьте ошибку
- •1.2.5. Индивидуальные задания-из-2
- •Из материалов егэ
- •1.3.Тождественные преобразования алгебраических выражений
- •3А*(2,5а3), (5аb2)*(0,4c3d), x2y*(-2z)*0,75 – одночлены!!!
- •1.3.1.Основные тождественные преобразования
- •1.3.2.Формулы сокращенного умножения
- •1.3.3.Из материалов егэ
- •1.3.4.Индивидуальные задания – из-3
- •1.4.Линейные уравнения и неравенства
- •1.4.1. Линейные уравнения
- •Самостоятельно:
- •1.4.2. Задачи, решаемые с помощью уравнений
- •1.4.3. Линейные неравенства
- •1.4.4. Индивидуальные задания
- •1.4.5.Из материалов егэ
- •1.5. Метод интервалов
- •1.5.1.Алгоритм:
- •1.5.2.Примеры:
- •1.5.3. Индивидуальные задания
- •1.6. Квадратные уравнения и неравенства
- •Где х1 и х2 – корни уравнения
- •1.6.1.Примеры
- •1.6.2. Из материалов егэ
- •1.6.3. Индивидуальные задания
- •1.7.Системы уравнений и неравенств
- •1.7.1. Системы уравнений
- •1.7.2. Системы неравенств
- •1.7.3.Индивидуальные задания
- •1.8.Функции: свойства, графики
- •1.8.1.Линейная функция
- •1.8.2 .Квадратичная функция
- •Справка
- •1.8.4.Индивидуальные задания
- •1.9. Графическое решение уравнений и систем уравнений
- •1.9.1.Графический способ решения уравнений
- •Графическое решение системы уравнений
- •1.10. Демонстрационный вариант контрольной работы №1: Повторение школьного курса
- •Приложения Ответы
- •Глоссарий
1.4.5.Из материалов егэ
Решите уравнения:
1.4-2х=-4х+5
2.5х-2(7+5х)=-4х-10 3. 4. 5. 6. 7. 8.
|
|
Решите задачи:
1.Коэффициент
полезного действия (КПД) некоторого
двигателя определяется формулой
 ,
где Т1
– температура нагревателя (в градусах
Кельвина), Т2
– температура холодильника. При какой
минимальной температуре нагревателя
Т1
КПД двигателя будет не меньше 45%, если
температура холодильника Т2=275К
? Ответ выразите в градусах Кельвина.
(500К)
,
где Т1
– температура нагревателя (в градусах
Кельвина), Т2
– температура холодильника. При какой
минимальной температуре нагревателя
Т1
КПД двигателя будет не меньше 45%, если
температура холодильника Т2=275К
? Ответ выразите в градусах Кельвина.
(500К)
Решение
(задача на решение линейного неравенства)
1.
По условию КПД ≥45%.
Это означает, что
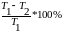 ≥45%.
Это неравенство можно немного
преобразовать: (1-
≥45%.
Это неравенство можно немного
преобразовать: (1-
 )*100≥45
или с учетом Т2=275К:
1-
)*100≥45
или с учетом Т2=275К:
1-
 ≥0,45,
≤0,55,
Т1≥
≥0,45,
≤0,55,
Т1≥
 ,
Т1≥500К.
Минимальное значение – 500К.
,
Т1≥500К.
Минимальное значение – 500К.
2. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой , где Т1 – температура нагревателя (в градусах Кельвина), Т2 – температура холодильника. При какой минимальной температуре нагревателя Т1 КПД двигателя будет не меньше 35%, если температура холодильника Т2=260К? Ответ выразите в градусах Кельвина. (400К)
1.5. Метод интервалов
Метод
интервалов – универсальный метод
решения неравенств. Он может применяться
в неравенствах, в которых правая часть
равна 0, а левая представлена (или может
быть представлена) в виде дроби или
произведения, т.е.
 или
Р(х)*Q(x)≤(≥)0
или
Р(х)*Q(x)≤(≥)0
1.5.1.Алгоритм:
1.Найти
нули числителя и знаменателя (или
сомножителей), решив уравнения

2. Нанести их на числовую ось, отметить их кратность (если (х-2)3 =0, то
число 2-корень нечётной кратности, если (х-2)6 =0, то число 2-корень чётной кратности).
3. Вычислить знак левой части на каждом из полученных промежутков, начиная со знака + и дальше расставляя с учётом кратности корней:
1) если нуль чётной кратности, то не меняя знака
2) если нуль нечётной кратности, то чередуя знаки.
4. Выбрать промежутки, соответствующие знаку неравенства: “>” - “ +”
“<” - “ - “.
5. Записать ответ.
Замечания:
1 Р(х) и Q(x) следует разложить на множители вида (х-а)к .
2. Если левая часть содержит множитель (а-х)к, то следует его заменить множителем (х-а)к с учётом кратности: т.е.(2-х)4=(х-2)4, .(2-х)3= - (х-2)3.
1.5.2.Примеры:
1.
+ - +


-5 2
3.Т.к. знак данного неравенства ˃, то выбираю промежутки, на которых знак +:
Ответ: (-∞;-5) и (2;+∞)
2.

3.
- + - +
-4 3 4
Ответ:
(-4;3]
 (4;+∞)
(4;+∞)
х3-8х2-33х≥0
Разложу на множители левую часть: х( х2-8х-33)≥0, х(х+3)(х-11) ≥0.
Нули: х=0, х=-3, х=11
- + - +
-3 0 11
Ответ: [-3;0] [11;+∞)
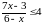
Преобразую:

Нули: 11х-27=0, 11х=27,х=

х-6=0,х=6
+ - +

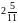 6
6
Ответ: (-∞; ] (6;+∞)
Потренируйтесь!
5. (х-2)(х-3)2(х-4)3≥0
6.
7. |
|
!!!
12.
|
|