Бұл жағдайда базистік функция ретінде келесі функциялар алынған:

Ψ_j = e ^{j kω1 t} (7.1)

(мұндай функцияларды уақыт бойынша инвариантты сызықтық жүйелерді талдауда таңдау маңызды). u(t) периодтық сигналы үшін С_K коэффициенті базистік функциялар үшін спектр деп аталынады және келесідей анықталады:

, (7.2)

мұнда k = 0, ; Т-сигнал периоды,

u(t) периодтық сигналын (7.1) базистік функцияның көмегімен көрсету, комплексті түрде Фурье қатарына жіктеу деп аталынады және келесі түрде өрнектелінеді:

Фурье қатарын тригонометриялық түрге жіктеу және келесі түрде өрнектелінеді:

немесе

,

мұнда - k- сінші гармоникалық құрамдасы, k-сінші гармоникалық құрамдастың амплитудасы, жиілігі және бастапқы фазасы;

- тұрақты құрамдасы, ол сигналдың период ішінде, сигналдың орташа мәнін өрнектейді:

, , , ,

, , .

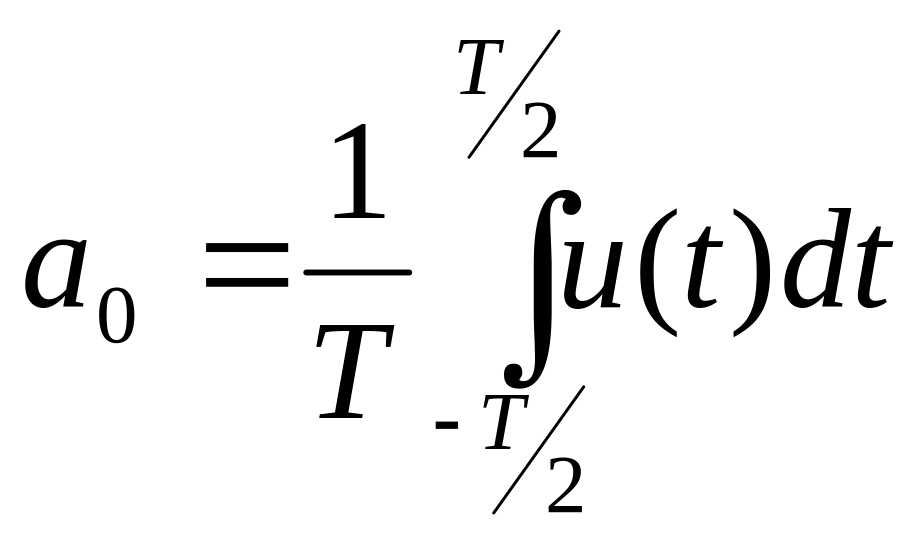- ω_k = kω₁ жиіліктің гармоникалық құрамдасының комплексті амплитудасы. a_k және b_k коэффициенттерімен келесі түрде байланысқан: .

Үздіктілік (дискреттілік) спектрлі периодты сигналдардың ерекшелігі болып табылады. Көршілес спектралды желістер арасындағы ара қашықтықтар бірдей және негізгі гармоникалық жиілікке тең.

Периодты емес сигналды, өзгеру периоды шексіздікке тең болатын периодты сигнал ретінде қарастыруға болады. Т периоды үлкейгенде, сигнал спектрінде және спектральді құрамдас амплитудалардағы аралас жиіліктер арасындағы интервал кішірейеді және шекте өте кіші шексіз шамаға айналады. Бұл жағдайда периодты сигналды спектральді жіктелуін бейнелейтін Фурье қатары, периодты емес сигналдың спектральді жіктелуін бейнелейтін Фурье интегралына түрленеді:

, мұнда (7.3)

- спектральді тығыздық

- сигналдың амплитудалық-жиіліктік сипаттамасы

- сигналдың фаза-жиіліктік сипаттамасы.

(8) өрнек Фурьенің кері түрлену формуласы деп аталынады.

Спектрлі тығыздық сигналдың уақытша функциясымен, Фурьенің төте түрленуі арқылы байланысты

Спектрлі тығыздық периодты емес сигналды бейнелейді және келесі шарттарды қанағаттандырады:

1. lim S(ω)=0

2. Спектрлі тығыздықтың модулі жұп, ал аргументі – тақ жиіліктік функция яғни:

S(ω) = S(-ω)

φ(ω) = - φ (-ω)

Сигналдарды спектрлі көрсету

Синусоидалды емес формадағы сигналды түзетін гармоникалық құрамдастардың жиынтығы осы гармоникалық емес сигналдың спектрі деп аталынады.

Спектрді спектрлі диаграмма түрінде көрсетуге болады. Осылайша нақты сигнал үшін Фурье қатарының графикалық кескінін атауға болады. Спектрлі диаграммалар амплитудалық және фазалық болып бөлінеді. Горизонтальдік осьте қандайда бір масштабпен гармоникалар жиіліктері белгіленеді, ал вертикальдік осьте гармониканың амплитудалары мен бастапқы фазалары белгіленеді.

Мысалы, егер қандайда бір периодтық синусоидалды емес сигнал келесідей қатармен сипатталса

, онда оның амплитудалы-спектрлі диаграммасын №6 суретте қараңыз, ал жиілік диаграммасын №6 ә суреттен қараңыз.