2.1. Мысалдар

Есеп № 6. B және A екі өзара байланыстағы жүйелер, бір жүйеге біріктірілген, келесі түрдегі ықтималдықтар матрицасымен берілген:

p(A,B)=

0,3 0 0 0,2 0,3 0,1 0 0,1 0

Н(A/B) толық шартты энтропиясын анықтаңыз?

Шешуі:

Берілген матрицаның жолдары мен бағандары бойынша, бірлескен ықтималдылықтардың қосындысы ретінде, шартсыз ықтималдылықтарды есептейміз:

P(A,B)=

0,3 0 0 0,2 0,3 0,1 0 0,1 0

--------------------------

p(bj) |0,5 0,4 0,1|

Шартты ықтималдылықтарды анықтаймыз және шартты ықтималдылықтар матрицасын құрастырамыз:

P(ai/bj)=

0,6 0 0 0,4 0,75 1 0 0,25 0

[0,5(0,6log₂0,6+0,4log₂0,4)+0,4(0,75log₂0,75+0,25log₂0,25)+0,1(1log₂1)]=0,485+0,324=0,809 бит/жағдай

Негізгі әдебиет: 2 [105-111]; 3[35-41]; 9[41-44]; 12[7-14].

Бақылау сұрақтары:

1. Ақпараттық теориядағы шартты энтропия түсінігі қай жерде қолданылады

2. Өзарабайланыстағы символдардың бірге пайда болу ықтималдылығын анықтау.

3. Каналдық матрица құрамын және оның қасиеттерін анықтаңыз.

4. Шартты энтропия үшін өрнекті жазыңыз және оның мағынасын түсіндіріңіз.

5. Бірнеше өзарабайланыстағы ансамблдердің энтропиясын қалай анықтауға болады.

Дәріс № 3. Ақпарат саны және артықшылық.

Үздіксіз хабарлама көзінің энтропиясы (дифференциалды энтропия) және оның қасиеттері.

Ақпарат саны дегеніміз сынақ нәтижесінде энтропияның азаюы.

Егер анықталмағандық толығымен жойылса, онда ақпарат энтропияға тең:

,

қарсы жағдайда бастапқы және соңғы энтропиялардың айырмашылығына тең:

. (3.1)

Ақпараттың ең үлкен саны максималды анықталмағандық жойылғанда - барлық оқиғалардың ықтималдылықтары бірдей болғанда анықталады

, мұнда

p – барлық оқиғалардың бірдей ықтималдықтар жағдайында іске асу ықтималдылығы.

Ақпарат артықшылығы дегеніміз ақпараттың максималды мүмкін саны мен энтропия арасындағы айырмашылық:

. (3.2)

Ақпарат дегеніміз хабарламаны қабылдағанда, алынып тасталынатын анықталынбағандық болғандықтан, ақпарат санын бір хабарламаға шаққанда, хабарламаның жалпы санының орташа энтропияға көбейтіндісі ретінде қарастыруға болады:

.

Бірдей ықтималдылық және алғашқы алфавиттің өзаратәуелсіз символдар жағдайында алфавиттің хабарламасында ақпарат саны келесідей анықталады:

(бит).

Бірдей емес ықтималдылықтар алфавиттер үшін, алфавит символына шаққанда энтропия төмендегідей:

(бит/символ),

бірдей емес ықтималдылықтар символдарынан құрастырылған хабарламада ақпарат саны келесідей

_i

Дифференциалды энтропия

Практика жүзінде ақпарат көзінің мүмкін жағдайларының жиынтығын континиум, яғни үздіксіз қайнар көздерді құрайды.

Үздіксіз ақпарат көзінің энтропиясын келесі түрде анықтаймыз: р(и) ықтималдылығының тығыздық үлестірумен сипатталатын U, үздіксіз кездейсоқ шаманың өзгеру диапазонын, Δи ені бар кіші интервалдардың п ақырғы санына бөлеміз. (u_i, u _i+ Δu) интервалына жататын и-дың кез келген мәнін іске асырғанда, U дискретті кездейсоқ шаманың, u_i мәні іске асырылады деп есептейміз. Δи кіші болғандықтан, u_i ,u_i+ Δи интервалынан и мәнін іске асу ықтималдылығы р ( u_i =<u=< u_i + Δu) төмендегідей:

Онда U дискретті кездейсоқ шаманың энтропиясын келесі түрде жазылуы мүмкін

немесе

сол себепті

онда

Δи кішіреюіне байланысты р ( u_i <u=< u_i + Δu), р(u_i) ықтималдылығына жақындай түседі оның мәні нөлге тең. Ал U дискретті шаманың қасиеті – U үздіксіз кездейсоқ шаманың қасиетіне жақындай түседі. Δu —>0 шекке көше отырып, H(U) үздіксіз қайнар көздің энтропиясы үшін келесідей өрнек аламыз:

немесе

(3.4)

Бұл шама Δu —>0 жағдайында шексіздікке ұмтылады, ол мүмкін жағдайлардың (мәндердің) шексіз үлкен саннан таңдаудың анықталмағандығы шексіз үлкен деген интуитивті түсінікке толығымен сәйкес келеді.

(3.4) қатынастың оң бөлігінің бірінші мүшесінің ақырғы мәні бар. Ол U үздіксіз кездейсоқ шаманың үлестіру заңына тәуелді және Δu кванттау қадамына тәуелді емес. Оның құрылымы дискретті қайнар көздің энтропиясының құрылымындай.

Сол қатынастың екінші мүшесі, керісінше, U кездейсоқ шаманың кванттау қадамына ғана тәуелді, осыған байланысты H(U) шексіздікке ұмтылады.

(3.4) өрнегінің бірінші мүшесін үздіксіз қайнар көздің анықталмағандығы ретінде қабылданылуы, үздіксіз қайнар көздің ақпараттық қасиетінің соңғы сипаттамаларын алу үшін бір қадамы болып табылады:

(3.5)

Ол салыстырмалы дифференциалды энтропия немесе үздіксіз ақпарат көзінің дифференциалдық энтропиясы деп аталынады (U кездейсоқ шаманың үздіксіз үлестірілуі).

Оның бірқалыпты үлестіруі бар, диапазоны бірге тең U' кездейсоқ шаманың таңдауының, орташа анықталмағандығымен салыстырғанда еркін үлестіру заңдылығы бар U кездейсоқ шаманы таңдаудың орташа анықталмағандығы ретінде қарастыруға болады .

Дифференциалды энтропия қасиеттері:

a. U кездейсоқ шама үшін оның мүмкін аумағы [α , β] жалғыз шектеуі болса, онда бұл аймақта ықтималдылықтарды бірқалыпты үлестіру, максималды дифференциалды энтропияға ие болады .

б. Егер U үздіксіз кездейсоқ шаманың мәндер аумағына шектеу болмаса, бірақ дисперсияның шектелмегені белгілі болса, онда U шаманың нормальді үлестіруі, максимальді дифференциалды энтропияға ие болады.

Негізгі әдебиет: 2[111-119]; 3[109-114]; 9[44-46].

Қосымша әдебиет: 18[34-36].

Бақылау сұрақтары:

1. Ақпарат саны түсінігі мен энтропия өзара қалай байланысқан?

2. Артықшылық түсінігін анықтаңыз.

3. бірдейемесықтималдылық символдарынан тұратын хабарламадағы ақпарат санын анықтаңыз.

4. Дифференциалды энтропияға анықтама беріңіз және оның негізгі қасиеттерін тұжырымдаңыз.

5. Қандай үлестірулер максималды дифференциалды энтропияға ие:

а) кездейсоқ шаманың өзгеру диапазонына шектеу болғанда?

в) кездейсоқ шаманың дисперсиясына шектеу болғанда?

Дәріс №4. Кездейсоқ шаманың эпсилон-энтропиясы.

Шуылы бар дискретті байланыс каналдары бойынша хабарламаны тасымалдағандағы ақпараттық жоғалтулар.

Эпсилон-энтропия

Егер:

1. Ақпарат көзінің жеке жағдайлары дегеніміз U кездейсоқ шаманың тәуелсіз іске асуы болып табылады . U кездейсоқ шаманың іске асу ансамблі р(и) ықтималдылығының тығыздық үлестіруімен баяндалады .

2. U кездейсоқ шаманың мәндерін басқа Z кездейсоқ шаманың мәндері бойынша ғана талдауға болады. Олардың айырмашылық өлшемдері берілген өндірілу нақтылығынан аспауы қажет.

3. Дәлділікке қойылатын талаптар V(Z, U) критерийін пайдалану арқылы беріледі

(4.1)

мұнда p_u(z) — шартты үлестіру тығыздығы — нақты и сигналы z сигналы түрінде шығарылуының ақиқаттық функ­циясы, ε – берілген мәннің дәлдігі.

р(и) тығыздық анықталғандықтан, (4.1) шарты орындалуы үшін р_и (z) үлестірудің шартты тығыздығы арқылы түрлендіруге болады.

Егер Z кездейсоқ шамасы U қандай да бір ε дәлдігімен кездейсоқ шаманы туындайтын болса, онда ақпарат саны U –ға қатысты Z туындау шамасында орналасып соңғы болады және келесідей анықталады:

(4.2)

мұнда p(z) = p(u)p_u(z)du — Z туындау шамасының тығыздығы.

Мүмкіндігінше қабылданатын ақпараттың ең кіші санында туындаудың берілген ақиқаттығын қамтамасыз ету. Сондықтанда p_u(z), функция жиынтығының арасынан (4.1) шартын қанағаттандыратын, I{ZU)-ң ең кішісін қамтамасыз ететін функцияны таңдау қажет.

U-ға қатысты бір Z кездейсоқ шамасында, U шамасының туындау дәлдігіне қойылатын талаптар қанағаттандырылса ең кіші ақпарат саны U шамасының ε (эпсилон) - энтропия шамасы деп аталынады және Н_ε(U) деп белгіленеді:

егер

(4.3)

Аталмыш шаманың маңыздылығы, ε (эпсилон) – энтропия - берілген нақтылықпен (дәлдікпен) хабарламаны шығару үшін ең кіші екілік сандарды тасымалдау болып табылады.

ШУЫЛЫ БАР БАЙЛАНЫС КАНАЛДАРЫ АРҚЫЛЫ ХАБАРЛАМАНЫ ТАСЫМАЛДАҒАНДА АҚПАРАТТЫҚ ЖОҒАЛТУЛАР

Кедергі болған жағдайда A хабарлама ансамбліне қатысты B қабылданған хабарлама ансамблінде орналасқан орташа ақпарат саны (немесе шуылы бар канал бойынша бір символмен таралатын орташа ақпарат саны) келесідей анықталады:

а) бірігу энтропияның көмегімен:

I(A,B)=H(A)+H(B)-H(A,B) (4.4)

б) шартты энтропияны пайдалану арқылы:

I(A,B)=H(A)-H(A/B) (4.5)

Өрнектің мағынасы келесідей: H(A) шамасы - ол қайнар көздің энтропиясы, ал H(A/B) шамасы-каналдағы қатенің нәтижесінде жоғалған орташа ақпарат саны.

I(A,B)=I(B,A) (4.6)

(4.4)- формуладан қорытылған (4.5) формуланы пайдалану ыңғайы:

(4.7)

Негізгі әдебиет: 1[75-76]; 2[125-128]; 6[137-139].

Қосымша әдебиет: 13[144-147]; 18[42-57].

Бақылау сұрақтары :

1. Эпсилон-энтропия кездейсоқ шаманың маңыздылығы қандай?

2. Туындаудың ақиқаттылығының орташаквадраттық критериін сипаттаңыз.

3. Біріктіру энтропиясының көмегімен жіберілген хабарламаға қатысты, В қабылданған хабарламадағы ансамблге тиісті кедергі жағдайындағы ақпараттың орташа санын анықтау.

4. Шартты энтропия көмегімен жіберілген хабарламаға қатысты, В қабылданған хабарлама ансамбліне тиісті орташа ақпарат санын кедергі жағдайында анықтау.

5. Шуылы бар байланыс каналдары бойынша хабарламаны тасымалдағанда ақпараттық жоғалтулар қалай анықталынады.

Дәріс №5 Ақпаратты тасымалдау жылдамдығы және байланыс каналдарының өткізгіштік қабілеті.

Кедергі болмаған жағдайда ақпаратты тасымалдау жылдамдығы уақыт бірлігінде хабарлама санымен анықталады және келесі өрнекке тең

(5.1)

n – уақыт бірлігінде хабарлама көзімен өндірілетін символдар саны

H –хабарламаның бір символын қабылдағанда алынатын энтропия.

Тасымалдаудың техникалық жылдамдығы

( симв/сек ) , (5.2)

мұнда - екінші алфавиттің бір символының тасымалдау уақыты .

Осылайша, бірдей ұзақтығы бар, бірдей ықтималды, өзараықтималды символдардан құрастырылған хабарлама үшін , ақпаратты тасымалдау жылдамдығы келесідей:

( бит/сек ).

Ұзақтығы бірдей, бірдейықтималды жағдайда ақпаратты тасымалдау жылдамдығы келесідей:

( бит/сек )

Өткізгіштік қабілет дегеніміз (немесе байланыс каналының көлемі), аталмыш байланыс каналы бойынша ақпаратты тасымалдаудың максимальді жылдамдығы:

( бит/сек ).

Екілік код үшін:

( бит/сек ).

Кедергі болған жағдайда байланыс каналының өткізгіштік қабілеті секундына қабылданған белгілер санының қабылданған сигналға қатысты, хабарлама көзінің энтропиясының және хабарлама көзінің шартты энтропиясының айырмашылығының көбейтіндісіне тең:

немесе

]

Мысалы

Есеп №8

Хабарлама екілік кодта тасымалданады (m=2) 0-дің тасымал уақыты t₀=1 сек, 1-ге сәйкес импульс ұзақтығы t₁=5 сек. Егер 0 символының пайда болу ықтималдылығы p₀=0,37,1 символының пайда болу ықтималдығы p₁=0,63 болса, ақпаратты тарату жылдамдығын анықтау.

Шешуі:

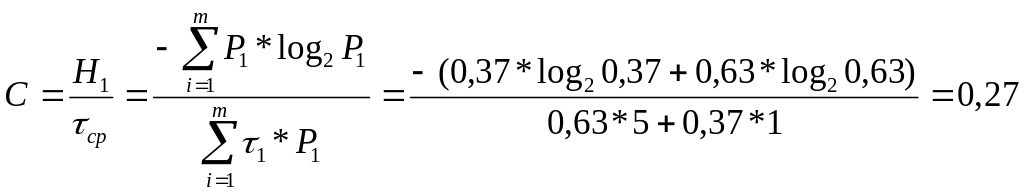Есеп № 9

A және B екі жүйе үшін, егер екі жүйенің сипаттамасының A жүйесінің шығысында сигналдардың пайда болуының шартты емес ықтималдығы ғана белгілі болса, байланыс каналының өткізгіштік қабілетін анықтау қажет:

р(а1)=0,1; р(а2)=0,4; р(а3)=0,5

және шартты ықималдықтар матрицасы келесідей:

p(b/a)=

1 0 0 0,25 0,75 0 0 0,2 0,8

Әрбір хабарлама символы 0,1 сек-та өңделінеді.

Шешуі:

Бірлескен оқиғалардың ықтималдық мәнін анықтаймыз және AB біріктірілген жүйелер үшін ықтималдықтар матрицасын құрастырамыз:

p(a1,b1)=p(a1)*p(b1/a1)=0,1*1=0,1

p(a2,b1)=p(a2)*p(b1/a2)=0,4*0,25=0,1

p(a3,b1)=p(a3)*p(b1/a3)=0,5*0=0

p(a1,b2)=p(а1)*p(b2/a1)=0,1*0=0

p(a2,b2)=p(a2)*p(b2/a2)=0,4*0,75=0,3

p(a3,b2)=p(a3)*p(b2/a3)=0,5*0,2=0,1

p(a1,b3)=p(a1)*p(b3/a1)=0,1*0=0

p(a2,b3)=p(a2)*p(b3/a2)=0,4*0=0

p(a3,b3)=p(a3)*p(b3/a3)=0,5*0,8=0,4

P (A,B)=

0,1 0 0 0,1 0,3 0 0 0,1 0,4

P (a1) = 0,1 P (a2) = 0,4 P (a3) = 0,5

P (b₁) = 0,2; P (b₂) = 0,4; P (b₃) = 0,4

p(a/b) түріндегі шартты ықтималдықтарды табамыз:

P(a/b)=

0,5 0 0 0,5 0,75 0 0 0,25 1

Негізгі әдебиет: 2[141-147]; 4[33-36]; 6[140-142]; 8[63-79]; 10[18-21].

Қосымша әдебиет: 13[139-141].

Бақылау сұрақтары:

1. Тасымалдың техникалық жылдамдығы түсінігін анықтаңыз.

2. Ақпаратты тасымалдау жылдамдығы түсінігін анықтаңыз.

3. Каналдың өткізгіштік қабілеті түсінігінің мағынасын түсіндіріңіз.

4. Кедергісі бар және кедергісі жоқ дискреттік каналдың өткізгіштік қабілетінің өрнегін жаыңыз.

Дәріс №6. Сигнал түсінігі және оның моделдері. Детерминдік сигналдарды көрсетудің уақытша формасы.

Сигнал дегеніміз – ақпараттық жүйеде хабарламаны тасымалдау үшін арнайы жасалынған, ақпаратты, материалды тасушы.

Ақпаратты тасушы ретінде тербеліс қолданылады.

Детерминдік тербеліс кез-келген уақыт аралығында анықталынады.

Кездейсоқ тербелістердің, мәнін болжауға мүмкін емес параметрлері болуы мүмкін.

Сигнал кездейсоқ тербелісті білдіреді.

Детерминдік сигналдардың моделдерін оқып үйрену қажет:

1) Себебі кездейсоқ процесс детерминдік функцияның жиынтығы түрінде болуы мүмкін.

2) Детерминдік сигналдар ақпараттық техника объектілерін өлшеу, жөндеу, реттеу мақсатында арнайы құрастырылады.