Ықтималдылық және ақпарат.
Ықтималдылық тұрғыдан ақпаратты кездейсоқ оқиғаның шығуы туралы хабарлама ретінде, кездейсоқ шама мен функцияның іске асыруы ретінде қарастыруға болады. Ал ақпарат саны аталмыш оқиғалардың, шамалардың, функциялардың априорлық ықтималдықтарына тәуелді етеді.
Оқиғаларды сынақтардың мүмкін шығарылымдары ретінде қарастыруға болады. Барлық шығарылымдар ансамблді, яғни оқиғаның шығарылым тобын құрайды.
Өлшенілетін шаманың мәні U1, U2, …, UN
Ықтималдылықтар р1, р2, …, рN
Энтропия
Шеннон энтропияны N ансамбілінен дискреттік қайнар көздің жағдайының анықталмаған таңдауының өлшемі ретінде анықтады
(1.1)
Оны қайнар көздің жағдайына қатысты анықталмағандықты толығымен жойғанда алынатын ақпарат санының шамасы ретінде де қарастыруға болады.
(1.1) -дегі логарифмнің негізгі өлшем бірлікті анықтайды. Негізгі 2 болғанда бит, негізі 10 болғанда– дит, негізгі e болғанда – нат өлшем бірлігі болады.
Қайнар көздің тең ықтималдылықты жағдай кезінде Шеннон формуласы келесі түрде болады:
- Хартли формуласы
.
(1.2)
Энтропия қасиеті
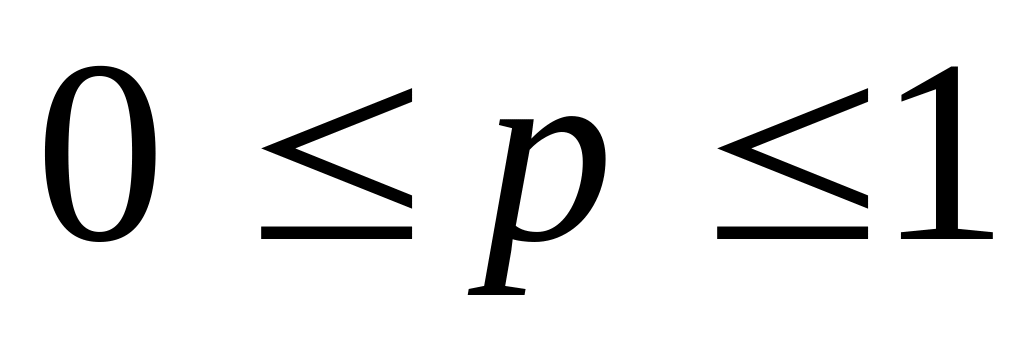интервалында
үздіксіз,
яғни р- ң кіші өлшемдерінде H шамасы
аз өзгереді.
, p-ға қатысты симметриялы, яғни
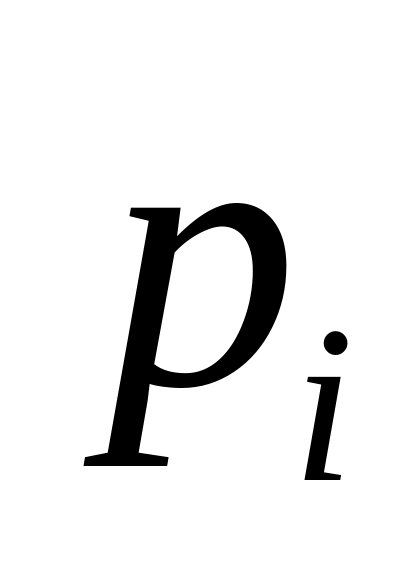-ң
аргументінің кез-келген ауысуында
өзгермейді .
Егер
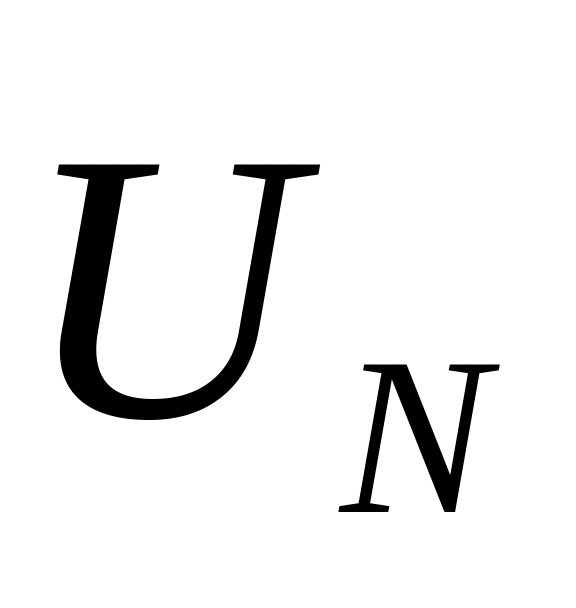оқиғасы екі
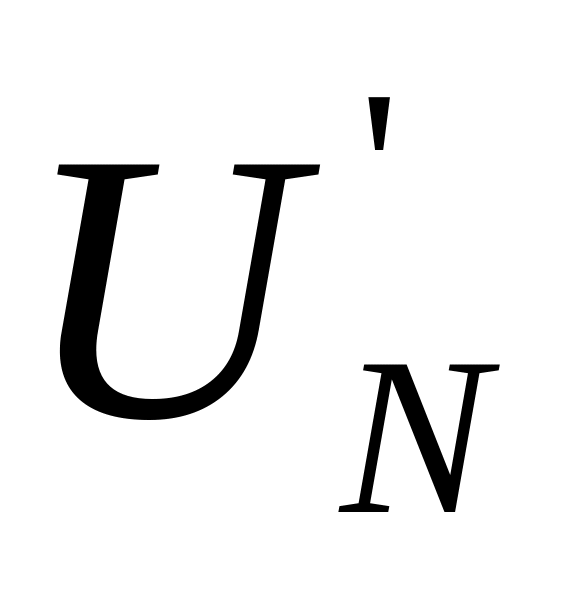және
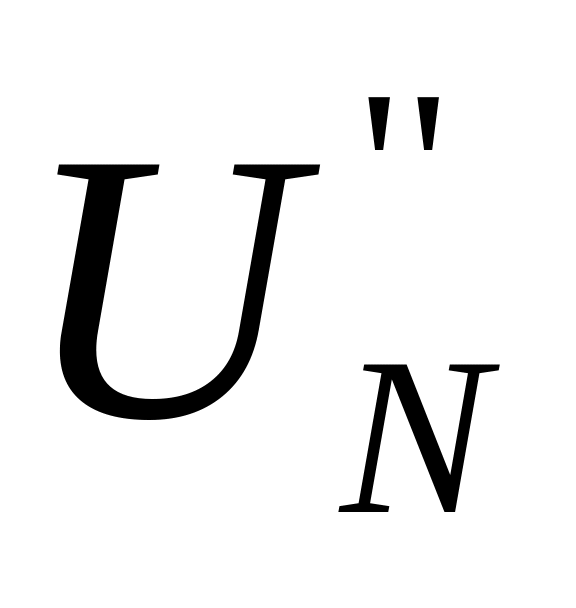оқиғалардан тұратын, ықтималдылықтары
және
,
,
онда
Энтропия әрқашан теріс емес.
Оқиғалардың біреуінің ықтималдылығы бірге тең болса, энтропия нөлге тең.
Барлық ықтималдылықтар өзара тең болғанда энтропияның мәні ең үлкен болады.
,
мұнда
.
Э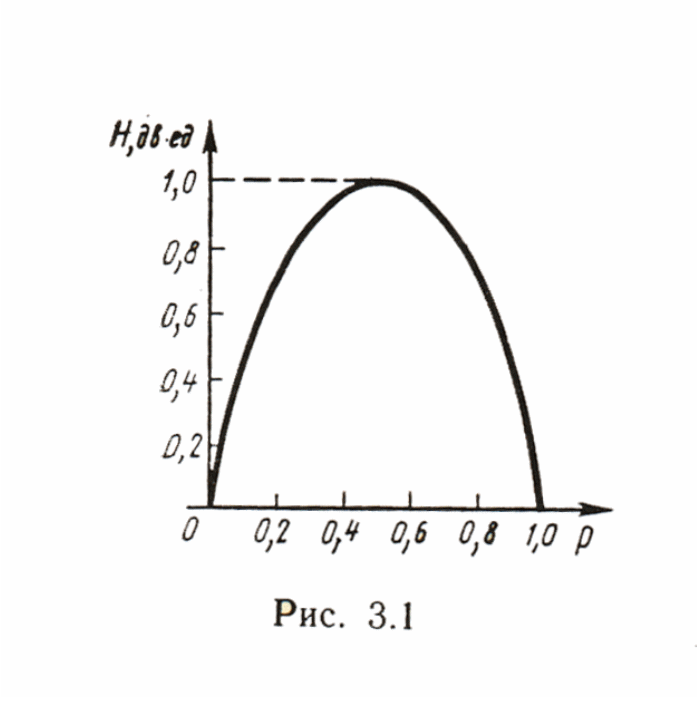
нтропия
ансамблден бір жағдайды таңдаудың
орташа анықталмағандығын
сипаттайды
және тек қана ықтималдылық жағдайлармен
анықталынады.
Мысал. Екі дискретті кездейсоқ шаманың U және V ансамблдері берілген
Негізгі әдебиет: 2 [97-106]; 3 [12-15]; 5 [7-9]; 9[31-40].
Қосымша әдебиет: 16 [15-25]; 17[5-30], 7[3-9].
Бақылау сұрақтары:
1. Ақпараттар теориясының негізгі міндеттерін анықтаңыз.
2. Байланыс жүйесі ұғымын анықтаңыз.
3. Ақпараттың негізгі өлшемдерін атаңыз.
4. Энтропия түсінігін анықтаңыз.
5. Энтропияның негізгі қасиеттерін атаңыз.
Дәріс №2. Шартты энтропия мен біріктіру энтропиясын анықтау.
Ақпараттар теориясында шартты энтропия түсінігі төмендегідей өзара байланысты анықтағанда қолданылады:
а) кодталатын алфавит символдарымен (бір қайнар көзбен тізбектеліп таңдалатын жағдай арасындағы).
ә) байланыс каналдарымен ақпаратты тасымалдағанда жоғалтуларды анықтау үшін.
б) біріктіру энтропиясын есептеу үшін.
Егер i - хабарлама көзінің еркін түрдегі жағдайы болсын, j - адресаттың еркін түрдегі жағдайы, онда дербес шартты энтропия A қайнар көздің әрбір і-ші жағдайында шартты энтропиясын анықтайды және келесі формуламен есептелінеді:
(2.1)
Жалпы В шартты энтропия A хабарламасына қатысты A таратылатыны белгілі болса, B қабылдағыштағы ақпарат санын сипаттайды, (немесе, A ансамблдің жағдайы белгілі болғанда, В ансамблінің бір жағдайына шаққанда орташа анықталмағандық).
(2.2)
Қасиеттері: А және В екі ансамблдерді біріктіру үшін
H(B/A)≤H(B) и H(A/B)≤H(A).
Жалпы жағдайда егер біз A-ң m сигналдарын тасымалдап және В –ң m cигналдарын алуды күтетін болсақ, онда байланыс каналында кедергілердің әсері толығымен келесі түрдегі каналдық матрицамен баяндалады:
а/в |
B1 |
b2 |
…. |
bj |
… |
bm |
а1 |
P(b1/a1) |
P(b2/a1) |
… |
P(bj/a1) |
… |
P(bm/a1) |
а2 |
P(b1/a2) |
P(b2/a1) |
…. |
P(bj/a2) |
…. |
P(bm/a2) |
…. |
…. |
…. |
….. |
…. |
…. |
… |
аi |
P(b1/ai) |
P(b2/ai) |
…. |
P(bj/ai) |
…. |
P(bm/ai) |
… |
…. |
…. |
….. |
…. |
…. |
…. |
аm |
P(b1/am) |
P(b2/am) |
….. |
P(bj/am) |
….. |
P(bm/am) |
Диагоналдар бойынша орналасқан ықтималдылықтар дұрыс қабылдауды анықтайды да, қалғандары – жалған.
Каналдық матрицаның колонкаларын толтыратын цифрлардың мәні, әдетте негізгі диагоналдан қашықтаған сайын кемиді және кедергінің болмаған жағдайында негізгі диогоналда орналасқандардың барлығы, цифрдан басқаларының бәрі нөлге тең болады.
Бірігу энтропиясы және статистикалық тәуелді хабарламалардың бірге пайда болу энтропиясын есептеу үшін қолданылады. А хабарламасын жіберу ансамблі үшін және В қабылдау ансамблі үшін бірігу энтропиясы келесідей:
бит/екі
символ (2.3)
Тәуелсіз ансамблдер болған жағдайда:
H(A,B)=H(A)+H(B)
Бірігу энтропиясы және шартты энтропия өзара келесідей қатынаспен байланысқан:
H(A,B)=H(A)+H(B/A)=H(B)+H(A/B) (2.4), Біріктіру энтропиясы келесі түрдегі матрицаның көмегімен есептелінуі мүмкін:
P(a1,b1) p(a1,b2) . . . p(a1,bm)
P(a2,b1) p(a2,b2) . . . p(a2,bm)
P(ai,bj)= . . . . . . . . . . . .
P(am,b1) p(am,b2) . . . p(am,bm)
Матрица қасиеттері:
,
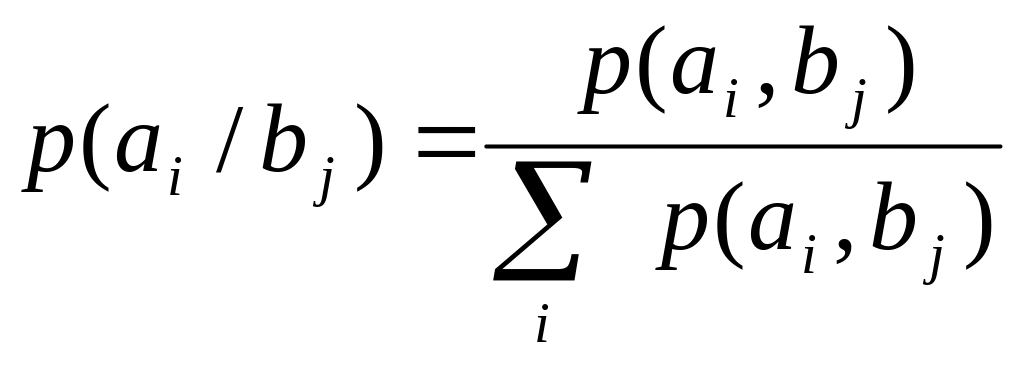