Дәріс №14. Ақпаратты кванттау

X, T жинақталған координаталар жүйесіндегі үздіксіз сиганалдар үздіксіз функциялармен x(t) белгіленеді. Ұқсас көрсететін сигналынан цифрлыққа өту сигналдың уақыт және деңгейі бойынша квантталуымен (дискретизациясымен) x(t) байланысты.

Ақпаратты беру, сақтау және өңдеу үшін қолданылады.

Дискретизация әдістерін классификациялау.

Дискретизация әдістерін келесі белгілермен өтуі мүмкін.

* уақыт бойынша кванттау – дискретизация;

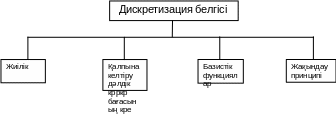
1. есептеу жиілігі;

2. дискреттеу және қалпына келтіру дәлдік бағасының критерий;

3. базистік функциялар;

4. жақындау принципі;

Өлшеу жиілігі

Өлшеу жиілігі бойынша дискреттеу әдісі бірқалыпты және бірқалыпсыз болып бөлінеді.

бірқалыпты

бірқалыпсыз

(адаптивті және программаланған).

Адаптивті әдіс үшін интервалы сигналдарды беру параметрлерінің ағымдық өзгерумен тәуелді өзгереді. Программаланған әдістер үшін интервалының өзгеруі (F₀ сұранысының жиілігі) түскен ақпаратты талдау негізіндегі оператормен, немесе алдын ала орнатылған программалық жұмыспен сәйкес өндіріледі.

Дәлдік бағасының критерисі

x(t) сигналының мәні, V(t) туынды функция, сонда (t) дискретизация ағаттығы немесе сәйкес қалпына келтіру:

Ағаттық бағасы жеке және көпше сигнал беруде өндіріледі.

Көп жағдайда туынды функциясының V(t) интегралында x(t) сигналынан ауытқуы келесі критериілермен бағаланады.

1. Көбірек ауытқу критериі

1. 

2. Орташа квадратты критериі

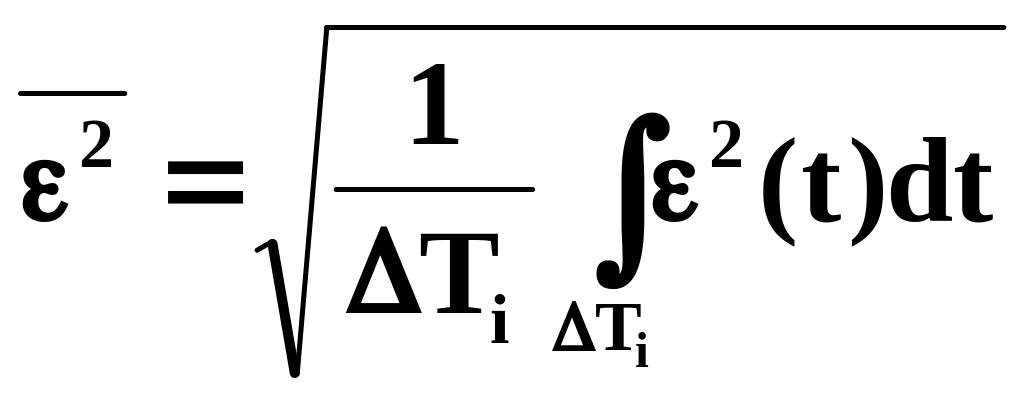
3. V(t) – дан x(t) ауытқу шарасы тәрізді интегралдың критерий келесі түрде болады:

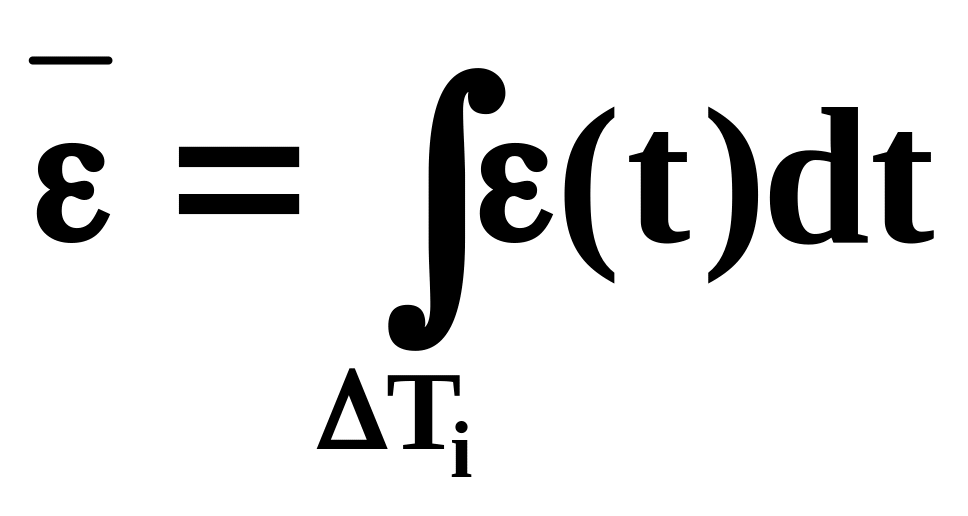
4. Ықтималдық критерисі қатынасымен анықталады.

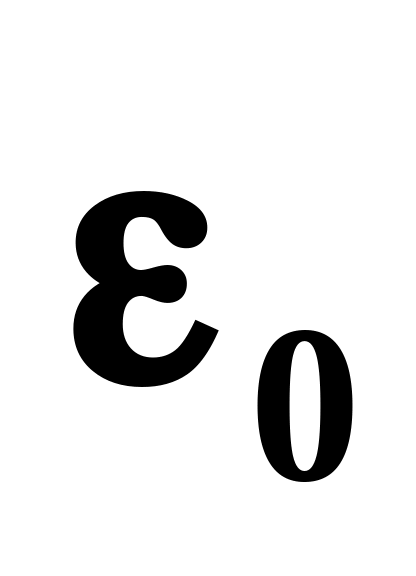5. – ағаттықтың берілген мәні;

p₀ – ағаттықтың мәнін асып кетпеу мүмкіндігінің ықтималдығы.

2) Базистік функциялар

Дискреттеу есебінің түсіндірмесі келесідей: [a,b] кесіндісінде анықталған, R функциясының класына жататын, берілген x(t) үшін, [a,b] кесіндісінде t_i бөлігінде нүктелер саны минимальды немесе болатын p(t) функциясын немесе V(t) S табу керек (мұндағы S – функцияның кейбір тұрғызылған класы), мұнда - ағаттықтың жіберілген мәні, - алынған P(t) критериімен жақындалған, сәйкес V(t)-дан x(t) ауытқу бағасы.

Базистік типін таңдау.

Базистік функциялар типін таңдау негізінен дискреттеу құрылғысының қиындық шектелуінің талап етілуімен және сигналды қалпына келтірумен анықталады. Алғашқы сигналды қалпына келтіру үшін x(t) таңдалуының жиынтығы кейбір көпмүшелерге сәйкес қойылады.

t_i есептеу нүктесіндегі мән x(t) функциясының мәнімен сәйкес келеді.

V(t) туынды функциясы көбіне жақындағылармен сәйкес келеді, жалпыжағдайда олардан ерекшеленуі де мүмкін.

Дискреттеу есебінде қолданылатын функциялардың негізгі типтері: Фурье қатары, Котельникова қатары, Чебышева полиномы, Лежандра полиномы, дәрежелі полиномы, Уолта функциялары, Хаара функциясы, гипергеометриялық.

4. Жақындау принципі

Жақындау принципі бойынша әдістердің үш тобын бөліп алуға болады:

– интерполяциялық;

– экстраполяциялық;

– комбинациялық;

Экстраполяциялық әдістерін дискреттеу үшін сигналдың кідіруін талап етпейді, яғни нақты уақытта жұмыс істейтін, басқарушы жүйелерде қолданылуы мүмкін.

Интерполяциялық экстраполяциялық әдіспен салыстырғанда аралық есептеуді азайтуға қамтамасыз етеді, бірақ интерполяция интервалында сигналдың кідіруін талап етеді.

Интерполяциялық-экстрополяциялы әдістер үшін p(t) жақын функциясын табу процедурасы екі этапқа бөлінеді. Бірінші этапта интерполяция әдістері болып бастапқы бөлігі үшін P(t) жақындатылған функциясы табылады. Екінші этапта табылған функция мәні үшін энтрополяцияланады және бұл функциядан сигналдың ауытқуы тексеріледі.

Дискреттеу қадамын таңдау үшін сигналдардың әртүрлі моделдері қарастырылады және сәйкес есептеу критерилері енгізіледі.

1. Санақ арасындағы интервал дисскреттелген сигналдың жиілік спектрі есебімен таңдалатын жиілік критерисі;

2. Корреляциялы сигнал интервалдарымен санап шығарулар арасындағы интервалдар байланысын орнататын санап шығарудың корреляциялы критериі;

3. Сигналдың детерминиралды моделі үшін берілетін және сигналдың деңгейі мен бірінші туындысы бойынша квантты саты мәнімен санақ арасындағы интервалдар тәуелділігін орнататын, санап шығарулардың квантты критериі;

Котельников теоремасы бойынша санақ шығарудың жиілігін таңдау.

Котельниковпен шектелген спектрімен функция үшін теорема дәлелденген. Егер x(t) үздіксіз функция Дирихле шарттарын (үзім-үздіксіз шектелген және экстремумдарды соңғы санымен тұрады) қанағаттандырады және оның спектрі кейбір f_m жиілігімен шектелген болса, онда F₀=2f_m, мұндағы: f_m - (x(t) сигналының S(j ) спектріндегі максималды жиілік, функциясымен алынған, өз мәнінің дискретті жиынымен толық анықталады. Бұл жағдайда, функция x(t) - таңдауының нақты мәндері бойынша ағаттық мына түрде қалпына келтірілуі мүмкін:

, (*)

мұндағы:

Интерполяциялық қатар Котельников қатары деп аталады.

(*) дан шығатыны, шектелген жиілік спектрімен тұратын x(t) функциясы әрбір қосылғыш мына функция мұндағы мына түрде өрнектеліп қосынды (шексіз) түрінде қажеттеледі.

үшін қосынде (*) әрбір k–ші уақыт кезінде тек бір k–ші қосылғышпен анықталады, өйткені барлық қалған қосылғыштар бұл уақыт аралығында нолге айналады.

x(t) нақты іске асыруды теориялық қалпына келтіру процедурасы оның санап шығарылуы бойынша келесідей келтіріледі. Бастапқы үздіксіз функцияның x(t) қайта жіберілетін жағында уақыт интервалы арқылы x(t_i) лездік мәні анықталады және байланыс каналына A_i амплитудасымен импульсі түрінде және x(t_i) – ге тең, A_i , ауданы бар, шексіз аз ұзындықта беріледі, қабылдау жағында мұндай импульстар тізбегі қию жиілігі f_m - ге тең, төменггі жиіліктің фильтрі арқылы жіберіледі.

Бірқалыпты дискретизация үшін қадам және F₀ есептеуішінің жиілігі тұрақты шамалар болып табылады. t_i санап шығу нүктесі бұл жағдайда бірқалыпты t өсі бойынша орналасқан.

Дискретизация сигналы арқылы өтетін құрылғы дискретизатор деп аталады.

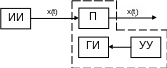
ГИ – импульстер генераторы;

П – қайта құрушы;

УУ – басқару құрылғысы;

ИИ – ақпарат көзі.

Импульстар генераторы x(t_i) сигналын таңдаудың кейбір дискретті тізбегін үзушіге шығарады. Генератордан түсетін импульстар генераторының жұмысы басқару құрылғысымен анықталады.

Ақпарат тасушылар болып табылатын нақты сигналдар ақырғы ұзындықтан тұрады, ол шексіз спектр дегенді білдіреді.

Практикадан санап шығару жиілігі көбіне мына формула бойынша анықталады:

, мұндағы: k₃ – қор коэффиценті, көп жағдайда

Деңгейі бойынша кванттау.

Деңгейі бойынша сигналдың кванттауы x(t) дискреттікте t_i санап шығару кезінде x(t_i) сиганалының үздіксіз мәніне өзгеруінен тұрады. Деңгейі бойынша кванттау бірқалыпты және бірқалыпсыз болуы мүмкін.

Дискретизация жиілігі (sampling rate) – бұл килогерцте өрнектелген (килогерц – секундына 1000 таңдау), секундына ұқсас - цифрлар (таңдау) өзгерулерінің саны.

Көбіне қолданылатын жиіліктер 11,025; 22,05; және 44,1 кГц Audio CD-да 44,1 кГц дитскретизациялы жиілік қолданылады, ол дыбыстық жиілік 22,05 кГц – не дейін туындауына мүмкіндік береді. (1/2 дискретизация жиілігі) туынды және 44,1 кГц дискретизация жиілікті 16 разрядты (яғни екі байтты) стереодыбысты жазбасы секундына 2x44100x2=176200 бұл мән 176, 2 кб/с байт өңдеуді талап етеді, 150кб/с біркелкі жылдамдықтағы CD–ROM дисководта мәліметтер беру жылдамдығы асып түседі.

Негізгі әдебиет: 2[63-93]; 5[46-50]; 8[35-40,44-47]; 9[60-93].

Қосымша әдебиет: 13[50-58].

Бақылау сұрақтары:

1. Дискретизация мен кванттау процестерінің мәні неде?

2. Дискретизация есебінің жалпы берілгенін түсіндіріңіз.

3. Сигналды қалпына келтіру орташаквадратты критерисі деп нені түсінуге болады?

4. Котельников теоремасын түсіндіріңіз.

5. Кванттау шумы деген не?