Основными
критериями работоспособности подшипников
качения,
применяемых в шпиндельных
узлах станков, являются точность
изготовле-
ния, радиальная и осевая
жесткость, радиальная и осевая несущая
способ-
ность, быстроходность, момент
трения, нечувствительность к перекосам.
По
данным А.М. Фигатнера /12/, в качестве
характеристики работо-
способности
шпиндельных опор качения для станков
с максимальным диамет-
ром обрабатываемых
деталей 400-800 мм принимают следующие
показатели:
Κι
= Ί^Ιj[/
, Вт/мм;
Kg = ' »
мм/мин;
ы
. , cl
■ П
w
ах
,
Кз
= JV/d
, Вт/мм;
К4
= ^5 ,
мм/мин,
где
/1/ - мощность привода, Вт;
И.
мах-
наибольшая частота вращения шпинделя,
мин-1;
Ci
- диаметр
шпинделя в передней опоре, мм;
D
-
максимальный диаметр обрабатываемой
детали, мы.
Показатели
Kj и
Кз характеризуют среднюю нагруженность
шпиндель-
ных узлов станка, a
Kg и К4
- их быстроходность.
Расчетную
долговечность подшипников качения
шпиндельных узлов
можно определить
по формуле ,а/.
/ (с/а)
ю6
номинальная
долговечность, ч;
динамическая
грузоподъемность, Н (кгс);
эквивалентная
нагрузка Н (кгс); ,
частота
вращения подвижного кольца, мин-·*·.
Для
определения С
следует пользоваться формулами для
расчета
долговечности L
(млн.оборотов)
по ГОСТ 18855-73 или /4/.
Для
обеспечения высокой точности вращения
шпиндели устанавливают
в подшипниках
повышенных классов точности: высокий
(5 кл.), прецизион-
ный (4 кл.),
сверхпрецизионный (2 кл.).
В
табл. 7.2 приведены рекомендуемые классы
точности подшипников
для шпинделей
станков /7/.
С
а
377.2. Шпиндельные опоры ;
~ 6On ’
п
н |
4 (СА) |
5 |
5 (А) . |
п |
4 (С) |
5 |
5 (А) |
в |
2 (выше С) |
4 (С) |
4 (С) |
А |
2 (выше С) |
2 (выше С) |
2 (выше С) |
С |
2 (выше С) |
2 (выше С) |
2 (выше С) |
Геометрические
погрешности подшипников с точностными
требованиями выше класса С должны быть
в пределах 1-2 мкм, волнистость беговых
дорожек колец 0,1-0,2 мкм, а разномерность
и некруглость тел качения примерно
0,3 мкм.
Значения
допускаемых радиального биения
внутреннего кольца радиальных и
радиально-упорных шариковых и роликовых
подшипников-в ГОСТ 520-71.
Расчет
конструктивных параметров шпиндельных
узлов
Расчет
двухопорного шпинделя на радиальное
биение
Точность
вращения шпинделя характеризуется
радиальным и осевым биением его переднего
конца и регламентируется стандартами
в зависимости от класса точности
станка. В среднем радиальное и осевое
биение рекомендуют ограничивать в
пределах одной трети от допуска на
размер детали
Радиальное
биение Δ
переднего
конца двухопорного шпинделя зависит
от эксцентриситета подшипников в
передней и задней dTg
опорах,
размеров консоли шпинделя а и межопорного
расстояния L,
Рис.
7.1. Схемы радиального биения переднего
конца шпинделя
38
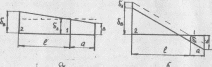
Если
радиальные биения в передней и задней
опорах имеют одинаковые знаки и
лежат в одной плоскости, то согласно
рис. 7.1,а:
Sa
-
Л _ JL
е
’
Отсвда
&
й - сГй
Δ
= А
где
Од,
0$ -
радиальные биения переднего (заднего)
подшипника.
Если
радиальные биения в опорах имеют
разные знаки (противополож-
ные
направления), (рис. 7.1,6), то
Δ
=
Λ
+
f-
(cQ
+
cfA
).
Если
в передней опоре шпинделя установлено
3L,
подшипников,
а в
задней .опоре %
подшипников, то радиальное биение А
определяется
по
формуле
Δ
~ Ί,5 |
0а |
_д_)1 |
1 ι/Γ -1 |
/г; |
\Г2г/J |
При
условии одинаковых биений передней
и задней <fg
опор
для
определения
А и А пользуются формулами
%
5
CL
+ e >
WB-
3
l
Допускаемые
ГОСТ 520-71 значения радиального биения
внутреннего
а
кольца
радиальных и радиально-упорных
шариковых и роликовых подшипников
приведены в табл. 7.3.
Таблица
7.3
Допускаемые
значения радиального биения |
Допускаемое радиальное |
биение, мкм |
|
||
диаметр q[, мм j |
0 |
! 6 |
! 5 |
4 ! |
2' |
30 |
13 |
10 |
10 |
5 |
3 |
30-50 |
15 |
12 |
10 |
5 |
3 |
50-80 |
20 |
16 |
12 |
6 |
4 |
80-120 |
25 |
20 |
14 |
7 |
5 |
.120-180 |
30 |
24 |
16 |
8 |
6 |
РАСЧЕТ
ПЕРЕДАЧИ ВИНТ-ГАЙКА КАЧЕНИЯ
Конструирование
новых, прогрессивных типов станков с
ЧТО связано с повышенными требованиями
к приводу подач. Постоянное ужесточение
норм точности обработки предопределяет
повышение требований к жесткости и
демпфирующим свойствам всей несущей
системы станка, а также к точности
шпинделей и тяговых устройств.
39
В
станках с ЧПУ особенно широкое применение
в качестве тягового устройства нашла
передача винт-гайка качения. Ее
достоинства: малое трение, отсутствие
зазоров и возможность создания
предварительного натяга, высокая
жесткость и достаточная для многих
случаев долговечность.
Исходными
данными для расчета являются выбранные
из конструктивных соображений
следующие параметры:
/Т7
- масса перемещаемых частей механизма
подачи, Н·с^/см; t
- длина
винта, см.
Основы
расчета
Для
обеспечения точности обработки заготовки
по контуру на станке
с ЧПУ согласно
исследованиям, пров,еденным ЭНИМС,
необходимым является
условие, при
котором собственная частота колебаний
привода подачи стан-
ка не превышает
60 Гц Л/.
Эта
частота рассчитывается
по зависимости
/r
JT
\! 1Гм Ъ
ЬО I ц ,
где
S
-
податливость
механизма подает
,
Н/см^;
УУ!
- масса исполнительного механизма, Н с
/см.
В
свою очередь податливость механизма
подачи не должна превышать
значения
cf
F
7
· Ю
т
-е
сЧн
В
процессе работы механизма его жесткость
снижается, поэтому податливость следует
принимать не менее чем с двойным запасом,
т.е.
6
3,5-Ю~
т
(8.1)
Податливость
шариковой винтовой передачи складывается
из двух параметров-податливости,
вызванной контактной деформацией тел
качения, и податливости винта, вызванной
деформацией растяжения - сжатия.
.
Суммарная, податливость передачи /3/
ll_
+ J-
,
Vd^H
■
Ерасч
EF
где
d-ι
- диаметр
шарика, см; ^
ϊραα~
Расче™°®
число шариков передачи ( Еращ-О,7£);
£ -
длина винта, см;
р
- площадь поперечного сечения винта,
см'';
£ -
модуль упругости, Н/см^;
Ри -
сила натяга передачи, Н.
40
Подставляя
значения ?.ра.сч,
F
и принимая
среднюю силу натяга,
равную 150 Н,
можно значение податливости записать
в виде следующей
эмпирической
зависимости:
где
do
-
диаметр винта, см.
Подставив
значение (8.2) в уравнение (8.1), получим
окончатель-
ную
формулу для определения параметров
передачи:
У,/4
· VdJ
, Q,i7l
ojm
(
-
НО.
(8.3)
do
— Ί,6όίι do
Это
уравнение позволяет вычислять параметры
винта-гайки качения
в соответствии
с нормалью Н 23-7. При соответствующей
проработке и
составлении блок-схемы
параметры передачи можно вычислять
при помощи
ЭВМ (рис. 8.1).
Расчет
производится в следующей последовательности:
Г1о
конструктивным соображениям назначают
такие параметры:
/Т?
- массу перемещаемых частей механизма
подачи, Н-с^/см; £ - длину
винта, см.
Определяют
значение диметра винта:
cLo^^o’
которое
округляется до целого значения по
табличным данным нормали
Н 23-7 (табл.
8.1).
Как
видно из табл. 8.1, одному значению do
соответствует
несколь
ко значений ~t,
и di
·
Вначале
выбирают их меньшее значение и.
подставляют в зависимость
(8.3). Если
условие не выполняется, то выбирают
большие значения и
снова проверяют
его выполняемость. Если все значения
di
для
рассчи-
танного do
обеспечивают
соблюдение условия (8.3), то
конструктивно
принимают большее
значение согласно нормали Н23-7 (см. табл.
8.1) и
повторяют процедуру до тех пор,
пока условие (8.3) не будет выполнено.
Затем
рассчитывают необходимое число рабочих
шариков в передаче:
do
iw
Рассчитанные
таким образом
при выполнении
графической части.
41o,sr
f-er
.
(8.2)do
—
У,6
di do
dLtdo
,oLi
, i-,
2.
pcLd.
используют
Расчеты. CLa .СМ |
Шриним. Шаг вин-!Диам.ша- ! Hr, ,см!та £,см!рика d, |
■ ! Расчеты. ! Cto ,см |
Шриним.!Шаг вин4 Диаметр ша- ! <±о !та, t ! рика, d, |
||||
2,25 |
2,0 |
0,4 |
0,25 |
5,6 |
5,0 |
0,8 |
0,5 |
.2,75 |
2,5 |
0,5 |
0,3 |
|
|
1,2 |
0,7 |
3,25 |
3,0 |
0,6 |
0,35 |
6,5 |
6,0 |
0,8 |
0,5 |
|
|
1,0 |
0,6 |
|
|
1,2 |
0,7 |
3,75 |
3,5 |
0,6 |
0,35 |
7,5 |
7,0 |
1,0 |
0,6 |
|
|
1,0 |
0,6 |
|
|
1,6 |
1,0 |
4,25 |
4,0 |
0,6 |
0,35 |
8,5 |
8,0 |
1,0 |
0,6 |
|
|
1,0 |
'0,6 |
|
|
1,6 |
1,0 |
4,75 |
4,5 |
0,8 |
0,5 |
9,5 |
9,0 |
1,2 |
0,7 |
|
|
1.2 |
0,7 |
|
|
2,0 |
1,2 |
|
|
|
|
10,5 |
10,0 |
1,2 |
0,7 |
|
|
|
|
|
|
2,0 |
1,2 |
4<С
ДИНАМИКА
СТАНКОВ
Повышение
производительности станков связано с
увеличением частот вращения шпинделей,
нагрузок, действующих на элементы
станка. Вибрации, возникающие в станках,
ухудшают качество обрабатываемых
деталей. Поэтому возрастает значение
расчетов станков с учетом динамичности
их работы При этом решаются следующие
задачи:
Определение
динамических нагрузок для расчета
деталей станков.
. 2.
Определение областей безвибрационной
работы станка.
Определение
рационального режима переключения
ступеней скорости в автоматических
коробках скоростей по наименьшему
времени разгона и
Определение
частот собственных колебаний
Собственные
частоты крутильных колебаний системы
определяют для
выявления резонансных
частот методом "динамических
жесткостей", который
является
наиболее простым и эффективным среди
других методов. Он поз-
поляет
проводить частотный анализ сложной
системы при известных динами-
ческих
жесткостях ее составных частей /8/.
Динамическая жесткость к
это
отношение амплитудного значения
возмущающей силы к амплитудному
значению
перемещения. Если частота возбуждающей
силы равна нулю, то
динамическая
жесткость равна статической ( к
=С ).
Динамическая жест-
кость определяется
для заданной точки системы. При этом
для крайних
точек системы она равна
нулю: для точки, расположенной на опоре,
-
бесконечности, для массы, свободной
от закрепления, при поступательном
перемещении
-
г71 U)g
и -CfuJo
при
вращательном.
Рассмотрим
метод динамических жесткостей на
примере 3-массовых
систем (рис. 9.1).
Разрежим систему в некоторой точке
(например, "г") и
определим
динамические жесткости для правой и
левой частей.
Для
левой части
нагрузки.
С/
— У, еД?
Для
правой части
«е
-
О
; Kv
= - 7;
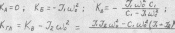
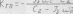
к
Рис.
9.1. Определение собственных частот
трехмассовой системы
Точки
пересечения графиков функций
■/*'
