Теория вероятностей

1. Элементы комбинаторики

Комбинаторика - раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных множеств.

Принцип умножения

Если объект А₁ может быть выбран k₁ способами, затем объект А₂ может быть выбран k₂ способами, затем после выбора объекта А₁ и объекта А₂ третий объект А₃ может быть выбран k₃ способами и т.д., включая m-й объект А_m, который может быть выбран k_m способами, то число способов выбора всех m объектов вместе равно k₁ ∙k₂ ∙k₃ ∙ ... ∙ k_{m .}

Пример. Сколько существует двузначных чисел, в которых циф­ра десятков и цифра единиц нечетные?

Решение. Для образования чисел используют только нечетные цифры, а именно 1, 3, 5, 7, 9. Значит, существует 5 способов поста­вить цифру на первое место. И для всех этих способов существует 5 способов поставить цифру на второе место, т.е. всего получается 5 ∙ 5 = 25 двузначных чисел, образованных только из нечетных цифр.

Рассмотрим некоторое множество различных предметов, облада­ющих общим свойством. Из этих предметов можно составлять группы с одним и тем же числом предметов в каждой группе, но отличаю­щиеся одна от другой или самими предметами или их порядком. Со­ставленные таким образом группы и называются соединениями.

Различают три вида соединений: размещения, сочетания, пере­становки.

Соединения, отличающиеся друг от друга составом элементов или их порядком, каждое из которых содержит m элементов, взятых из n различных элементов, называются размещениями из n элементов по m.

Задача о числе размещений. Сколькими способами можно выб­рать и разместить по m различным местам m из n разных предметов?

Количество всех таких способов принято обозначать 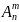(читается «число размещений из эн по эм»).

= n (n - l)(n - 2)...(n - m+1);

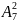= 7 ∙ 6 = 42.

Пример. Сколько всего семизначных телефонных номеров, в каждом из которых ни одна цифра не повторяется?

Решение. В задаче речь идет о выборе и размещении по семи различным местам семи из десяти различных цифр. Число телефонных номеров 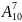=10∙ 9∙ 8∙ 7∙ 6∙ 5∙ 4 = 604800.

Соединения, каждое из которых содержит n различных элемен­тов, взятых в определенном порядке, называют перестановками из n элементов.

Задача о числе перестановок. Сколькими способами можно пере­ставить k различных предметов, расположенных на k разных мес­тах? Число всех таких способов принято обозначать 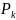(читается «чис­ло перестановок из k»).

= k!,

где k! = 1 ∙ 2 ∙ 3∙ … ∙k, 0! = 1.

Пример. Сколькими способами семь книг разных авторов мож­но расставить на полке в один ряд?

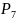
Решение. Эта задача о числе перестановок семи разных книг ‍ = ‍7! ‍= 1 ∙2 ∙3 ∙4 ∙5 ∙6 ∙7 = 5040. Следовательно, имеется 5040 способов осуществить расстановку книг.

Соединения, отличающиеся друг от друга по крайней мере од­ним элементом, каждое из которых содержит m элементов, взятых из n различных элементов, называются сочетаниями из n элементов по m.

Задача о числе сочетаний. Сколькими способами можно выбрать m из n различных предметов? Число всех таких способов принято обозначать читается «число сочетаний из эн по эм»).

,

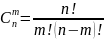
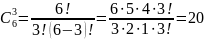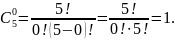
Пример. Сколькими способами читатель может выбрать две книги из пяти имеющихся?

Решение. Искомое число способов равно числу сочетаний из пяти книг по две. Поскольку 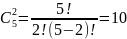, то указанную выборку читатель может осуществить десятью способами.

Пример. 12 человек играют в городки. Сколькими способами они могут набрать команду из четырех человек на соревнование?

Решение. Число способов выбрать четыре человека из 12 равно числу сочетаний из 12 по четыре, т. е. . Итак, 12 игроков могут набрать команду из четырех человек на соревнова­ние 495 способами.

Упражнения

1. Сколько различных трехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если цифры не повторяются?

Ответ: 100.

2. Сколько различных трехзначных чисел можно составить из цифр 0, 9, 8, 7, 6, 5, если цифры могут повторятся?

Ответ: 180.

3. Сколькими способами могут быть распределены три призо­вых места среди 12 соревнующихся?

Ответ: 1320.

4. Подбросили одновременно три разноцветные игральные ко­сти. Сколько существует возможных комбинаций выпавших очков?

Ответ: 216.

5. Составить различные размещения по два элемента из элемен­тов множества А={3, 5, 7} и подсчитать их число.

Ответ: 6.

6. Сколькими способами 3 награды (за I, II, III места) могут быть распределены между 9 участниками соревнований?

Ответ: 504.

7. Сколько имеется пятизначных чисел, у которых все цифры различны?

Ответ: 27216.

8. Сколькими способами можно составить трехцветный флаг с гремя горизонтальными полосами, если имеется материя 5 различ­ных цветов?

Ответ: 60.

9. Составить различные перестановки из элементов множества А={1; 2; 3} и подсчитать их число.

Ответ: 6.

10. Сколькими способами можно расставить в ряд 7 книг на книжной полке?

Ответ: 5040.

11. В комнате имеется 6 стульев. Сколькими способами можно разместить на них 6 гостей? 3 гостя?

Ответ: а) 720, б) 120.

12. Сколько всего перестановок можно получить из букв слова "кулич"?

Ответ: 120.

13. Составить различные сочетания по два из элементов множе­ства А = {9, 8, 7} и подсчитать их число.

Ответ: 3.

14. Сколькими способами можно распределить три билета в театр среди семи человек?

Ответ: 35.

15. Сколькими способами можно взять 3 книги из 7 имею­щихся?

Ответ: 35.

16. В классе 20 учеников. Сколькими способами можно разде­лить учащихся на две равные группы?

Ответ: 184756.

17. В ящике 10 деталей, среди которых 3 бракованные. Наудачу выбирают 5 деталей. Сколько существует способов извлечь 2 брако­ванные и 3 стандартные детали?

Ответ: 105.

18. В урне 12 белых шаров и 15 синих шаров. Сколькими спосо­бами можно выбрать из этой урны два шара одного цвета?

Ответ: 171.

Самостоятельная работа

1. Сколько существует двузначных чисел, имеющих обе чет­ные цифры?

Ответ: 20.

2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?

Ответ: 168.

3. Сколько шестизначных чисел, кратных 5, можно составить из цифр 0, 1,2, 3,4, 5 при условии, что в числе нет одинаковых цифр?

Ответ: 216.

4. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

Ответ: 900.

5. Сколько существует шестизначных чисел, которые делятся на 5'?

Ответ: 180000.

6. Сколькими способами можно выбрать три карандаша из шести имеющихся?

Ответ: 20.

7. В команде 9 спортсменов. Сколькими способами можно на­брать команду из семи человек на соревнование?

Ответ: 36.

8. В подразделении 30 солдат и 3 офицера. Сколько существует способов составить патруль, содержащий 3 солдат и одного офицера?

Ответ: 12180.

9. В вазе стоят 5 красных и 7 белых гвоздик. Сколькими спосо­бами можно выбрать из нее:

а) 3 гвоздики;

б) 5 гвоздик одного цвета;

в) 4 красных и 3 белых гвоздики?

Ответ: а) 220, б) 22, в) 175.

10. Из 20 рабочих нужно выбрать четырех человек для работы на определенном участке. Сколькими способами это можно сделать?

Ответ: 4845.

11. В группе 25 человек. Сколькими способами можно выбрать старосту и редактора газеты?

Ответ: 600.

12. Сколькими способами можно выбрать четырех человек на четыре различные должности из 9 кандидатов на эти должности?

Ответ: 3024.

13. Сколько четырехзначных чисел можно составить из цифр 1, 5, 6, 7, если цифры не повторяются?

Ответ: 24.

14. Сколькими способами можно разложить шесть различных писем по шести различным конвертам, если в каждый конверт кла­дется только одно письмо?

Ответ: 720.

15. Сколькими способами пять человек можно рассадить на одной скамейке?

Ответ: 120.

16. Студенты сдают 5 экзаменов, в том числе 2 экзамена по хи­мии. Сколькими способами можно распределить экзамены, но так, чтобы экзамены по химии

а) следовали один за другим?

б) не следовали один за другим?

Ответ: а) 48; б) 72.

Дополнительные задачи

1. Сколько всех четырехзначных чисел можно составить из цифр 1, ‍5,‍ 6, ‍7?

Ответ: 256.

2. Сколько пятизначных чисел, содержащих не менее трех по­парно различных цифр, можно составить из цифр 2, 4, 5, 7, 6, 8?

Ответ: 1920.

3. В цветочном киоске 7 видов цветов. Сколькими разными способами можно составить букет, содержащий 3 цветка?

Ответ: 35.

4. Из группы в 12 человек выбирают 4-х участников эстафеты 800x400x200x100. Сколькими способами можно расставить спорт­сменов на этих этапах?

Ответ: 11880.

5. Из двух математиков и десяти экономистов надо составить комиссию в составе восьми человек. Сколькими способами может быть составлена комиссия, если в нее должен входить хотя бы один математик?

Ответ: 450.

6. Сколькими способами можно расставить на книжной полке 5 томов произведений A.П. Чехова, располагая их:

а) в произвольном порядке?

б) так, чтобы I, II и III тома стояли рядом (в любом порядке);

Ответ: а) 120; б) 36.

7. В команде спортсменов 12 юношей и 10 девушек. Для учас­тия в соревнованиях выбирают 7 человек. Сколько существует спо­собов, при которых будут выбраны:

а) одни девушки?

б) 3 юноши и 4 девушки?

Ответ: а) 120; б) 46200.

8. Из цифр 1, 2, 3, 4, 5 составлены различные пятизначные числа, не содержащие одинаковых цифр. Сколько среди них таких, которые:

а) начинаются цифрой 3?

б) не начинаются цифрой 5?

в) начинаются с числа 54?

г) не начинаются с числа 54?

д) являются четными?

Ответ: а) 24; б) 96; в) 6; г) 114; д) 48.

10. В шахматном турнире сыграно 210 партий, причем каждый участник сыграл с каждым из остальных участников по одной партии. Сколько человек участвовало в турнире?

Ответ: 21.

11. У Нины - семь разных книг по математике, у Славы - девять разных книг по философии. Сколькими способами они могут обме­няться друг с другом пятью книгами?

Ответ: 2646.